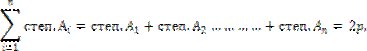Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7.3 Метрические характеристики графа.Содержание книги
Поиск на нашем сайте
Как от вершины А1 дойти до А5? Существуют следующие пути: 1. <A1,A4>,<A4, A5> 2. <A1, A2>,<A2, A4>,<A4, A5> 3. <A1, A3>,<A3, A4>,<A4, A5> 4. <A1, A4>,<A4, A2>,<A2, A1>,<A1, A3>,<A3, A4>,<A4, A5> 5. <A1, A4>,<A4,A2>,<A2, A1>,<A1, A4>,<A4, A5> - не является путем, т.к. ребро <A1, A4> встречается дважды. Путем от вершина А1 до вершины Аn называется такая последовательность ребер, ведущая от А1 до Аn, что любые два соседних ребра имеют общую вершину и ни одного ребра не встречается дважды. Путь, в котором начальные и конечные вершины совпадают называют циклом. Путь от вершины А1 до Аn называется простым, если он не проходит ни через одну из вершин графа более одного раза. Цикл называется простым, если он не проходит ни через одну из вершин графа более одного раза. Длиной пути (цикла) называется количество ребер его составляющих. Дан граф. Найти пути от А1 до А6 и определить их длину 1. <A1,A6>, d=1 2. <A1, A2>,<A2, A6>, d=2 3. <A1, A2>,<A2, A5>,<A5, A4>,<A4, A3>,<A3, A2>,<A2, A6>, d=6 4.
S(A1,A6)=1 S(A1, A7)=∞
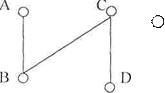
Вершины: 1. A и D – несвязные 2. A и Е – несвязные 3. А и В – связные 4. А и С – связные
Лабораторная работа № 3. Полный граф, его свойства. Теорема о сумме степеней вершин графа Цель работы: 1) Рассмотреть такую характеристику графа как вершина. 2) Изучить понятия полный граф. 3) Дать определение степени вершины. 4) Научиться определять четность вершины. Литература: 1) "Графы и их применение", Березина Л.Ю., М: Просвещение, 1979г. 2) "Теория графов. Алгоритмический подход", Кристофидес П. 3) "Применение теории графов в программировании", Евстигнеев В.А. - М.: Наука, 1985г. Порядок выполнения работы: I Разработать схему алгоритмов основной программы и подпрограмм. II Написать и отладить программу на языке Turbo Pascal. Задание: Граф задан матрицей смежности М = Для графа, заданного своей матрицей смежности, определить степени всех его вершин. Краткие теоретические сведения: Граф называется полным, если каждые две его вершины соединены одним и только одним ребром. Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
Е
Степ. А=1 Степ. В=2 Степ. С=2 Степ. D=l Стен. Е=0 Вершина называется нечетной, если её степень - число нечетное. Вершима называется четной, если её степень - число четное. Степень каждой вершины полного графа на единицу меньше числа его вершин. Теорема о сумме степеней графа В графе Г - сумма степеней всех его вершин, есть число четное, равное удвоенному числу его ребер, т.е.
где р - число ребер графа, n- число вершин. Содержание отчета: 1) Составление алгоритмов. 2) Написание программы на языке Turbo Pascal. 3) Отладка программы. Контрольные вопросы: 1) Что такое полный граф? 2) Дайте понятие степени вершины графа? 3) Какая вершина графа называется четной? 4) Какая вершина графа называется нечетной? 5) Сформулируйте теорему о сумме степеней вершин графа?
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.007 с.) |

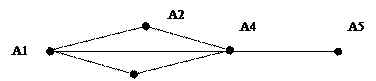 Пусть дан граф:
Пусть дан граф: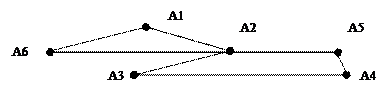 <A1, A2>,<A2, A3>,<A3, A4>,<A4, A5>,<A5, A2>,<A2, A6>, d=6
<A1, A2>,<A2, A3>,<A3, A4>,<A4, A5>,<A5, A2>,<A2, A6>, d=6 Расстоянием от вершины А до вершины В называется длина наименьшего пути, если не существует пути от А до В, то считают что расстояние равно бесконечности.
Расстоянием от вершины А до вершины В называется длина наименьшего пути, если не существует пути от А до В, то считают что расстояние равно бесконечности.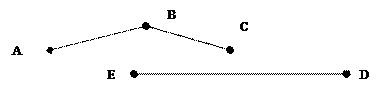 Вершины А и В называются связными, если не существует пути связывающего их.
Вершины А и В называются связными, если не существует пути связывающего их.