Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные положения прямой относительно плоскостей проекцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ.
Начертательная геометрия является тем разделом геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и алгоритмы решения задач. Лекции по начертательной геометрии предназначены для студентов заочников, обучающихся по сокращенной программе. В лекции, в разделе 1-го курса начертательной геометрии, рассматриваются в сокращенном виде. Важное прикладное значение этой дисциплины состоит в том, что она учит грамотно владеть выразительным техническим языком - языком чертежа, создавать чертежи и свободно читать их.
ЛЕКЦИЯ № 1
Точка. Проецирование точки на две плоскости проекций.
Основной курс начертательной геометрии – это курс метрических задач, теории теней и перспективы, проекции с числовыми отметками. Начертательная геометрия – наука молодая, основанная 200 лет назад Гаспаром Монж. Начертательная геометрия изучает методы и способы изображения пространственных фигур на плоском чертеже, алгоритмы решения позиционных метрических и конструктивных задач. Позиционные задачи на взаимную принадлежность и пересечение геометрических фигур. Метрические задачи на определение расстояний и натуральных величин геометрических фигур, конструктивные построения геометрических фигур и их образование на чертеже. Начертательная геометрия учит грамотно владеть выразительным техническим языком - языком чертежа, создавать чертежи и свободно читать их. Изучение н.г. способствует развитию пространственного воображения и навыков развития логического мышления. Изображение, полученное в результате центрального или параллельного проецирования, называется проекционным чертежом. Чертеж должен быть наглядным, Чертеж должен точно определять форму и положение изображаемого предмета, Изображение предмета должно быть удобным для чтения размеров, Процесс построения изображения должен быть простым.
Ортогональная система двух плоскостей проекций
Развернутый плоскостной чертеж – эпюр
Рис 1.2
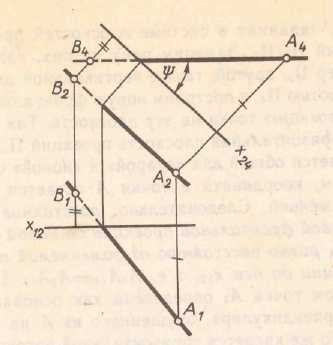
П1 – горизонтальная плоскость проекции, она бесконечна (см. рис 1.1.) П2 – фронтонная плоскость проекции П1 ^ П2 90о П3 – профильная плоскость Линии пересечения П1 П2 – ось х, П2 П3 – ось у, П1 П3 – ось z А1 – горизонтальная проекция (.) А (см.рис. 1.2.) А2 – фронтальная проекция (.) А (см.рис.1.2.) А3 – профильная проекция (.) А (см.рис.1.2.)
Любая точка, расположенная в пространстве имеет координаты. Координатами называются числа, которые ставят в соответствие точке для определения ее положения в пространстве. Координата – расстояние точки до плоскостей проекций.
Точки, расположенные на плоскости проекций
Рис 1.3
ЛЕКЦИЯ № 2 Прямая линия. Задание прямой линии. Проекции прямой
Положение прямой в пространстве определяется положением двух ее точек, так как через две точки можно провести только одну прямую. Это верно, но не полно, кроме двух точек положение прямой в пространстве можно определить двумя плоскостями, двумя проекциями, точкой и углами наклона к плоскостям проекций. Проекцией прямой на плоскости проекций является прямая.
Рис 2.1
Опустив перпендикуляр из точки А на П1 и П2 получим А1 и А2 рис 2.1
Рис 2.2 Проекции прямой АВ на эпюре рис.2.2 Следы прямой. Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций. см рис 2.7 Точка пересечения с плоскостью П1 называется горизонтальным следом М (М1М2М3). см рис 2.8 Точка пересечения с плоскостью П2 называется фронтальным следом N (N1N2N3). см рис 2.9 Точка пересечения с плоскостью П3 называется профильным следом Т (Т1Т2Т3).
Рис 2.7
Чтобы найти горизонтальный след прямой, т.е. точку пересечения прямой с горизонтальной плоскостью проекций П1 необходимо: 1. фронтальную проекцию прямой продолжить до пересечения с осью х – получим фронтальную проекцию горизонтального следа; 2. из точки пересечения с осью х опустить или восстановить перпендикуляр до пересечения с продолжением горизонтальной проекции прямой – получим горизонтальную проекцию горизонтального следа и сам след.
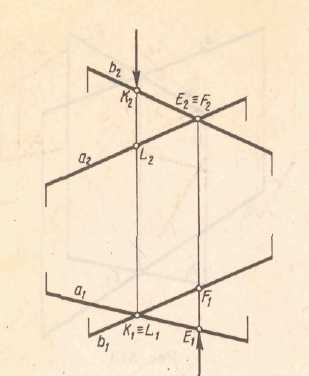
I. Параллельные прямые. Если прямые в пространстве параллельны, то их одноименные проекции так же параллельны. (см Рис 2.10)
Рис 2.10
II. Пересекающиеся прямые. Если две прямые в пространстве пересекаются, то их одноименные проекции тоже пересекаются. При этом точки пересечения их одноименных проекций должны быть расположены на одном перпендикуляре к оси х. (см рис 2.11)
Рис 2.11
III. Скрещивающиеся прямые.
Если прямые не параллельны и не пересекаются, то такие прямые называются скрещивающиеся прямые. Точки пересечения одноименных проекций не лежат на одном перпендикуляре к оси х. (см рис 2.12)
Проецирование прямого угла в натуральную величину Рис 2.12
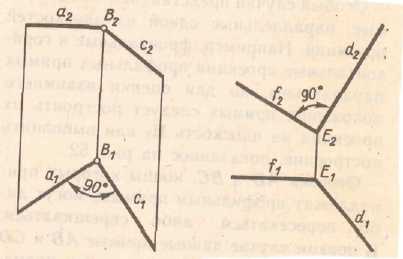
Если две прямые пересекаются под прямым углом, то проекции их не образуют прямой угол. Прямой угол на заданную плоскость проекций проецируется в виде прямого угла в том случае, когда одна из его сторон параллельна данной плоскости проекций, а вторая не перпендикулярна ей. (см рис 2.13)
Рис 2.13
ЛЕКЦИЯ № 3 Плоскость
Положение плоскости в пространстве определяется положениями задающих ее элементов. Плоскость может быть задана: 1) тремя точками, не лежащими на одной прямой
2) прямой и точкой, не лежащей на этой прямой
3) двумя пересекающимися прямыми
4) двумя параллельными прямыми
5) плоской фигурой
6) следами α1, α2, α3. След – линия пересечения плоскости с плоскостями проекций. Точка пересечения плоскости с осями проекций называется точкой схода следов.
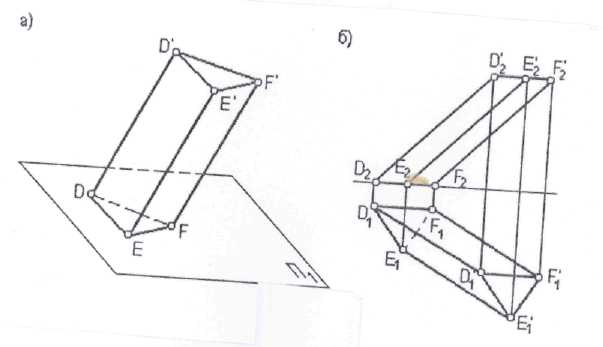
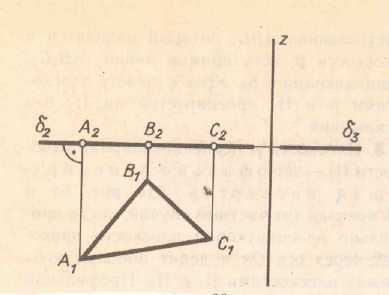
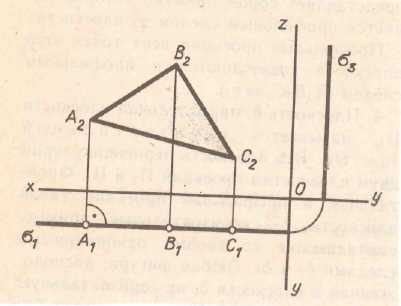
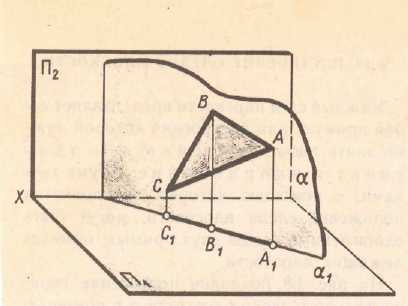
Различные положения плоскости относительно плоскостей проекций Плоскость АВС ║П1 (рис 3.1а), АВС║П2 (рис. 3.1б)
Плоскости проецирующие. Плоскости перпендикулярные плоскостям проекций
Основные аксиомы геометрии
Прямая принадлежит плоскости, если две точки этой прямой принадлежат той же плоскости. см. рис 3.3. Прямая L ║ прямой М.
Рис.3.3
Прямая принадлежит плоскости, если она имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости, см рис 3.3. Прямая L║прямой М
Рис 3.4
Точка принадлежит плоскости, если она расположена на прямой, лежащей в этой плоскости, см рис 3.5 (точка А)
Рис 3.5
Главные линии плоскости
Среди прямых линий, которые могут быть расположены в данной плоскости, особое место занимают прямые четырех направлений: 1. Горизонтали – прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций. Фронтальная проекция горизонтали, как линии параллельной плоскости П1 – горизонтальна (рис 3.6)
Рис. 3.6
2. Фронтали – прямые расположенные в плоскости и параллельные П2. рис. 3.7 3. Профильные прямые – прямые находящиеся в данной плоскости и параллельные П3. (рис. 3.8)
рис. 3.7
4. Линии наибольшего ската – прямые проведенные по плоскости перпендикулярно к горизонталям.
Рис 3.8
На любой плоскости можно провести бесчисленное множество главных линий. Все горизонтали плоскости параллельны между собой. Следы плоскости можно рассматривать как главные линии плоскости. (рис 3.9)
ЛЕКЦИЯ № 4 ЛЕКЦИЯ № 5 Способы преобразования чертежа.
Решение задач позиционного и главным образом метрического характера значительно облегчается когда данные элементы располагаются на прямых или на плоскостях частного положения. При решении метрических задач, которые связаны с определением истинных размеров изображаемых на эпюре фигур, могут встретиться трудности, если заданные проекции не подвергнуть специальным преобразованиям. Такими преобразованиями являются: 1) способ замены плоскостей проекций; 2) способ вращения; 3) способ плоскопараллельного перемещения. В этой лекции мы рассмотрим эти способы, которые дадут возможность переходить от общих положений прямых и плоских фигур к частным в системе плоскостей П1 и П2. Способ замены плоскостей проекций заключается в том, что положение точек линий, плоских фигур поверхностей в пространстве остается неизменным, а система плоскостей проекций П1П2 дополняется новыми плоскостями проекций так, чтобы получаемые на них проекции обеспечивали рациональное решение, но каждая новая система плоскостей проекций должна быть ортогональной. В некоторых случаях для решения задачи достаточно введение одной дополнительной плоскости проекций. Обычно вводится новая плоскость проекций перпендикулярно горизонтальной плоскости проекций при этом сама плоскость проекций является горизонтально-проецирующей или вводится новая плоскость проекций перпендикулярная фронтальной плоскости проекций при этом сама плоскость проекций является фронтально-проецирующей плоскостью. Если введение одной дополнительной плоскости проекций недостаточной для решения задачи, то вводят дополнительные плоскости проекций, но уже к измененной системе плоскостей проекций. Можно представить переход от одной системы плоскостей проекций к последующим системам в следующем виде:
Рассмотрим некоторые примеры.
Определим натуральную величину отрезка прямой общего положения. Решение: нам известно, что если отрезок прямой параллелен какой-либо плоскости проекций, то на данную плоскость проекций этот отрезок проецируется в натуральную величину. Это положение позволяет нам ввести дополнительную плоскость проекций таким образом, что она будет перпендикулярна горизонтальной плоскости проекций и в тоже время параллельна самому отрезку. На новую плоскость проекций заданный отрезок спроецируется в натуральную величину. Рис.5.1 (а) При решении данной задачи можно было ввести дополнительную плоскость фронтально-проецирующую и параллельную самому отрезку и получить тот же самый конечный результат. Рис 5.1 (б)
Рис 5.1
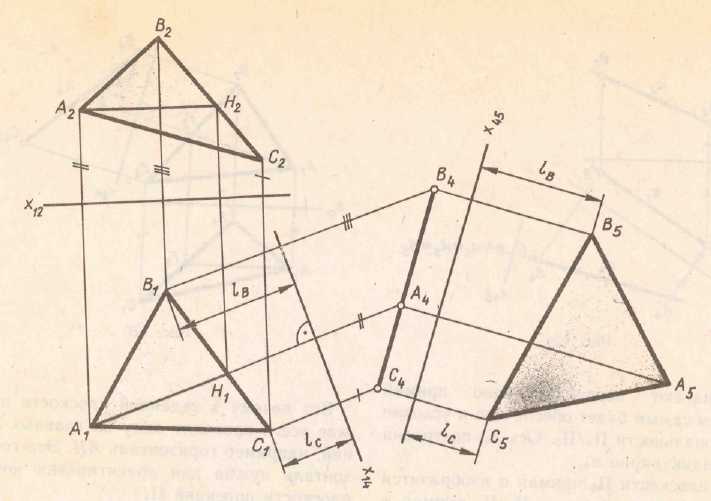
Рассмотрим еще один пример. Введение дополнительной плоскости проекций дает возможность преобразовать чертеж так, что плоскость общего положения заданная в системе
а)
б) Рис.5.2
Способ вращения
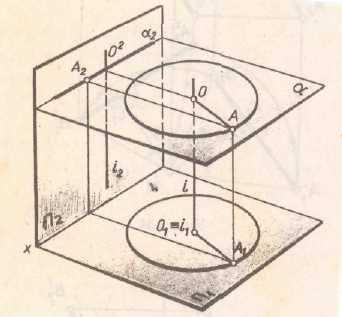
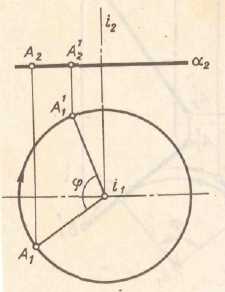
Способ вращения заключается в том, что положение данной геометрической фигуры относительно неподвижных плоскостей проекций изменяют посредством поворота ее вокруг некоторой оси. Для осуществления этого способа необходимо задать некоторую неподвижную прямую – ось вращения. Каждая точка вращаемого объекта перемещается в плоскости перпендикулярной к оси вращения. При этом любая точка объекта будет перемещаться по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра вращения (радиус вращения). Ось вращения может быть задана или выбрана. Если ось вращения перпендикулярна к плоскости П2, то плоскость в которой происходит вращение точки А параллельна плоскости П2. Следовательно траектория движения точки проецируется на П2 без искажения, а на П1 – в виде отрезка прямой. Рис 5.3
Рис 5.3 Вращение точки вокруг заданной оси перпендикулярно к плоскости проекций. Пусть точка А вращается вокруг оси перпендикулярной к плоскости П1. Через точку А проведена плоскость перпендикулярная к оси вращения и следовательно параллельна П1. При вращении точка А описывает в плоскости окружность радиуса R. Величина радиуса выражается длинной перпендикуляра проведенного из точки А на ось. Окружность описанная в пространстве точкой А проецируется на П1 без искажения, а на П2 – в виде отрезка прямой. Рис 5.4 (а) на рис 5.4 (б) на П1- в виде отрезка прямой
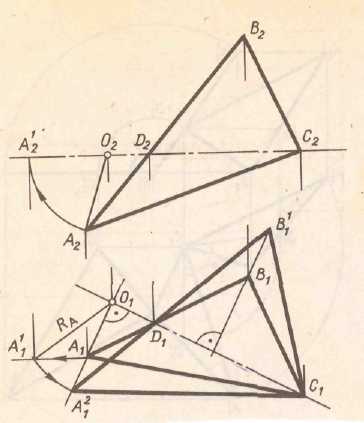
Рис 5.4 Требуется определить натуральную величину отрезка прямой общего положения способом вращения. При решении данной задачи ось вращения удобно выбрать проходящей через один из концов отрезка. Построение при этом упростится, так как точка через которую проходит ось будет неподвижной и для поворота отрезка надо построить новое положение проекций точки одной точки – другого конца прямой. Рис.5.5(а) Если выбрать ось перпендикулярную П1 и провести ее через точку В, то нужно поворачивать точку А до тех пор пока отрезок не займет положение параллельное фронтальной плоскости проекций. Рис 5.5 (б)
Рис 5.5
Способ вращения в дальнейшем будем использовать при построении разверток различных поверхностей. И в заключении рассмотри применение способа вращения без указания на чертеже осей вращения перпендикулярных к плоскости П1. Этот случай вращения называют способ плоскопараллельного перемещения и заключается он в том, что данный элемент в пространстве перемещается таким образом, что все точки его всё время находятся во взаимно-параллельных плоскостях. На этом эпюре перемещение осуществляют параллельно плоскостям проекций П1 или П2, когда каждая точка фигуры движется в плоскостях уровня. Рис 5.6
Рис 5.6
Этот способ имеет преимущество перед вращением. Упрощается построение, не происходит наложений одной проекции на другую.
ЛЕКЦИЯ № 6 Особые точки кривой
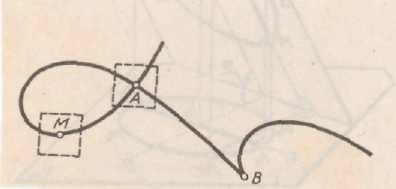
Обыкновенной точкой кривой называют такую точку М, которую можно заключить в прямоугольник (хотя бы очень малый) так, что попавшая в него часть кривой является простым отрезком. Рис.6.1
Рис.6. 1
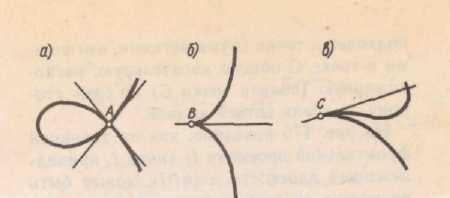
Все другие точки являются особыми узловая точка А или точка самопересечения. В этой точке кривая имеет две различные касательные. Точка В (точка возврата) первого рода, в которой кривая подходит к точке двумя ветвями, имеющими в точке В общую касательную. Точка С (точка возврата) второго рода, в которой кривая подходит к точке двумя ветвями, имеющими в точке С общую касательную, расположенную в близи точки С, по одну сторону от обеих ветвей. Рис. 6.2 а,б,в
Рис. 6.2 Пространственные кривые
Кривая линия называется пространственной, если она всеми своими точками не лежит в одной плоскости. К пространственным кривым линиям относятся цилиндрическая и коническая винтовые линии.
Цилиндрическая винтовая линия.
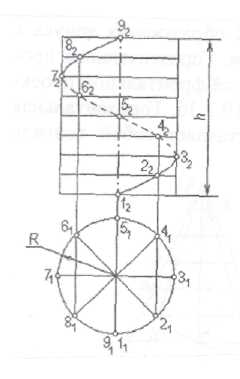
Цилиндрической винтовой линией называется траектория точки, движущейся по образующей прямого кругового цилиндра, которая, в свою очередь, вращается вокруг оси цилиндра. Расстояние, на которое перемещается точка по образующей за один полный её оборот, называется шагом винтовой линии. Ось цилиндра называется осью винтовой линии. Радиус основания цилиндра называется радиусом винтовой линии. Рассмотрим построение цилиндрической винтовой линии, перпендикулярной к плоскости П1 с шагом h и радиусом R. Такая винтовая линия на плоскости П1 изобразится в виде окружности радиуса R. Чтобы построить фронтальную проекцию винтовой линии, следует разделить её горизонтальную проекцию на несколько равных частей. В данном случае разделим окружность на 8 частей. На такое же количество частей делим фронтальную проекцию. В данном случае высота фронтальной проекции является шагом винтовой линии. Построение винтовой линии на рис.6.3 начато сточки 1 (11,12). При повороте точки на одну восьмую (1/8) часть дуги окружности она соответственно переместится по высоте вдоль оси винтовой линии на 1/8 часть шага (точки 21 и 22). При повороте точки на две восьмых дуги окружности точка переместится на две восьмых (2/8) высоты шага (точки 31 и 32) и т.д. (рис.3).
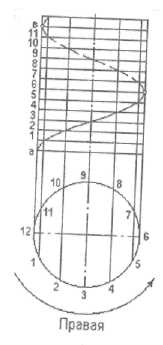
Рис. 6.3 Соединив фронтальные проекции точек 12, 22, 32 и т.д. плавной кривой, получим фронтальную проекцию цилиндрической винтовой линии. Цилиндрическая поверхность при построении винтовой считается непрозрачной. Различают правую и левую винтовую линии. Правой называют винтовую линию, когда точки при подъёме вращаются против часовой стрелки, а её участок на передней части цилиндра имеет подъём слева направо. У левой винтовой линии точка вращается по часовой стрелке, а подъём кривой линии на передней части цилиндра справа налево (рис.6.4 а, б).
а) б) Рис. 6.4
Коническая винтовая линия.
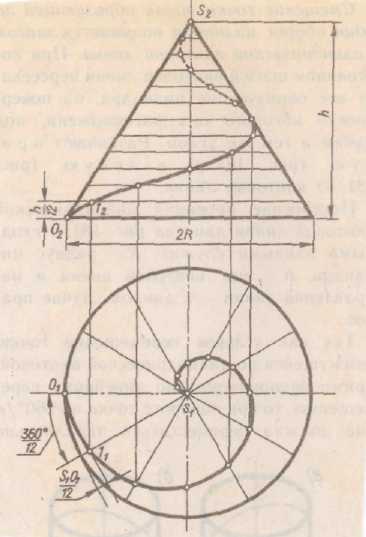
Такую линию описывает точка, которая движется по какой-нибудь образующей прямого кругового конуса, вращающегося в то же время около своей оси так, что путь проходимый точкой по образующей все время пропорционален углу поворота конуса. Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Особенность построения горизонтальной проекции конической винтовой линии состоит в том, что горизонтальная проекция движущейся точки определяется с учетом двух движений: вращательного — вместе с образующей и поступательного — вдоль образующей. Так, при построении точки 1 горизонтальная проекция образующей конуса SO была повернута на 360°/12, а точка перемещена по ней на l/12 длины SO. В такой же последовательности построены и остальные точки. Горизонтальная проекция конической винтовой линии представляет собой спираль Архимеда. Фронтальная проекция каждой точки винтовой линии определяется пересечением фронтальных проекций параллелей конуса, плоскости которых смещены одна относительно другой на расстояние, равное h /12, и линий проекционной связи.
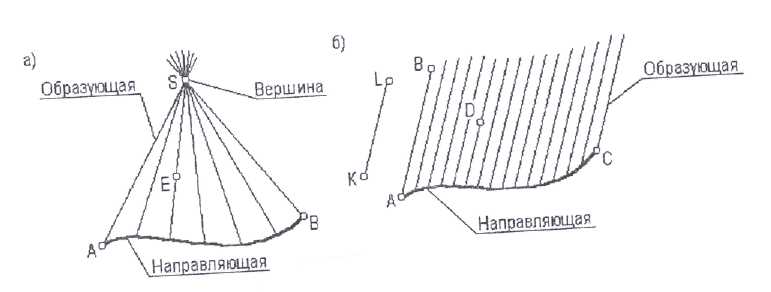
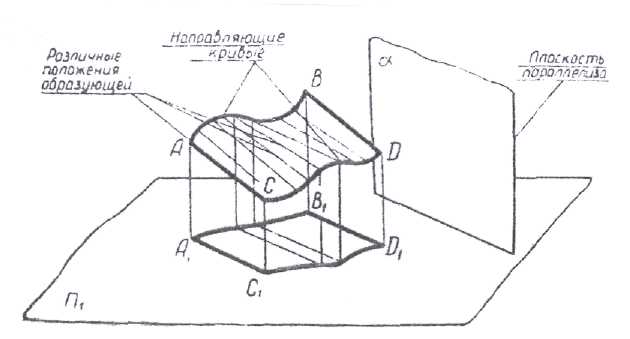
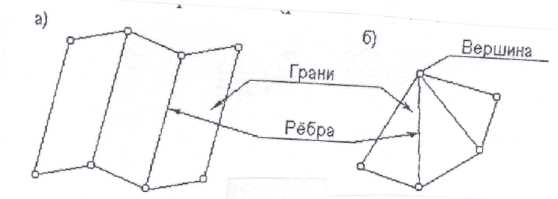
Рис. 6.5 Всякая правильная кривая поверхность представляет собой непрерывную совокупность последовательных положений прямой или кривой линии, движущейся в пространстве по определённому закону. Линия, образующая своим движением поверхность, называется образующей поверхности. Линия, по которой движется образующая, называется направляющей поверхности. На рисунке 6 а, б дан пример образования конической и цилиндрической поверхности.
Рис. 6.6 Рис. 6.6 Чертёж поверхности представляет собой проекцию очерка поверхности. Очерком поверхности называется проекция видимого контура поверхности относительно данной плоскости проекции. Контуром видимости поверхности является линия касания проецирующих лучей, огибающих (обёртывающих) данную поверхность при изображении её на плоскости проекций. На рисунке 6.7 дано построение очерковых образующих цилиндра на фронтальную и горизонтальную плоскость проекций.
Рис. 6.7
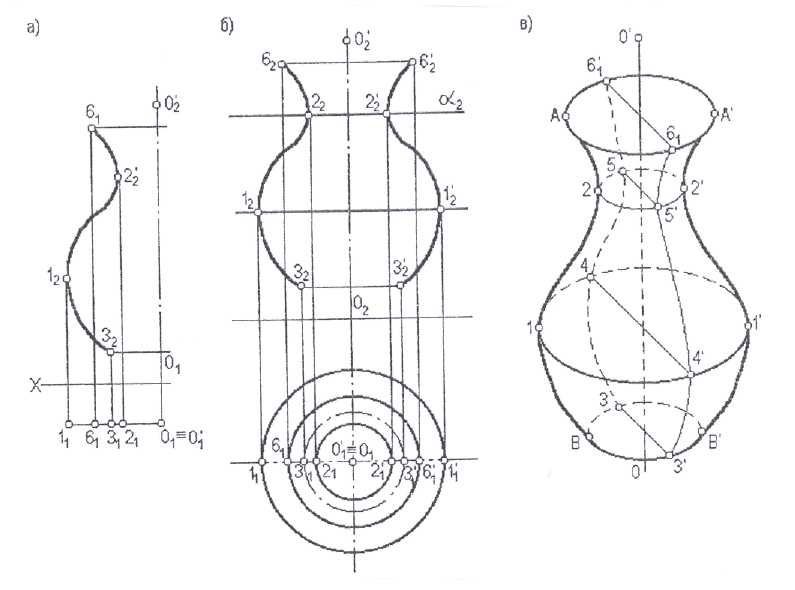
В зависимости от вида образующих, все кривые поверхности можно разделить на два класса: 1.Поверхности с прямолинейными образующими - это линейчатые поверхности. 2.Поверхности с криволинейными образующими. Линейчатые поверхности, в свою очередь, делятся на развёртываемые и неразвёртываемые. Развёртываемой называется поверхность, если её без складок и разрывов можно совместить с плоскостью. У развёртываемых поверхностей смежные образующие параллельны друг другу или пересекаются друг с другом. У поверхностей неразвёртываемых смежные прямолинейные образующие не параллельны друг другу и не пересекаются. Все поверхности с криволинейными образующими неразвёртываемые. Из общей массы поверхностей выделяется особый класс поверхностей, которые называются поверхностями вращения. Поверхности вращения образуются вращением какой-нибудь образующей прямой или кривой вокруг неподвижной прямой, которая является осью вращения. При вращении кривой 6, 2, 1, 3 вокруг оси ОО (рис.6.8а) образуется поверхность вращения. На рис.6.8б она представлена ортогональным чертежом, а на рис.6.8 г дано её наглядное изображение.
Рис. 6.8 Сечение поверхности вращения плоскостью, перпендикулярной оси вращения, представляет собой окружность. Все такие окружности называются параллелями поверхности. Параллель наибольшего диаметра называется экватором, меньшего диаметра - горлом поверхности. На рис.6.8б окружность 1-1 - экватор, окружность 2-2 - горло поверхности. Следы секущих плоскостей α2, β2 перпендикулярны оси вращения поверхности. Плоскость, проходящая через ось поверхности вращения, называется меридиональной плоскостью, а контур сечения поверхности такой плоскости - меридианом. Все меридианы представляют собой кривые, равные друг другу. Рассмотрим образование некоторых наиболее часто встречающихся в инженерной практике поверхностей. Цилиндрическая поверхность представляет собой поверхность, образованную движением прямой линии по некоторой кривой линии. Причём прямая во всех своих положениях остаётся параллельной некоторому постоянному направлению (рис.6.9).
Рис.6. 9
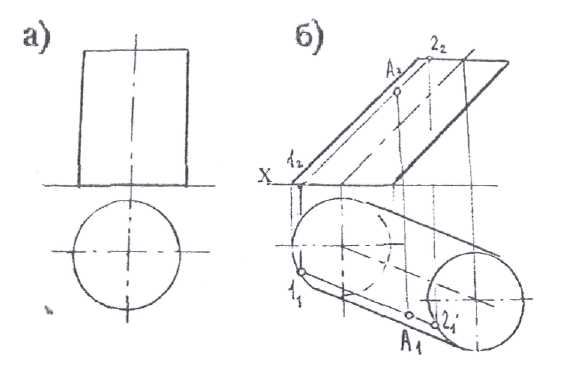
Если точка лежит на цилиндрической поверхности, то она должна лежать на образующей этой поверхности. Замкнутая цилиндрическая поверхность, заключённая между двумя параллельными плоскостями образует геометрическое тело - цилиндр. На рис 6.9а изображён прямой цилиндр, на рис.6.9б - наклонный. На рис.6.9б показано положение точки на поверхности цилиндра. Коническая поверхность представляет собой поверхность, образованную движением прямой линии по некоторой направляющей. В данном случае направляющей является окружность. Причём прямая во всех положениях проходит через одну и ту же точку, называемую вершиной (рис.6.10). Часть замкнутой конической поверхности, заключённой между её вершиной и плоскостью любого направления, образует геометрическое тело - конус. На рис. 6.10 а, б дано изображение прямого и наклонного конуса и определение положения точки на их поверхностях.
Рис. 6.10
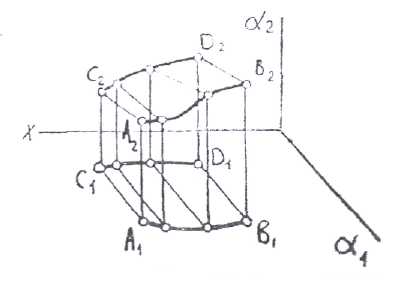
Цилиндроид - поверхность, образованная движением прямой линии по двум не лежащим в одной плоскости направляющим - кривым линиям. При этом прямая во всех положениях остаётся параллельной некоторой плоскости -плоскости параллелизма. На рис.6.11а дано наглядное изображение цилиндроида. На рис.6.11б изображён цилиндроид в ортогональной проекции.
б) Рис. 6.12
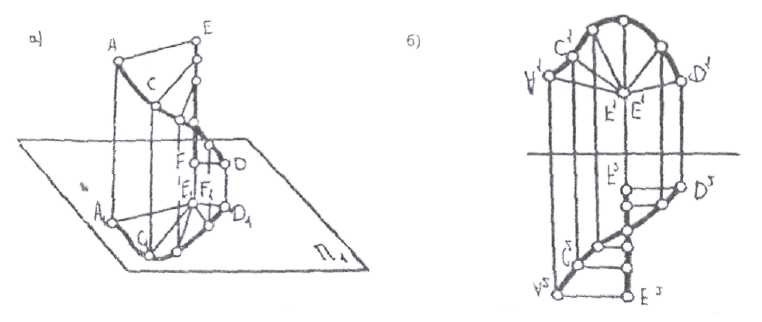
Коноид - линейчатая поверхность, у которой одна направляющая является кривой линией, а вторая - прямой. Образующая во всех положениях параллельна некоторой плоскости параллелизма (рис.12 а, б).
Рис. 6.12
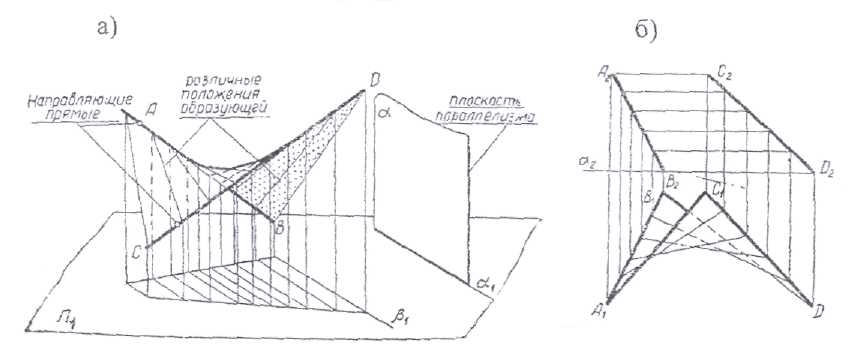
Косая плоскость (гиперболический параболоид) - частный случай цилиндроида и представляет собой поверхность, образованную движением прямолинейной образующей параллельно плоскости параллелизма по двум скрещивающимся направляющим прямым. Это АВ и CD. За плоскость параллелизма принята горизонтальная плоскость П1, образующая АС || П1 (рис.6. 13). Косая плоскость относится к линейчатым поверхностям. Она образуется движением прямой линии. Однако для этой поверхности образующей может быть и кривая линия, например, парабола. Если эту поверхность пересечь плоскостью, параллельной плоскости П1, то в сечении получится гипербола. Поэтому косую плоскость также называют гиперболическим параболоидом.
Рис.6. 13
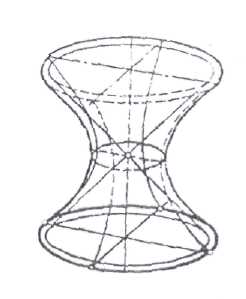
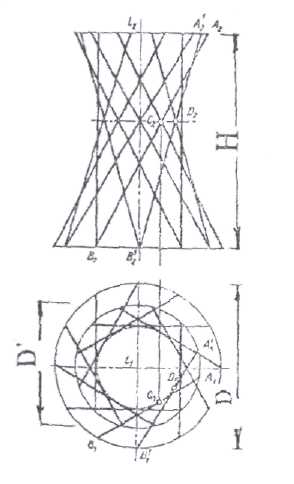
Гиперболоид вращения. Существуют два вида гиперболоида: однополостный и двуполостный. Первый получается при вращении гиперболы вокруг её мнимой оси (рис.6.14а). Поверхность однополостного гиперболоида может быть образована и вращением прямой линии. Это поверхность дважды линейчатая, т.е. через каждую точку однополостного гиперболоида проходят две и только две его прямолинейные образующие. Проекции однополостного гиперболоида строятся следующим образом (рис.6.14б). Пусть ось i расположена перпендикулярно плоскости П1. Когда образующая АВ вращается вокруг оси i, каждая точка прямой перемещается в пространстве по окружности (параллели), плоскость которой перпендикулярна оси i. Таким образом, на плоскости П1 эта окружность проецируется без искажения, а на плоскость П2 - в виде горизонтальной прямой. Ближайшая к оси вращения точка С образующей опишет окружность минимального радиуса. Это будет окружность горла. Горизонтальные проекции всех образующих должны касаться проекции окружности горла. Таким образом, каждое последующее положение прямолинейной образующей можно получать проведением касательных к проекции окружности горла. На рис.6.14б эта окружность разделена на двенадцать частей. К проекции этой окружности в точке D1 проведена касательная A1'B1', a горизонтальная проекция образующей повёрнута на 30°. Фронтальная проекция этой касательной определяется точками A2'B2', каждая из которых расположена в плоскости своей параллели. Остальные образующие строятся аналогично. Форма поверхности гиперболоида зависит от следующих параметров: D' и D, D' и Н, а также и от диаметра горла поверхности.
Рис.6. 14
ЛЕКЦИЯ № 7 Гранные поверхности Многогранник – это конечная часть пространства, ограниченная отсеками пересекающихся плоскостей. Совокупность отсеков образует гранную поверхность многогранника. Отсеки плоскостей называются гранями, а линии их пересечения ребрами. Ребра пересекаются в точках, называемых вершинами. Гранная поверхность называется выпуклой, если она целиком лежит по одну сторону от плоскости любой своей грани. Если гранями многоранника служат равные правильные многоугольники, а многогранные углы при вершинах равны, то такой многогранник правильный. Существует пять правильных многогранников: тетраэдр – четырехгарнник; гексаэдр – куб; октаэдр – восмигранник; додекаэдр – двенадцатигранник; икосаэдр – двадцатигранник. Определителем многогранника называется совокупность условий необходимых и достаточных для его однозначного задания.
Рис.7.1
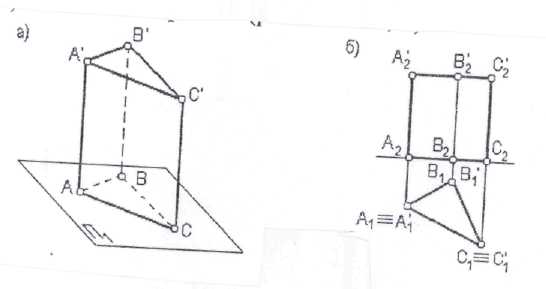
Наиболее распространенными видами многогранников являются призмы и пирамиды. Призма, у которой боковые грани перпендикулярны плоскости основания называется прямой (рис. 7. 2 аб).
Рис. 7.2
Если боковые грани призмы не перпендикулярны плоскости основания, то такая призма называется наклонной (рис.7.3 а, б).
Рис. 7.3
Многогранник, у которого основание представляет собой многоугольник, а боковые грани - треугольники, сходящиеся в одной точке - вершине, называется пирамидой. Если высота пирамиды проходит через центр тяжести основания, то такая пирамида называется прямой. При всех других случаях пирамида будет наклонной (рис 7.4).
Рис. 7.4
На ортогональных чертежах каждый многогранник должен быть изображён двумя проекциями всех рёбер и вершин. Если точка лежит на поверхности многогранника, то она располагается либо на ребре, либо на грани этого многогранника (рис.7.5 а, б, в). Построение точки на ребре многогранника выполняется также, как построение точки на прямой (рис.7.5а). Проекции точки на поверхности грани многогранника находятся так же, как проекции точки на плоскости. Сначала через проекцию точки проводится прямая, заведомо лежащая в плоскости грани. Затем эта проекция прямой строится на другой проекции грани. Далее на этой проекции прямой строится проекция точки (рис.7.5 б, в).
Рис.7. 5
ЛЕКЦИЯ № 8 ВВЕДЕНИЕ.
Начертательная геометрия является тем разделом геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и алгоритмы решения задач. Лекции по начертательной геометрии предназначены для студентов заочников, обучающихся по сокращенной программе. В лекции, в разделе 1-го курса начертательной геометрии, рассматриваются в сокращенном виде. Важное прикладное значение этой дисциплины состоит в том, что она учит грамотно владеть выразительным техническим языком - языком чертежа, создавать чертежи и свободно читать их.
ЛЕКЦИЯ № 1
Точка. Проецирование точки на две плоскости проекций.
Основной курс начертательной геометрии – это курс метрических задач, теории теней и перспективы, проекции с числовыми отметками. Начертательная геометрия – наука молодая, основанная 200 лет назад Гаспаром Монж. Начертательная геометрия изучает методы и способы изображения пространственных фигур на плоском чертеже, алгоритмы решения позиционных метрических и конструктивных задач. Позиционные задачи на взаимную принадлежность и пересечение геометрических фигур. Метрические задачи на определение расстояний и натуральных величин геометрических фигур, конструктивные построения геометрических фигур и их образование на чертеже. Начертательная геометрия учит грамотно владеть выразительным техническим языком - языком чертежа, создавать чертежи и свободно читать их. Изучение н.г. способствует развитию пространственного воображения и навыков развития логического мышления. Изображение,
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.013 с.) |

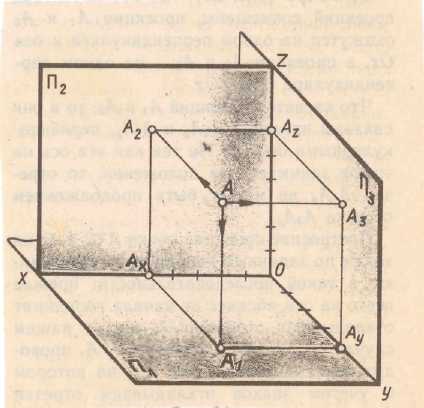 Проецирование точки на плоскости проекции
Проецирование точки на плоскости проекции
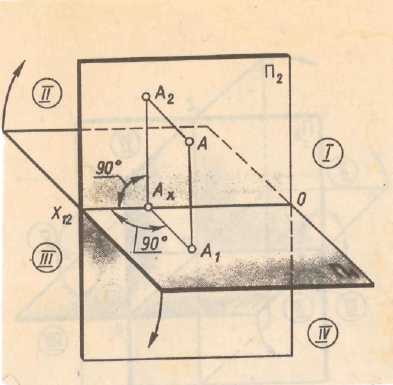 Совмещение плоской проекций
в развернутый чертеж
Рис 1.1.
Совмещение плоской проекций
в развернутый чертеж
Рис 1.1.
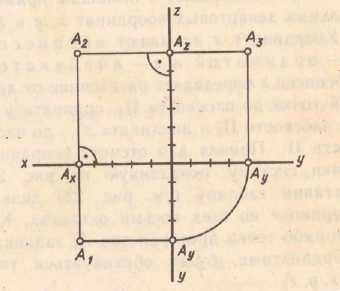
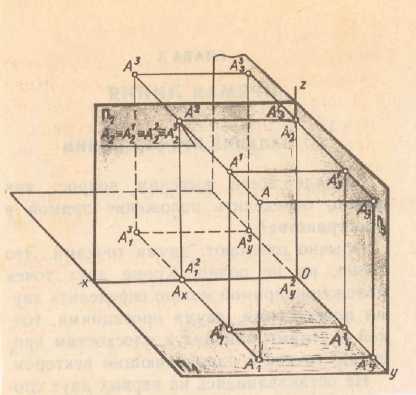 а) наглядное изображение точек А и А1
а) наглядное изображение точек А и А1
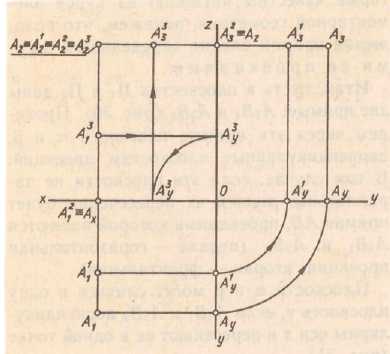 б) Расположение проекций точек
А и А1 на эпюре
б) Расположение проекций точек
А и А1 на эпюре

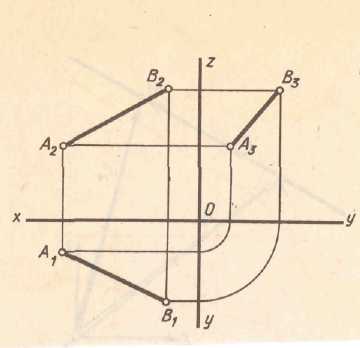
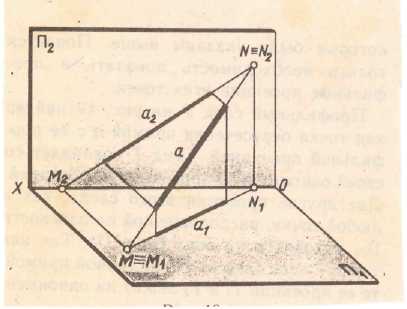
 Рис 2.8
Рис 2.8
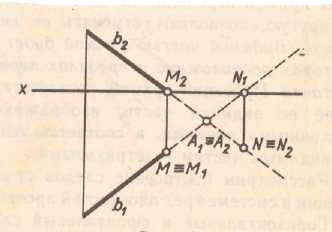 Рис 2.9
Рис 2.9



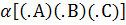 ;
;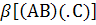 ;
;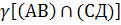 ;
;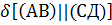 ;
;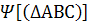 ;
;
 б)
Рис 3.1
б)
Рис 3.1
 а)
а)
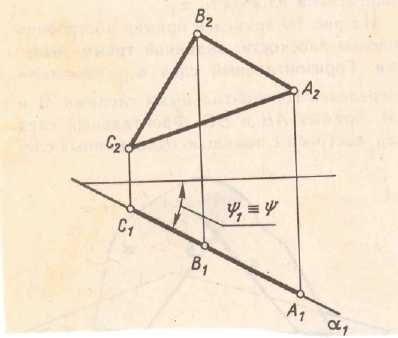
 б)
б)
 Рис.3.2
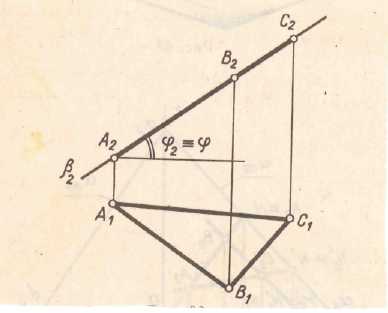
На рис. 3.2 а плоскость ┴ П2, на рис 3.2 (б) плоскость ┴ П1, на рис 3.2 (в) плоскость ┴П3
Свойства проецирующих плоскостей:
1) проекции точек и линий, лежащих в этих плоскостях, будут находиться на той проекции, где плоскость изображается прямой линией;
2) углы наклона проецирующих плоскостей к плоскостям проекций проецируются в натуральную величину.
Рис.3.2
На рис. 3.2 а плоскость ┴ П2, на рис 3.2 (б) плоскость ┴ П1, на рис 3.2 (в) плоскость ┴П3
Свойства проецирующих плоскостей:
1) проекции точек и линий, лежащих в этих плоскостях, будут находиться на той проекции, где плоскость изображается прямой линией;
2) углы наклона проецирующих плоскостей к плоскостям проекций проецируются в натуральную величину.

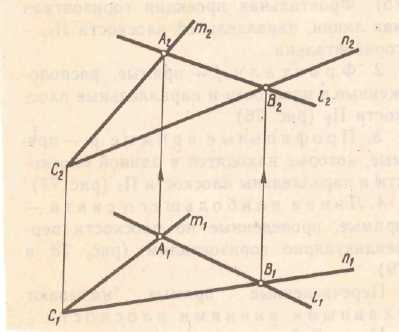
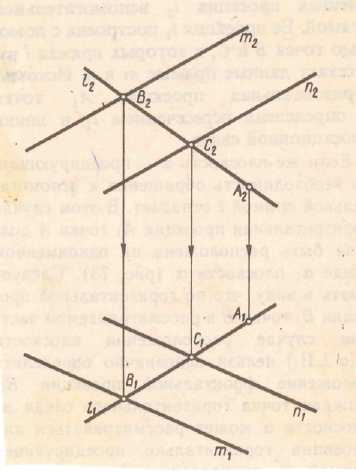
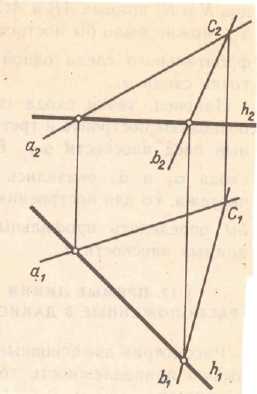

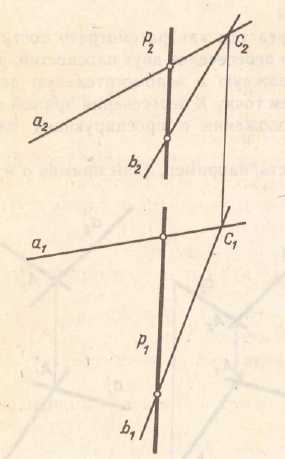
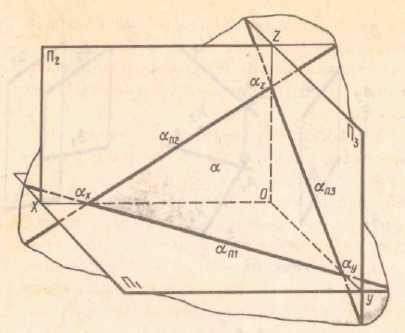

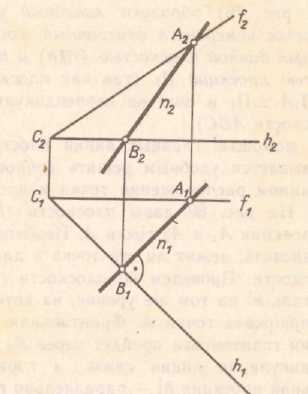 Рис. 3.9
Рис. 3.9
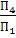
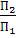
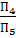

 а)
а)
 б)
б)
 в)
в)
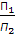 становится частного положения в новой системе плоскостей проекций. Рис.5.2(а). На рис 5.2 (б) второй определена натуральная величина треугольника АВС
становится частного положения в новой системе плоскостей проекций. Рис.5.2(а). На рис 5.2 (б) второй определена натуральная величина треугольника АВС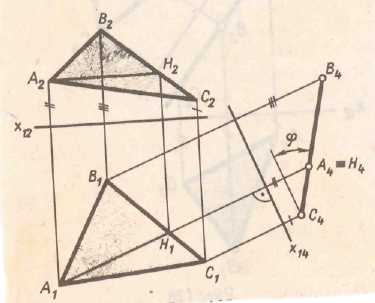
 а)
а)
 б)
б)
 а)
а)
 б)
б)