Пересечение призмы и пирамиды

 

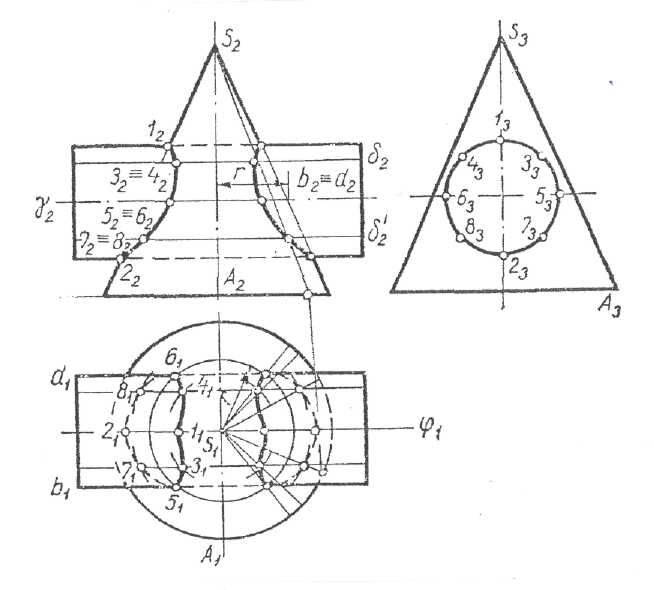
Для определения точек линии пересечения используются гори­зонтально-проецирующие плоскости α, β, γ. Рёбра ЕЕ' и FF' в пересе­чении не участвуют. Определение точек линии пересечения сводится (как и в ранее рассматриваемых примерах) к определению точки пере­сечения ребра (как прямой) с плоскостью грани фигуры. В данном случае, так как два ребра призмы в пересечении не участвуют, следует определить точки пересечения ребра DD' с гранями ASB и BSC (рис.8.3). Для этого заключаем ребро DD' в горизонтально-проецирующую плоскость α. Затем находим линию пересечения вспомогательной плоскости α с гранью ASB - это будет линия КМ - и с гранью BSC - это будет линия LN.

На горизонтальной проекции они совпадут со следом плоскости α₁. На фронтальной проекции точка 1₂ пересечения D₂D₂' с К₂М₂ и точка 2₂ пересечения D₂D₂' с L₂M₂ будут являться точками, принадлежащими линии пере­сечения. Чтобы определить точки пересечения ребра пи­рамиды SA с гранями призмы FF', D₁D' и D₁D', EE', заключаем ребро SA в горизонтально-проецирующую плоскость β. Находим линию пересечения её PQ с гранью FF', DD' и ли­нию пересечения RQ с гранью DD', ЕЕ'. Точки пересечения 3, 4 с этими линиями пересе­чения дадут нам искомые точ­ки. Все остальные построения аналогичны разобранным и понятны из чертежа.

 

Рис. 8.3

 

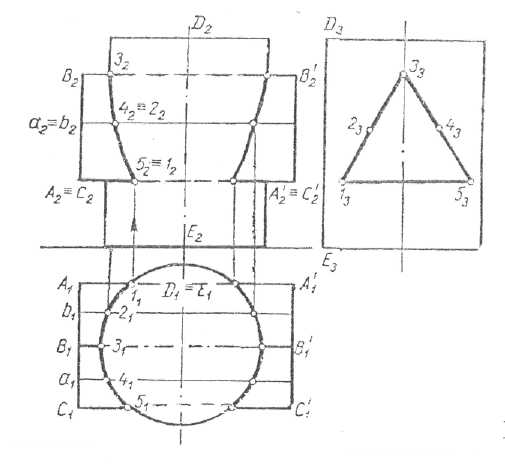
На рис 8.4 приведён пример пересечения призмы с цилиндром. Все построения понятны из чертежа.

 

Рис.8. 4

 

На рис.8.5 приведён пример пересечения конуса с цилин­дром. Линия пересечения построена с помощью плоскостей посред­ников. Последовательность построения понятна из чертежа. Здесь представлено полное пересечение.

 

Рис.8.5

 

На рис.8.6 даётся пример пересечения цилиндра с конусом. Как и в предыдущем случае, линия пересечения определяется с помо­щью плоскостей-посредников. Линия пересечения здесь представляет одну замкнутую линию. Это будет частичное пересечение. Построе­ние линии пересечения понятно из чертежа.

 

Рис.8.6

 

На рис.8.6 дается построение линии пересечения цилиндра с шаром. Построение точек линии пересечения определяется с помо­щью вспомогательных плоскостей частного положения.

Это плоскости дважды проецирующие - горизонтальные. Такая плоскость пересекает обе поверхности по окружности. Сначала нахо­дим эти точки на горизонтальной проекции, а затем проецируем на фронтальный след проецирующей плоскости. Построения понятны из чертежа.

В задаче, приведённой на рис.8.7 и 8.8 для определение точек линии пересечения в основном используются плоскости, параллель­ные плоскости П₂ - фронтальные плоскости. Эти плоскости пересека­ют поверхность шара по окружности, а поверхность цилиндра по образующим. На их пересечении получаем точки 1, 2, 5, 6 и др. Низшую точку А и высшую точку В находим на пересечении с поверхностью шара тех образующих цилиндра, которые расположены в горизон­тально-проецирующей плоскости β, проходящей через ось цилиндра и центр шара. Остальные построения понятны из чертежа.

 

Рис. 8.7	Рис. 8.8

 

Построение линии пересечения конуса с на­клонным цилиндром

 

Оси вращения этих поверхностей пересекают­ся и параллельны плоско­сти П₂. Следовательно, для определения линии пере­сечения (линии перехода) можно использовать сфе­рические посредники. Все построения выполняются на основании приёмов, разобранных ранее и по­нятны из чертежа (рис.8.9).

 

Рис.8.9

 

Частные примеры пересечения поверхностей вращения второго порядка

В том случае, когда две пересекающиеся поверхности второго порядка (цилиндр и конус) касаются третьей по­верхности второго порядка (в данном случае шара), имеет место следующее по­ложение. Две поверхности второго порядка пересекают­ся по двум плоским, если эти поверхности описаны около третьей поверхности второго порядка или вписаны в неё (рис.8.10). Линии пересече­ния двух цилиндров, двух конусов или цилиндра и конуса, описанные около сферы, будут плоски­ми кривыми - эллипсами, фронтальные проекции которых представ­ляют собой отрезки прямых (рис.8.10).

На рис.8.11 вынесенными сечения­ми показан действительный вид двух плоских кривых (эллипсов), полу­чившихся при пересечении цилиндра и конуса, описанных около одного и того же шара.

 

Рис.8.10	Рис. 8.11