
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное положение двух плоскостей, прямой и плоскости.Содержание книги
Поиск на нашем сайте
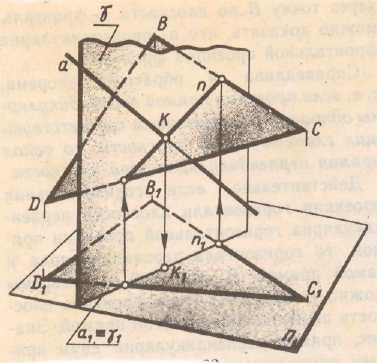
Две плоскости в пространстве могут быть параллельны или пересекаться между собой. Плоскости параллельны между собой, если в каждой из них можно построить по две пересекающиеся между собой прямые так, что две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Если плоскости параллельны и задаются следами, то их одноименные проекции следов так же параллельны. Если плоскости не параллельны в пространстве, то они пересекаются.
Рис.4.1
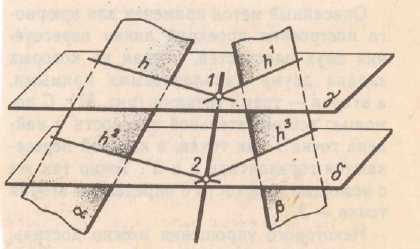
Построение линии пересечения двух плоскостей.
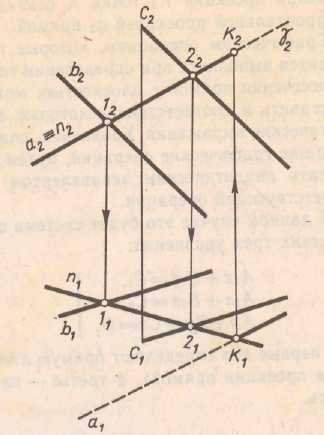
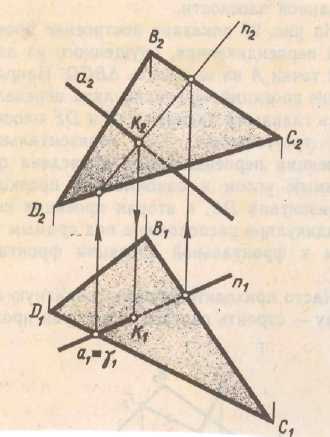
Прямая линия получаемая при взаимном пересечении двух плоскостей вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям. Для построения линии пересечения необходимо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям, эти точки и определяют линию пересечения двух плоскостей.
Рис.4.2
Рис. 4.3
Пересечение двух плоскостей, одна из которых задана следами другой любым другим способом
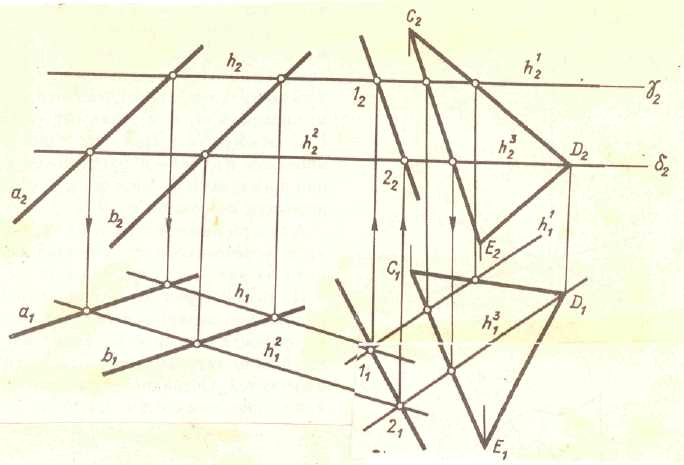
Алгоритм решения задачи на построение линии пересечения двух плоскостей: 1) вводятся вспомогательные секущие плоскости, лучше всего плоскости частного положения; (Рис.4.2) 2) строятся линии пересечения вспомогательных и заданных плоскостей; 3) определяются две точки принадлежащие линии пересечения двух плоскостей; 4) проводятся линии пересечения двух плоскостей. Взаимное положение прямой и плоскости в пространстве: 1) прямая принадлежит плоскости; 2) прямая пересекает плоскость; 3) прямая параллельна плоскости; 4) прямая перпендикулярна плоскости.
Пересечение прямой линии с плоскостью Алгоритм решения: 1) через данную прямую провести некоторую вспомогательную секущую плоскость (проецирующую); Рис.4.4 2) построить линию пересечения вспомогательной плоскости и заданной; Зафиксировать положение точки пересечения прямой с плоскостью, которая определится как точка пересечения прямых заданной и построенной линии пересечения.
Рис.4.4
ЛЕКЦИЯ № 5 Способы преобразования чертежа.
Решение задач позиционного и главным образом метрического характера значительно облегчается когда данные элементы располагаются на прямых или на плоскостях частного положения. При решении метрических задач, которые связаны с определением истинных размеров изображаемых на эпюре фигур, могут встретиться трудности, если заданные проекции не подвергнуть специальным преобразованиям. Такими преобразованиями являются: 1) способ замены плоскостей проекций; 2) способ вращения; 3) способ плоскопараллельного перемещения. В этой лекции мы рассмотрим эти способы, которые дадут возможность переходить от общих положений прямых и плоских фигур к частным в системе плоскостей П1 и П2. Способ замены плоскостей проекций заключается в том, что положение точек линий, плоских фигур поверхностей в пространстве остается неизменным, а система плоскостей проекций П1П2 дополняется новыми плоскостями проекций так, чтобы получаемые на них проекции обеспечивали рациональное решение, но каждая новая система плоскостей проекций должна быть ортогональной. В некоторых случаях для решения задачи достаточно введение одной дополнительной плоскости проекций. Обычно вводится новая плоскость проекций перпендикулярно горизонтальной плоскости проекций при этом сама плоскость проекций является горизонтально-проецирующей или вводится новая плоскость проекций перпендикулярная фронтальной плоскости проекций при этом сама плоскость проекций является фронтально-проецирующей плоскостью. Если введение одной дополнительной плоскости проекций недостаточной для решения задачи, то вводят дополнительные плоскости проекций, но уже к измененной системе плоскостей проекций. Можно представить переход от одной системы плоскостей проекций к последующим системам в следующем виде:
Рассмотрим некоторые примеры.
Определим натуральную величину отрезка прямой общего положения. Решение: нам известно, что если отрезок прямой параллелен какой-либо плоскости проекций, то на данную плоскость проекций этот отрезок проецируется в натуральную величину. Это положение позволяет нам ввести дополнительную плоскость проекций таким образом, что она будет перпендикулярна горизонтальной плоскости проекций и в тоже время параллельна самому отрезку. На новую плоскость проекций заданный отрезок спроецируется в натуральную величину. Рис.5.1 (а) При решении данной задачи можно было ввести дополнительную плоскость фронтально-проецирующую и параллельную самому отрезку и получить тот же самый конечный результат. Рис 5.1 (б)
Рис 5.1
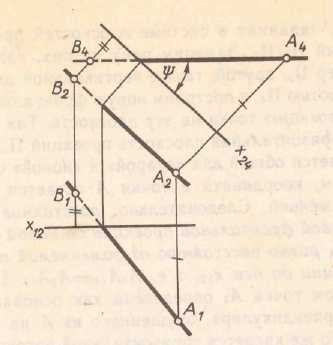
Рассмотрим еще один пример. Введение дополнительной плоскости проекций дает возможность преобразовать чертеж так, что плоскость общего положения заданная в системе
а)
б) Рис.5.2
Способ вращения
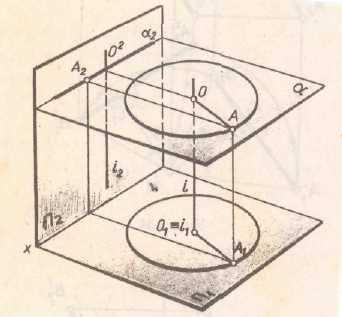
Способ вращения заключается в том, что положение данной геометрической фигуры относительно неподвижных плоскостей проекций изменяют посредством поворота ее вокруг некоторой оси. Для осуществления этого способа необходимо задать некоторую неподвижную прямую – ось вращения. Каждая точка вращаемого объекта перемещается в плоскости перпендикулярной к оси вращения. При этом любая точка объекта будет перемещаться по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра вращения (радиус вращения). Ось вращения может быть задана или выбрана. Если ось вращения перпендикулярна к плоскости П2, то плоскость в которой происходит вращение точки А параллельна плоскости П2. Следовательно траектория движения точки проецируется на П2 без искажения, а на П1 – в виде отрезка прямой. Рис 5.3
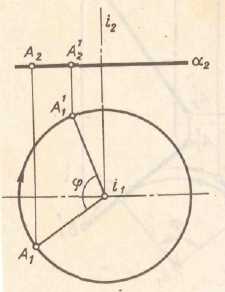
Рис 5.3 Вращение точки вокруг заданной оси перпендикулярно к плоскости проекций. Пусть точка А вращается вокруг оси перпендикулярной к плоскости П1. Через точку А проведена плоскость перпендикулярная к оси вращения и следовательно параллельна П1. При вращении точка А описывает в плоскости окружность радиуса R. Величина радиуса выражается длинной перпендикуляра проведенного из точки А на ось. Окружность описанная в пространстве точкой А проецируется на П1 без искажения, а на П2 – в виде отрезка прямой. Рис 5.4 (а) на рис 5.4 (б) на П1- в виде отрезка прямой
Рис 5.4 Требуется определить натуральную величину отрезка прямой общего положения способом вращения. При решении данной задачи ось вращения удобно выбрать проходящей через один из концов отрезка. Построение при этом упростится, так как точка через которую проходит ось будет неподвижной и для поворота отрезка надо построить новое положение проекций точки одной точки – другого конца прямой. Рис.5.5(а) Если выбрать ось перпендикулярную П1 и провести ее через точку В, то нужно поворачивать точку А до тех пор пока отрезок не займет положение параллельное фронтальной плоскости проекций. Рис 5.5 (б)
Рис 5.5
Способ вращения в дальнейшем будем использовать при построении разверток различных поверхностей. И в заключении рассмотри применение способа вращения без указания на чертеже осей вращения перпендикулярных к плоскости П1. Этот случай вращения называют способ плоскопараллельного перемещения и заключается он в том, что данный элемент в пространстве перемещается таким образом, что все точки его всё время находятся во взаимно-параллельных плоскостях. На этом эпюре перемещение осуществляют параллельно плоскостям проекций П1 или П2, когда каждая точка фигуры движется в плоскостях уровня. Рис 5.6
Рис 5.6
Этот способ имеет преимущество перед вращением. Упрощается построение, не происходит наложений одной проекции на другую.
ЛЕКЦИЯ № 6
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.009 с.) |


 а)
а)
 б)
б)
 в)
в)
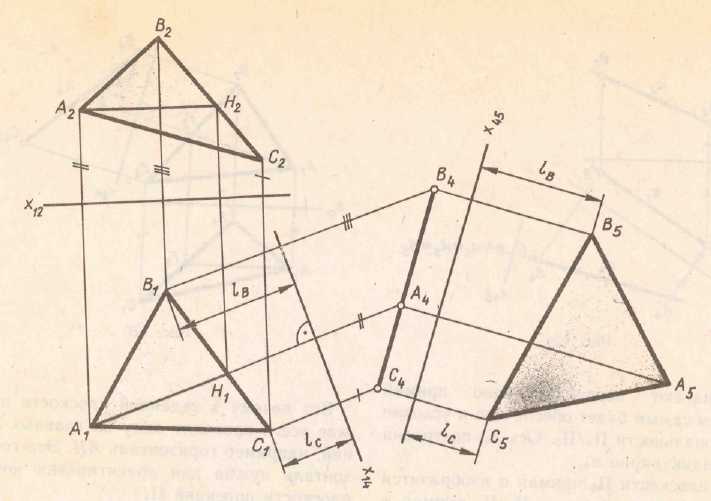
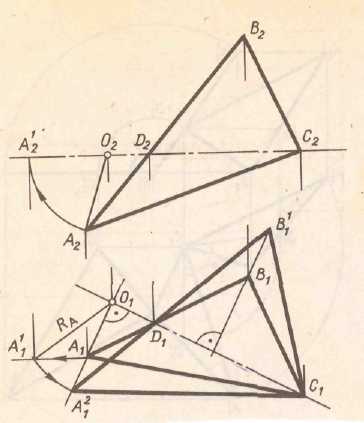
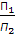 становится частного положения в новой системе плоскостей проекций. Рис.5.2(а). На рис 5.2 (б) второй определена натуральная величина треугольника АВС
становится частного положения в новой системе плоскостей проекций. Рис.5.2(а). На рис 5.2 (б) второй определена натуральная величина треугольника АВС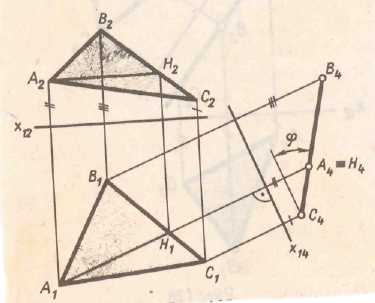
 а)
а)
 б)
б)
 а)
а)
 б)
б)




