
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции ненагруженного дискаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Измерить диаметр D нижнего диска, диаметр d верхнего диска и длину L нити. Масса диска 2. Повернуть диск на угол 5 – 6 градусов вокруг оси 3. Повторить измерения еще 2 раза и результаты записать в таблицу 5. 4. Определить среднее время 20 колебаний и рассчитать средний период колебаний T по формуле 5. По формуле (10) вычислить момент инерции ненагруженного диска. 6. Рассчитать относительную и абсолютную погрешности измерения момента инерции диска 7. Внести результаты измерений и расчетов в таблицу 5.
Таблица 5. Момент инерции ненагруженного диска
Определение момента инерции сплошного цилиндра относительно оси, проходящей через центр масс тела 1. Измерить диаметр 2. Расположить цилиндр на диске так, чтобы его ось симметрии совпала с осью 3. Повернуть диск на угол 5 – 6 градусов вокруг оси 4. Рассчитать среднее время и определить период колебаний Т нагруженного диска по формуле 5. По формуле (10) вычислить момент инерции 6. По формуле (11) определить момент инерции 7. Рассчитать погрешности измерения момента инерции сплошного цилиндра 8. Рассчитать момент инерции сплошного цилиндра относительно оси вращения, проходящей через его центр инерции, по формуле
9. Сравнить значения момента инерции сплошного цилиндра, полученные экспериментально и теоретически. 10. Внести результаты измерений и расчетов в таблицу 6.
Таблица 6. Момент инерции диска с цилиндром
Проверка теоремы Штейнера 1. Записать в таблицу массу 2. Расположить строго симметрично относительно оси 3. Измерить расстояние 4. Повернув диск с цилиндрами на 5 – 6 градусов относительно 5. По формуле (10) рассчитать момент инерции 6. Определить момент инерции
где момент инерции диска 7. Рассчитать погрешности измерения. 8. Теоретическое значение момента инерции цилиндра, расположенного на расстоянии s от оси вращения, определить по формуле
где диаметр 9. Результаты измерений внести в таблицу 7. 10. Сравнить экспериментальное значение момента инерции сплошного цилиндра, расположенного на расстоянии s от оси вращения, с теоретически рассчитанным значением.
Таблица 7. Момент инерции диска с двумя цилиндрами
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.247 (0.009 с.) |

 указана на установке.
указана на установке. и измерить секундомером время 20 полных колебаний.
и измерить секундомером время 20 полных колебаний. , где n – число колебаний.
, где n – число колебаний.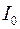 .
.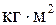
 ,
,
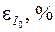
 цилиндра и взвесить его массу
цилиндра и взвесить его массу  на аналитических весах. Записать в таблицу 6 массу цилиндра и системы
на аналитических весах. Записать в таблицу 6 массу цилиндра и системы  равную сумме масс цилиндра и диска.
равную сумме масс цилиндра и диска. системы.
системы. сплошного цилиндра, используя значение
сплошного цилиндра, используя значение  .
. .
.

 ,
, 
 ,
, 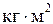
 системы равную сумме масс двух цилиндров и диска.
системы равную сумме масс двух цилиндров и диска. между центром цилиндра и осью
между центром цилиндра и осью  системы.
системы. одного цилиндра по формуле
одного цилиндра по формуле ,
, ,
, ,
, 
 ,
, 


