
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов косвенного измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В лабораторной практике большинство измерений – косвенные и интересующая величина является функцией одной или нескольких непосредственно измеряемых величин:
Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (10) средних значений непосредственно измеряемых величин, т.е.
Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных. Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам
или
где Формулой (11) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (12) применять целесообразно, если функция имеет вид произведения или частного аргументов. Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:
или
где В этом случае надежность для доверительного интервала Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:
При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений. Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий. При обработке результатов косвенных измерений предлагается следующий порядок операций: 1. Все величины, находимые прямыми измерениями, обработать в соответствии с правилами обработки результатов прямых измерений. При этом для всех измеряемых величин задать одно и то же значение надежности P. 2. Оценить точность результата косвенных измерений по формулам (11) – (12), где производные вычислить при средних значениях величин. Если ошибка отдельных измерений входит в результат дифференцирования несколько раз, то надо сгруппировать все члены, содержащие одинаковый дифференциал, и выражения в скобках, стоящие перед дифференциалом взять по модулю; знак d заменить на Δ (или δ). 3. Если случайная и систематическая ошибки по величине близки друг к другу, то их необходимо сложить по правилу сложения ошибок. Если одна из ошибок меньше другой в три или более раз, то меньшую можно отбросить. 4. Определите относительную погрешность результата серии косвенных измерений
5. Результат измерения записать в виде:
Пример. Находится объем цилиндра по формуле
где d – диаметр цилиндра, h – высота цилиндра. Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты:
при одинаковой надежности Среднее значение объема, согласно (11) равно
Воспользовавшись выражением (14) имеем:
Так как измерения производились микрометром, цена деления которого 0.01 мм, систематические ошибки
Систематическая ошибка оказывается сравнимой со случайной, следовательно
Относительная погрешность
Таким образом, результат измерения после оказывается
или окончательно после округления имеет вид
Метод наименьших квадратов Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x. В результате измерений получается ряд значений:
По данным такого эксперимента можно построить график зависимости Суть метода наименьших квадратов состоит в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут те, при которых сумма квадратов отклонений экспериментальных значений функции На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением Для начала рассмотрим зависимость
Величина
или
Вычисление показывает, что среднеквадратичная ошибка определения величины k при этом равна
Теперь можно рассмотреть более трудный случай, когда точки должны удовлетворить формуле Задача состоит в том, чтобы по имеющемуся набору значений Составляя квадратичную форму
определяют значения a и b, при которых
Совместное решение этих уравнений дает
Среднеквадратичные ошибки определения a и b равны
При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (15) – (20). Формы этих таблиц приведены в рассматриваемых ниже примерах. Пример 1. Исследовалось основное уравнение динамики вращательного движения
Таблица 2. Результаты эксперимента
Используя линейную зависимость
по формуле (15) определяем
откуда Для определения среднеквадратичной ошибки воспользуемся формулой (16)
По формуле (14) имеем
Задавшись надежностью
Относительная погрешность
Окончательно результат можно записать в виде:
Пример 2. Вычислить температурный коэффициент сопротивления металла по методу наименьших квадратов. Сопротивление зависит от температуры по линейному закону
Свободный член определяет сопротивление Результаты измерений и расчетов приведены в таблице 3.
Таблица 3. Результаты эксперимента
По формулам (17), (18) определяем
Отсюда:
Найдем ошибку в определении
Пользуясь формулами (19), (20) имеем
Тогда
Задавшись надежностью
Относительная погрешность
Окончательно результат можно записать в виде:
РАЗДЕЛ 3. Лабораторные работы Лабораторная работа № 1 Определение плотности твердых тел правильной Цели и задачи работы Цели работы: – Изучение устройства штангенциркуля и микрометра. – Измерение геометрических размеров тел с помощью измерительных приборов. – Освоение методики взвешивания на аналитических весах. Задачи работы: – Определение плотности однородного тела цилиндрической формы и формы параллелепипеда. – Определение погрешности измерений. Теоретическая часть Для более точных измерений геометрических размеров тел применяется штангенциркуль и микрометр. Штангенциркуль. Штангенциркуль служит для измерения наружных и внутренних размеров тел с точностью до Шкала нониуса строится так, чтобы N делений нониуса соответствовали
отсюда
При
и называется точностью нониуса. Точность нониуса равна отношению цены деления основной шкалы При совмещении m -го деления нониуса с
Отсюда вытекает следующее правило отсчета длины с помощью нониуса: измеряемая длина l равна числу целых делений основной шкалы до нуля нониуса
Максимальная погрешность отсчета по нониусу равна его точности. Измеряемое тело помещают между ножками Микрометр. Микрометр применяет для измерения наружных и внутренних размеров тел и измерения глубины отверстий с точностью до Винт вращается во втулке D, вдоль которой снаружи нанесена двойная шкала с делениями через 0.5 мм по обе стороны продольной черты таким образом, что верхняя сдвинута относительно нижней на половину деления. На винт насажен барабан C, края которого при вращении винта перемещается относительно шкалы, нанесенной на втулке. По краю барабана нанесена шкала, подразделяющая окружность барабана на
Для равномерного нажима микровинта на поверхность измеряемых тел микровинт снабжается фрикционной головкой Т, называемой трещоткой, вращение которой вызывает перемещение винта только до упора его в поверхность тела, после чего фрикционная головка свободно прокручивается, издавая треск. Микрометры изготавливаются с пределами измерений Прежде чем приступить к работе с микрометром, необходимо проверить его исправность – нули шкалы, нанесенной на втулке, и шкалы барабана должны совпадать. Измеряемый предмет помещается между упором A и винтом B и вращением барабана C подводят торец винта к поверхности предмета. Окончательное нажатие микровинта следует делать только рукояткой E. Момент нажатия фиксируется слабым треском. После этого треска дальнейшее вращение рукоятки E бесполезно, а барабана – недопустимо. Производят отсчет по шкале втулки
Пример отсчета по микрометру показан на рис. 5.
здесь
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.99.80 (0.012 с.) |

 .
.
 .
.
 ,
,
 ,
,
 – частные производные функции (10) по аргументу
– частные производные функции (10) по аргументу  найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;
найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;  – систематические ошибки аргументов.
– систематические ошибки аргументов. ,
,
 ,
,
 – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов
– доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов  .
.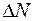 будет тоже P.
будет тоже P. .
. найти абсолютную погрешность.
найти абсолютную погрешность. .
.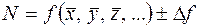 .
. ,
, ,
, ,
, .
. .
. ;
; ,
,  ;
; ;
; .
. . На основании (12) систематическая ошибка
. На основании (12) систематическая ошибка 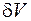 будет
будет .
. .
. .
.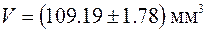
 при
при  .
. ;
; .
. . Полученная кривая дает возможность судить о виде функции
. Полученная кривая дает возможность судить о виде функции  . Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Оптимальный подход к решению подобных задач возможен на основе применения метода наименьших квадратов.
. Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Оптимальный подход к решению подобных задач возможен на основе применения метода наименьших квадратов. от значений самой функции y, т.е.
от значений самой функции y, т.е.  является наименьшей.
является наименьшей. или
или  .
. , то на графике строят зависимость n от
, то на графике строят зависимость n от  .
. – сумму квадратов отклонений экспериментальных точек от прямой
– сумму квадратов отклонений экспериментальных точек от прямой .
.
 .
.
 .
.
 найти наилучшие значения a и b.
найти наилучшие значения a и b.
 ,
, .
. ,
,
 .
.
 ,
,
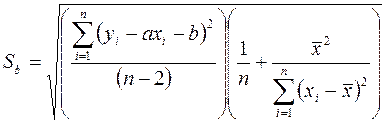 .
.
 (прямая, проходящая через начало координат). При различных значениях момента M измерялось угловое ускорение ε некоторого тела. Требуется определить момент инерции этого тела. Результаты измерений момента силы и углового ускорения занесены во второй и третий столбцы таблицы 2.
(прямая, проходящая через начало координат). При различных значениях момента M измерялось угловое ускорение ε некоторого тела. Требуется определить момент инерции этого тела. Результаты измерений момента силы и углового ускорения занесены во второй и третий столбцы таблицы 2.
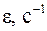







 ,
, ,
,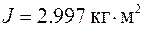 .
. .
. .
. , по таблице коэффициентов Стьюдента для
, по таблице коэффициентов Стьюдента для  , находим
, находим 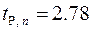 и определяем абсолютную ошибку
и определяем абсолютную ошибку .
. .
. ,
,  .
. .
.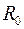 при температуре 0° C, а угловой коэффициент – произведение температурного коэффициента
при температуре 0° C, а угловой коэффициент – произведение температурного коэффициента  на сопротивление
на сопротивление 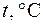








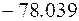



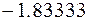



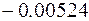

 ,
, .
. .
. , то по формуле (14) имеем:
, то по формуле (14) имеем: .
. ,
,
 .
.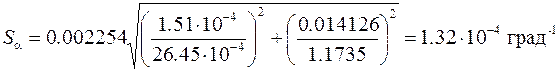 .
.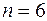 , находим
, находим  и определяем абсолютную ошибку
и определяем абсолютную ошибку .
. .
.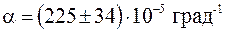 при
при  .
. . Он состоит из прочной негнущейся масштабной линейки М (рис. 2), с одной стороны которой имеется неподвижная ножка
. Он состоит из прочной негнущейся масштабной линейки М (рис. 2), с одной стороны которой имеется неподвижная ножка 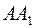 , и подвижной рамки с ножкой
, и подвижной рамки с ножкой  . В подвижной рамке укреплена вспомогательная шкала – линейный нониус D, с помощью которого производят отсчет долей деления шкалы. Винт C служит для зажима рамки, а гайка E – для плавной (микрометрической) ее подачи. Части
. В подвижной рамке укреплена вспомогательная шкала – линейный нониус D, с помощью которого производят отсчет долей деления шкалы. Винт C служит для зажима рамки, а гайка E – для плавной (микрометрической) ее подачи. Части  обеих ножек служат для измерения внутренних размеров тел.
обеих ножек служат для измерения внутренних размеров тел. делениям основной шкалы (k – целое число). Обозначим цену деления основной шкалы через
делениям основной шкалы (k – целое число). Обозначим цену деления основной шкалы через  , цену деления нониуса через
, цену деления нониуса через  . Тогда
. Тогда ,
, .
.
 разность между ценой деления основной шкалы и ценой деления нониуса равна
разность между ценой деления основной шкалы и ценой деления нониуса равна
 ,
,  . Если совместить нулевое деление шкалы такого нониуса с нулевым делением основной шкалы, то десятое деление нониуса окажется совмещенным с девятым делением основной шкалы. При этом первое деление нониуса не дойдет до первого деления основной шкалы на 0.1 мм, второе деление нониуса не дойдет до второго деления основной шкалы на 0.2 мм и т.д. (рис. 3, а). Сдвинув нониус так, чтобы его первое деление совпало с первым делением основной шкалы, мы создадим между нулевыми делениями обеих шкал расстояние 0.1 мм (рис. 3, б).
. Если совместить нулевое деление шкалы такого нониуса с нулевым делением основной шкалы, то десятое деление нониуса окажется совмещенным с девятым делением основной шкалы. При этом первое деление нониуса не дойдет до первого деления основной шкалы на 0.1 мм, второе деление нониуса не дойдет до второго деления основной шкалы на 0.2 мм и т.д. (рис. 3, а). Сдвинув нониус так, чтобы его первое деление совпало с первым делением основной шкалы, мы создадим между нулевыми делениями обеих шкал расстояние 0.1 мм (рис. 3, б). делением основной шкалы нулевое деление нониуса окажется между R и
делением основной шкалы нулевое деление нониуса окажется между R и  делениями основной шкалы. При этом сдвиг нулевого деления нониуса относительно R -го деления основной шкалы будет составлять m десятых долей миллиметра.
делениями основной шкалы. При этом сдвиг нулевого деления нониуса относительно R -го деления основной шкалы будет составлять m десятых долей миллиметра.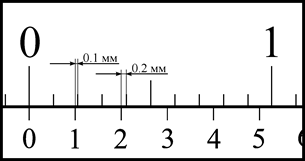

 , сложенному с точностью нониуса, умноженной на номер деления m нониуса, совпадающего с одним из делении основной шкалы
, сложенному с точностью нониуса, умноженной на номер деления m нониуса, совпадающего с одним из делении основной шкалы .
. . Микрометр для наружных измерений (рис. 4) представляет собой массивную стальную скобу, на концах которой находятся друг против друга неподвижный упор А и микрометрический винт В.
. Микрометр для наружных измерений (рис. 4) представляет собой массивную стальную скобу, на концах которой находятся друг против друга неподвижный упор А и микрометрический винт В.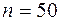 равных частей. Одному полному обороту микровинта соответствует линейное перемещение края барабана на 0.5 мм. Иначе говоря, шаг микровинта
равных частей. Одному полному обороту микровинта соответствует линейное перемещение края барабана на 0.5 мм. Иначе говоря, шаг микровинта 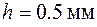 . Следовательно, точность нониуса, или цена деления нониусной шкалы, равна
. Следовательно, точность нониуса, или цена деления нониусной шкалы, равна 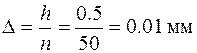 .
.
 .
. , т.е.
, т.е.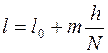 .
.
 ,
, ,
,  ,
, 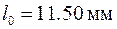 .
.


