
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка зависимости момента инерции от распределения массы тела относительно оси вращения
1. Записать в таблицу массу 2. Расположить параллелепипед основанием на диске так, чтобы ось симметрии проходила через ось 3. Повернув диск с параллелепипедом на 5 – 6 градусов относительно 4. По формуле (10) вычислить момент инерции 5. По формуле (11) определить момент инерции 6. Расположить параллелепипед другой боковой гранью на диске так, чтобы ось симметрии проходила через ось 7. Повернув диск с параллелепипедом на 5 – 6 градусов относительно 8. По формуле (10) вычислить момент инерции 9. По формуле (11) определить момент инерции 10. Результаты измерений и вычислений занести в таблицу 8. 11. Сравнить значения
Таблица 8. Момент инерции диска с параллелепипедом
2.5. Контрольные вопросы 1. Что называется моментом инерции материальной точки относительно оси вращения? Что называется моментом инерции тела относительно оси вращения? 2. В чем заключается физический смысл момента инерции? 3. В чем суть теоремы Штейнера? 4. Чему равен момент инерции стержня, ось вращения у которого проходит через конец стержня, перпендикулярно ему? 5. Как теорема Штейнера проверяется экспериментально? 6. В какие моменты времени абсолютное значение угловой скорости диска будет максимальным? 7. Какой закон сохранения применяется при выводе формулы для определения момента инерции экспериментальным путем? Сформулируйте его. 8. Выведите формулы для расчета моментов инерции полого (не тонкостенного) и сплошного цилиндров относительно оси симметрии. 9. Выведите формулу для расчета момента инерции шара.
Лабораторная работа № 3 Определение ускорения силы тяжести при
Цели и задачи работы Цель работы: – Ознакомление студентов с методом измерения ускорения свободного падения тела. Задачи работы: – Определение ускорения силы тяжести при свободном падении тела. – Изучение зависимости ускорения силы тяжести от размеров и массы тел. Теоретическая часть Ускорение силы тяжести Ускорение – векторная величина, характеризующая быстроту изменения вектора скорости тела по его численному значению и направлению. Вектор ускорения
При неравномерном движении тела по криволинейной траектории
Первое слагаемое характеризует быстроту изменения модуля скорости. Его называют тангенциальным (или касательным) ускорением, Ускорение свободного падения (или ускорение силы тяжести) – ускорение, сообщаемое свободной материальной точке силой тяжести. Такое ускорение имело бы любое тело при падении на Землю с небольшой высоты в безвоздушном пространстве. Основное уравнение динамики Ньютона
справедливо только в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальной системы с ускорением называются неинерциальными. В неинерциальных системах основной закон динамики Ньютона следует изменить, введя в рассмотрение силы особого рода – силы инерции
Силы инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления и имеют различный вид. Чтобы записать основное уравнение динамики в неинерциальной системе отсчета, рассмотрим две системы отсчета (инерциальную a) Если
Появление силы инерции при ускоренном поступательном движении испытывает каждый, кто пользуется городским транспортом. Пассажир, сидящий по ходу автомобиля, под действием силы инерции прижимается к спинке сиденья, когда автомобиль трогается с места. При торможении транспорта, сила инерции направлена в противоположную сторону, и пассажир отделяется от спинки сиденья. б) Если
Эту силу называют центробежной силой инерции, где в) На тело, движущееся поступательно со скоростью
Вектор Раскрывая содержание
При изучении движения тел относительно земной поверхности нужно иметь в виду, что система отсчета, связанная с Землей не инерциальна. Земной шар совершает сложное движение: вращается вокруг своей оси (суточное вращение) и движется по орбите вокруг Солнца (годичное вращение). Центростремительное ускорение, соответствующее движению земли по орбите (годичное вращение), гораздо меньше, чем центростремительное ускорение, связанное с суточным вращением Земли. Поэтому с достаточной точностью можно считать, что система отсчета, связанная с Землей, вращается относительно инерциальных систем с постоянной угловой скоростью суточного (
Если не учитывать вращение Земли, то тело, лежащее на ее поверхности, следует рассматривать как покоящееся, сумма действующих на это тело сил равнялось бы тогда нулю. На самом же деле любая точка А поверхности земного шара, лежащая на географической широте
где
Сила
Следует помнить, что центробежные силы, как и всякие силы инерции, существуют лишь в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам отсчета. Наблюдаемое относительно Земли ускорение свободного падения тел
есть сила тяжести.
Отличие силы тяжести
в то время как На полюсах
заменяя синус малого угла приближенно значением самого угла, получим Таким образом, в зависимости от географической широты Следовательно, во всех точках земной поверхности, за исключением полюсов, сила тяжести тела меньше силы его гравитационного притяжения к Земле. Так, на экваторе Как следует из формулы (2), если бы Земля была правильным шаром со сферически-симмтричным распределением вещества в нем, то Ускорение свободного падения Ускорение свободного падения Воспользовавшись уравнением (3) и пренебрегая влиянием суточного вращения Земли, найдем
где Из (3) следует, что: а) ускорение свободно падающего тела не зависит от массы, размеров и других характеристик тела, поэтому все тела свободно падают в безвоздушном пространстве с одинаковыми ускорениями; б) при удалении от поверхности Земли ускорение свободно падающего тела изменяется по закону
где Вблизи поверхности Земли (
т.е. с подъемом на 1 км ускорение силы тяжести уменьшается приблизительно на 0.03%. Измерить ускорение свободного падения можно при помощи: а) математического маятника; б) оборотным маятником для которого возможно измерить приведенную длину l и период T, а затем определить g из соотношения
в) наблюдением свободного падения тел, при котором путь h, пройденный телом за время t, связан с g соотношением
В данной работе использован последний метод определения Описание установки Установка для проведения опыта состоит из рейки 1 длиной 1.5 м с делениями. Вдоль рейки может перемещаться ползунок с электромагнитом 2. Электромагнит служит для удержания металлического тела. В нижней части рейки имеется платформа и рубильник 3, автоматически (при ударе шарика) выключающий секундомер 4. Устанавливая электромагнит на различную высоту вдоль рейки (рисунок 10), можно изменять высоту падения h шарика. Таким образом, определяя время падения шарика с различных высот, можно опытным путем найти ускорение свободного падения g.
Приборы и принадлежности – Экспериментальная установка – 1 шт. – Набор шаров разного диаметра – 3 шт. – Набор тел одинакового объема и разной массы – 2 шт.
Порядок выполнения работы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.119.199 (0.147 с.) |
 системы равную сумме масс параллелепипеда и диска.
системы равную сумме масс параллелепипеда и диска. .
. нагруженного диска.
нагруженного диска. системы.
системы. параллелепипеда, используя значение
параллелепипеда, используя значение 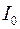 из первого задания.
из первого задания. нагруженного диска.
нагруженного диска. нагруженного диска, используя значение периода
нагруженного диска, используя значение периода  параллелепипеда, используя значение
параллелепипеда, используя значение 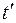 , c
, c

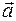 равен первой производной от вектора скорости
равен первой производной от вектора скорости  по времени:
по времени: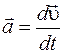 .
.
 .
.
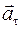 направлено по касательной к траектории. Второе слагаемое
направлено по касательной к траектории. Второе слагаемое 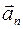 характеризует быстроту изменения направления скорости, его называют нормальным (центростремительным) ускорением,
характеризует быстроту изменения направления скорости, его называют нормальным (центростремительным) ускорением, 
 . Вместе с силами
. Вместе с силами  , обусловленными воздействиями тел друг на друга, силы инерции
, обусловленными воздействиями тел друг на друга, силы инерции 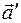 и в неинерциальных системах отсчета можно записать
и в неинерциальных системах отсчета можно записать .
.
 -систему и неинерциальную
-систему и неинерциальную 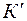 -систему):
-систему): -система движется поступательно с ускорением
-система движется поступательно с ускорением  по отношению к
по отношению к  .
.
 вокруг оси, неподвижной в
вокруг оси, неподвижной в  .
.
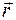 – радиус-вектор, перпендикулярный оси вращения и характеризующий положение тела относительно этой оси. Действию центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах. Эти силы используются в центробежных механизмах: насосах, сепараторах, сушилках и т.д. Центробежная сила направлена вдоль оси
– радиус-вектор, перпендикулярный оси вращения и характеризующий положение тела относительно этой оси. Действию центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах. Эти силы используются в центробежных механизмах: насосах, сепараторах, сушилках и т.д. Центробежная сила направлена вдоль оси  во вращающейся системе отсчета, кроме центробежной силы инерции действует еще одна сила инерции, называемая силой Кориолиса
во вращающейся системе отсчета, кроме центробежной силы инерции действует еще одна сила инерции, называемая силой Кориолиса .
.
 перпендикулярен векторам скорости
перпендикулярен векторам скорости 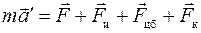 .
.
 ) вращения Земли
) вращения Земли .
.
 (рис. 9), движется около оси земного шара по кругу радиуса r с угловой скоростью
(рис. 9), движется около оси земного шара по кругу радиуса r с угловой скоростью  , т.е.
, т.е.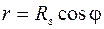 ,
,
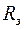 – радиус Земли, рассматриваемой в первом приближении в виде шара. Следовательно, сумма сил, действующих на такую точку, отлична от нуля и равна
– радиус Земли, рассматриваемой в первом приближении в виде шара. Следовательно, сумма сил, действующих на такую точку, отлична от нуля и равна .
.
 – это центробежная сила инерции, направленная перпендикулярно к земной оси.
– это центробежная сила инерции, направленная перпендикулярно к земной оси.
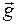 будет обусловлено действием двух сил:
будет обусловлено действием двух сил:  , с которой тело притягивается Землей (сила гравитационного притяжения Земли), и
, с которой тело притягивается Землей (сила гравитационного притяжения Земли), и 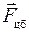 . Результирующая этих двух сил
. Результирующая этих двух сил
 .
.
 от силы притяжения к Земле
от силы притяжения к Земле  невелико, т.к. центробежная сила инерции значительно меньше, чем
невелико, т.к. центробежная сила инерции значительно меньше, чем  ,
,
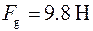 , т.е. почти в 300 раз больше, чем максимальное значение центробежной силы инерции (наблюдающееся на экваторе).
, т.е. почти в 300 раз больше, чем максимальное значение центробежной силы инерции (наблюдающееся на экваторе).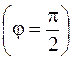
 , а на экваторе (
, а на экваторе ( )
)  . Угол
. Угол  между направлением
между направлением  ,
,
 .
. ) до 0.018 радиан или
) до 0.018 радиан или 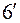 (на широте
(на широте  ).
).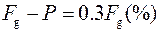 . Кроме того, везде, кроме полюсов и экватора, вектор
. Кроме того, везде, кроме полюсов и экватора, вектор  меняется с широтой в переделах от
меняется с широтой в переделах от  на экваторе до
на экваторе до  на полюсах. На широте
на полюсах. На широте  и называется «нормальным ускорением».
и называется «нормальным ускорением». ,
,
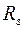 – радиус поверхности Земли, h – расстояние от центра тяжести тела до поверхности Земли.
– радиус поверхности Земли, h – расстояние от центра тяжести тела до поверхности Земли. ,
,
 – ускорения тела при его свободном падении соответственно на высоте
– ускорения тела при его свободном падении соответственно на высоте  и у поверхности Земли.
и у поверхности Земли. )
)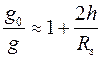 ,
,
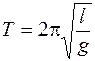 ;
;
 .
.




