
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции физического маятника в зависимости от распределения массыСодержание книги
Поиск на нашем сайте
1. Подвесить физический маятник на призму. Укрепить груз (диск) в крайнее нижнее положение. 2. Измерить время 3. Найти среднее значение времени 4. Рассчитать момент инерции
5. Переместить груз во второе положение, затем в третье, четвертое и, наконец, в самое крайнее верхнее положение и проделать аналогично пп. 2 – 4 измерения и записать результаты в таблицу 14. 6. Построить график зависимости момента инерции
Таблица 14. Момент инерции физического маятника с грузом
5.5. Контрольные вопросы 1. Что называют математическим маятником? 2. Что такое период колебания маятника? Как определить период колебаний математического маятника? 3. Почему при нахождении ускорения свободного падения измеряют время не одного, а нескольких колебаний? 4. Как выводится уравнение движения математического маятника в дифференциальной форме? 5. Как математически определяется возвращающая сила? Что означает знак «–» в уравнении движения математического маятника в дифференциальной форме? 6. Что называют физическим маятником? Как рассчитать период его колебания? 7. Что называют приведенной длиной физического маятника? Что называют центром качания? 8. Как формулируется теорема Штейнера? 9. Выведите формулы для периодов колебаний математического и физического маятников. 10. Как направлены вектора момента силы тяжести
Лабораторная работа № 6 Определение модуля Юнга по растяжению стальной проволоки Цели и задачи работы Цель работы: – Ознакомление студентов с пределами применимости закона Гука. Задачи работы: – Экспериментальная проверка закона Гука. – Определение модуля Юнга по растяжению проволоки. – Определение погрешности измерений. Теоретическая часть Закон Гука Под действием внешних сил реальные тела изменяют свои размеры и форму, т.е. происходит изменение взаимного положения частиц (молекулы, атомы) тела, связанное с их перемещением относительно друг друга. Это явление носит название деформации. Различают основные виды деформации – растяжение, сжатие, сдвиг, кручение, изгиб. В случае одноосного растяжения цилиндрического образца элементарной деформацией является удлинение. Деформации могут быть упругими и неупругими. Упругими называют деформации, при которых тело полностью восстанавливает свою первоначальную форму и размеры после прекращения действия силы. Если внешняя сила велика и перемещает частицы настолько, что их взаимодействия не могут вернуть частицы в исходные положения после прекращения действия внешней силы, то деформация называется неупругой. Деформация выражается в относительных единицах. Количественной мерой, характеризующий степень деформации, является относительная деформация. Относительным изменением длины (относительное удлинение) называется величина
где Упругую деформацию тел описывают законом Гука: если к концу стержня приложена растягивающая сила F, то его относительное удлинение пропорционально этой силе и обратно пропорционально площади поперечного сечения S
где Сила F, приходящаяся на единицу площади S сечения образца, называется нормальным напряжением
Тогда с учетом введенных обозначений закон Гука можно записать в виде
или
Из формулы (3) видно, что модуль Юнга численно равен напряжению, которое возникло бы в образце при изменении длины образца вдвое (т.е. относительном удлинении образца равном 1). Закон Гука справедлив при малых деформациях, не достигающих предела упругости, выше этого предела зависимость Из уравнения (2) следует, что при упругих деформациях абсолютное удлинение прямо пропорционально приложенной силе, т.е.
Модуль Юнга можно определить также из графика зависимости
Тогда
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.31.82 (0.01 с.) |

 N полных колебаний физического маятника. Измерения провести три раза.
N полных колебаний физического маятника. Измерения провести три раза. колебания маятника. Определить среднее значение периода колебаний маятника по формуле
колебания маятника. Определить среднее значение периода колебаний маятника по формуле  .
. физического маятника по формуле (10), где
физического маятника по формуле (10), где  – масса маятника с грузом,
– масса маятника с грузом,  – расстояние от точки подвеса до центра масс системы вычисляемая по формуле
– расстояние от точки подвеса до центра масс системы вычисляемая по формуле ,
,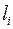 – расстояние от точки подвеса до центра масс груза. Значения l и g взять из таблицы 13 и 12 соответственно.
– расстояние от точки подвеса до центра масс груза. Значения l и g взять из таблицы 13 и 12 соответственно. и углового ускорения
и углового ускорения  при движении маятника к положению равновесия (от положения равновесия)?
при движении маятника к положению равновесия (от положения равновесия)? ,
,
 – начальная длина образца, l – длина образца после растяжения.
– начальная длина образца, l – длина образца после растяжения. ,
, – коэффициент упругости, зависящий от рода материала, E –модуль упругости или модуль Юнга.
– коэффициент упругости, зависящий от рода материала, E –модуль упругости или модуль Юнга. .
.

 .
.
 становится нелинейной. Если напряжение превосходит предел пластичности, то деформации становятся необратимыми (не исчезают после снятия напряжения). При напряжениях, превышающих предел прочности, материал разрушается.
становится нелинейной. Если напряжение превосходит предел пластичности, то деформации становятся необратимыми (не исчезают после снятия напряжения). При напряжениях, превышающих предел прочности, материал разрушается. . Зная размеры испытуемого образца, приложенную силу и относительное удлинение, можно вычислить модуль Юнга
. Зная размеры испытуемого образца, приложенную силу и относительное удлинение, можно вычислить модуль Юнга .
.
 линейно зависит от F, то тангенс угла наклона прямой
линейно зависит от F, то тангенс угла наклона прямой  .
. .
.



