
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость, коэффициент ПуассонаСодержание книги
Поиск на нашем сайте
Количество теплоты Q, необходимое для нагревания массы однородного вещества от температуры
где c – удельная теплоемкость вещества. Из формулы (1) следует
Как видно, удельной теплоемкостью вещества называется количество теплоты, необходимое для повышения температуры вещества массой 1 кг на 1 К. Теплоемкостью тела называют количество теплоты, необходимое для повышения его температуры на 1 К.
Молярной теплоемкостью называют количество теплоты, необходимое для повышения температуры 1 моля вещества на 1 К.
где
Состояние газа может быть охарактеризовано тремя величинами – давлением p, объемом V и температурой T. Уравнение, связывающее эти величины, называют уравнением состояния вещества. Для идеального газа уравнением состояния является уравнение Менделеева-Клайперона, которое имеет вид
где R – универсальная газовая постоянная. Величина теплоемкости газов зависит от условий нагревания. Для выяснения этой зависимость, необходимо воспользоваться уравнением состояния (2) и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты
Воспользовавшись определением молярной теплоемкости, получим
Из формулы (3) видно, что теплоемкость может иметь различные значения в зависимости от способа нагревания газа, так как одному и тому же значению Внутренняя энергия идеального газа – это энергия теплового движения молекул и атомов в молекулах. Она складывается из кинетических энергий поступательного и вращательного движения молекул и энергии колебаний атомов в них. Согласно закону равнораспределения энергии по степеням свободы молекулы, на каждую поступательную и вращательную степень свободы молекулы приходится в среднем энергия, равная
где i – число степеней свободы молекулы. Числом степеней свободы молекулы называют число независимых координат, определяющих положение молекулы в пространстве. Внутренняя энергия n молей газа равна
Отсюда следует, что внутренняя энергия данного количества идеального газа зависит от его абсолютной температуры, но не зависит от объема, что является следствием модели идеального газа, в которой потенциальной энергией межмолекулярного взаимодействия пренебрегают. Изменение внутренней энергии газа определяется формулой
Рассмотрим основные процессы, протекающие в идеальном газе: 1. Изохорический процесс. Процесс называется изохорическим, если объем газа при изменении температуры остается неизменным. В этом случае
2. Изобарический процесс. Процесс, протекающий при постоянном давлении, называется изобарическим. Для этого случая формула (3) перепишется в виде
Используя уравнение состояния (2) получаем:
Но
Сравнивая уравнения (4) и (5) видим, что
Уравнение (8) называется уравнением Майера. 3. Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре. В этом случае 4. Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. В этом случае
или
то есть при адиабатическом процессе расширения или сжатия, работа совершается газом только за счет изменения запаса внутренней энергии. Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии
Разделив уравнение (6) на
откуда
где Интегрируя и потенцируя последнее уравнение, получим уравнение Пуассона
Согласно кинетической теории газов из (4) и (7), получим
Эта формула справедлива как для молярных, так и для удельных теплоемкостей газов. Описание и теория метода Предлагаемый метод определения показателя адиабаты
Установка состоит из баллона 1, соединенного с манометром 2 и насосом 3 (рис. 17). Посредством крана 4 баллон может быть соединен с атмосферой, и соответственно, первоначальное давление в нем равно атмосферному. Кран 5 служит для закрытия подачи воздуха из насоса. Если с помощью насоса быстро накачать в баллон некоторое количество воздуха и закрыть кран, то давление в баллоне повысится, но если это повышение было произведено достаточно быстро, то манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, его температура повысится. Окончательная разность уровней в манометре Обозначим через
где Эти два параметра При быстром открывании крана воздух из сосуда начнет выходить в атмосферу, т.е. расширяться до тех пор, пока давление в сосуде не сравняется с атмосферным. Это расширение происходит достаточно быстро и система не успевает обменяться теплом с окружающей средой. Следовательно, воздух расширяется адиабатически, в результате чего его температура понизится до некоторого значения Если после этого снова закрыть кран, то находящийся в сосуде воздух массой
В итоге мы имеем третье состояние воздуха с параметрами Адиабатический переход воздуха из первого состояния во второе описывается законом Пуассона (9), которое, используя уравнение состояния (2), можно записать в виде
а изохорный переход из второго состояния в третье – законом Гей-Люссака
Принимая во внимание (10) и (11), из (12) и (13) получим
Логарифмируя это выражение, имеем:
В случае относительно малых изменений давления
откуда
Таким образом, при относительно небольших изменениях давления
Установка, схема которой приведена на рис. 17, связана с водяным манометром со шкалой для измерения перепада давления воздуха в баллоне по сравнению с атмосферным. Поэтому изменение давления
где h – разность высот уровней воды в манометре; r – плотность воды; g – ускорение свободного падения. Поэтому измерение
Приборы и принадлежности – Баллон – 1 шт. – Манометр – 1 шт. – Насос – 1 шт. Порядок выполнения работы 1. При закрытом кране баллона 4 открыть кран насоса 5 и с помощью насоса накачать в баллон воздух до тех пор, пока разность высот уровней воды в манометре не достигнет 10 – 15 см. Закрыть кран насоса 5. 2. Выждав 2 – 3 минуты, пока температура внутри баллона не станет равной температуре окружающего воздуха, измерить установившуюся разность высот 3. Поворотом рукоятки крана 4 открыть баллон и в момент, когда уровни воды в коленах манометра сравняются, быстро закрыть кран. 4. Выждать опять 2 – 3 минуты, пока охлажденный при адиабатическом расширении воздух нагреется до прежней (комнатной) температуры, и измерить установившуюся разность уровней 5. Поворотом крана 4 открыть баллон для установления в нем атмосферного давления. 6. Повторить опыт 15 раз, меняя каждый раз значение 7. По формуле (15) вычислить значение g, значения занести в таблицу 16. 6. Рассчитайте среднее значение g, абсолютную и относительную погрешности измерений.
Таблица 16. Коэффициент Пуассона для воздуха
7.5. Контрольные вопросы 1. Что называют удельной (молярной) теплоемкостью вещества? 2. Получите взаимосвязь между удельной и молярной теплоемкостями идеального газа, пользуясь первым началом термодинамики. 3. Что называют числом степеней свободы молекулы? Чему равно число степеней свободы для одноатомного, двухатомного, трехатомного газа? 4. Выведите формулы для определения молярных теплоемкостей при постоянном объеме и при постоянном давлении через число степеней свободы молекулы. Как записывается уравнение Майера?
5. Что такое коэффициент Пуассона? Как объяснить, что его значение для любого газа больше единицы? Чему равен коэффициент Пуассона для воздуха? 6. Какие процессы происходят с воздухом в настоящей работе? Каким законам они подчиняются? 7. Какой процесс называют адиабатическим? Получите уравнение этого процесса для идеального газа, пользуясь первым законом термодинамики и уравнением состояния. 8. Изобразите в координатах 9. Что утверждает закон равнораспределения энергии по степеням свободы молекул? Каковы границы его применимости?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.20 (0.01 с.) |

 до температуры
до температуры  , пропорционально массе вещества и изменению температуры
, пропорционально массе вещества и изменению температуры ,
,
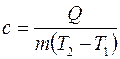 .
.
 .
.
 ,
,
 – количество молей вещества, M – молярная масса вещества. Из определения удельной теплоемкости следует, что она связана с молярной теплоемкостью соотношением
– количество молей вещества, M – молярная масса вещества. Из определения удельной теплоемкости следует, что она связана с молярной теплоемкостью соотношением .
.
 ,
,
 , переданное системе, затрачивается на увеличение ее внутренней энергии
, переданное системе, затрачивается на увеличение ее внутренней энергии  и на работу
и на работу  , совершаемую системой против внешних сил
, совершаемую системой против внешних сил .
. ,
,
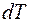 могут соответствовать различные значения
могут соответствовать различные значения 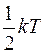 , где k – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Таким образом, средняя энергия теплового движения молекулы идеального газа равна
, где k – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Таким образом, средняя энергия теплового движения молекулы идеального газа равна ,
, .
. .
.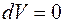 , а следовательно
, а следовательно 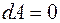 (элементарная работа газа
(элементарная работа газа  ), то есть вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (3) следует, что молярная теплоемкость газа при постоянном объеме равна
), то есть вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (3) следует, что молярная теплоемкость газа при постоянном объеме равна .
.
 .
.
 .
.
 , следовательно,
, следовательно, 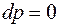 , поэтому
, поэтому  . Подставляя это выражение в уравнение (5) получим
. Подставляя это выражение в уравнение (5) получим .
.
 .
.
 и
и  , то есть внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.
, то есть внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу. . Первое начало термодинамики для такого процесса будет иметь вид:
. Первое начало термодинамики для такого процесса будет иметь вид:
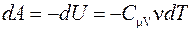 ,
, . Так как
. Так как  , то
, то .
. и учитывая последнее уравнение и (8), получим
и учитывая последнее уравнение и (8), получим ,
, ,
, – показатель адиабаты.
– показатель адиабаты. .
.
 .
. основан на применении адиабатического и изохорического процессов.
основан на применении адиабатического и изохорического процессов.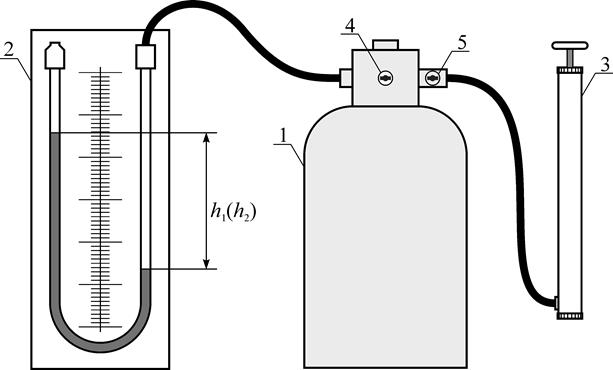
 установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.
установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха. – давление газа внутри сосуда, соответствующее показанию манометра
– давление газа внутри сосуда, соответствующее показанию манометра  ,
,

 – приращение давления, происшедшее фактически за счет увеличения массы воздуха в сосуде по сравнению с массой воздуха в начальном состоянии.
– приращение давления, происшедшее фактически за счет увеличения массы воздуха в сосуде по сравнению с массой воздуха в начальном состоянии. воздуха будет в состоянии, характеризуемом давлением
воздуха будет в состоянии, характеризуемом давлением  , температурой
, температурой  , которое назовем вторым состоянием.
, которое назовем вторым состоянием. и станет равным
и станет равным .
.
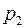 ,
,  ,
,
 .
.
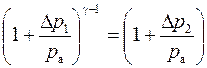 .
.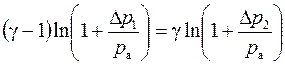 .
.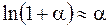 , в итоге получим
, в итоге получим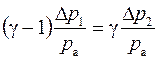 ,
,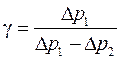 .
.
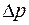 , заключенного в баллоне воздуха по сравнению с атмосферным давлением, определяется разностью высот уровней воды в коленах манометра
, заключенного в баллоне воздуха по сравнению с атмосферным давлением, определяется разностью высот уровней воды в коленах манометра ,
, высот уровней воды в коленах манометра, а формула (14) для расчета g – к формуле
высот уровней воды в коленах манометра, а формула (14) для расчета g – к формуле .
.
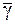


 адиабатический и изотермический процессы.
адиабатический и изотермический процессы.


