Уклон – это тангенс угла наклона или отношение превышения к горизон-

 

тальному проложению линии, выражается формулой

i = tg ν = h/a.

 

(5.1)

Уклон выражают натуральным значением тангенса, в процентах (%) или в

промилле (‰); промилле ‒ это тысячная часть целого.

 

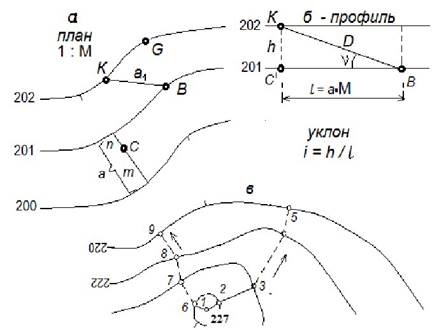
Рис. 5.4. Крутизна и направление ската, угол наклона, уклон:

а – заложение наклонной линии; б – угол наклона и уклон отрезка линии между

горизонталями; в – направления ската по линиям стока воды

 

 

Заложение, перпендикулярное к горизонталям, называется заложением ската,

то-есть, заложение ската - это горизонтальная проекция линии наибольшей кру-

тизны ската в данной точке; оно принимается за направление ската. Измерив на

карте масштаба 1: М заложение a вычисляем соответствующую ему длину линии

на местности

l = аМ,

и, зная высоту сечения рельефа h, по формуле (5.1) находим тангенс угла наклона,

а затем и сам угол наклона ν = аrс tg (h / l).

Расчет высоты сечения рельефа. При проектировании работ по созданию кар-

ты или плана высоту сечения рельефа hс выбирают в зависимости от масштаба кар-

ты, характера рельефа и назначения карты или плана. При этом условились изо-

 

 

бражать скаты крутизной свыше 45º специальным условным знаком обрыва. При-

мем, что наименьшее расстояние amin между горизонталями на карте составляет

0,25 мм. Тогда расчетную высоту сечения рельефа можно рассчитать по формуле

h с = amin M tg ν.

При 1: М = 1: 10 000; amin = 0,25 мм = 0,00025 м находим h с =0,00025×10 000 = 2,5

м.

Проведение горизонталей по отметкам точек. Чтобы провести на карте (или

горизонтали, необходимо иметь точки с известными отметками,

такие точки назовем пикетами. Пусть даны пикеты А, В, С, Е. (рис.5.5), и предпо-

лагается, что вдоль линий АВ, ВС, СЕ, ЕА, АС местность характеризуется равно-

мерным уклоном. Требуется провести горизонтали в пределах данного участка.

Процесс нахождения на линии, соединяющей два пикета, точек, через которые

пройдут горизонтали, называется интерполированием горизонталей. Известны три

способа интерполирования: аналитический, графический и на глаз. Каждый способ

основан на определении следов горизонталей между точками с подписанными от-

метками и иллюстрируется графиком в виде параллельных линий, показанным в

нижней части рисунка 5.5.

Пусть на линии АЕ плана (см. рис. 5.5) следует отметить точки 21, 22, 23, 24,

25 – следы горизонталей с названными отметками. Для этого на параллельные ли-

нии вспомогательного графика проецируются точки А и Е в точки А' и Е' со-

гласно их отметкам. Точки пересечения линии А'Е' с параллельными линиями

проецируются на линию АЕ плана как следы искомых горизонталей. Аналогично

определяются следы горизонталей на линиях АВ, ВС, СЕ, и АС плана. Затем через

них проводятся горизонтали – плавные линии. Горизонтали оформляются соответ-

ственно таблицам условных топографических знаков.

плане)

 

 

Рис. 5.5. Нанесение на план горизонталей с высотой сечения рельефа

1 м с помощью вспомогательного графика в виде параллельных линий:

 

 

Аналитический способ интерполирования горизонталей применяют при состав-

лении плана (карты) посредством компьютерных технологий. На лабораторных

занятиях будет освоен наиболее простой графический способ нахождения точек

(следов) горизонталей с использованием палетки из параллельных линий ‒ листа

 

прозрачной бумаги или пластика, на котором проведены параллельные прямые ли-

нии и подписаны их отметки как на рис. 5.5. Последний способ рассматривается

также в лекции № 19 «Тахеометрическая съемка».

 

 

ЛЕКЦИЯ № 6

 

Инженерное использование планов и карт. Решение

типовых задач по топографическим планам и картам

 

Координатная сетка

 

Одним из элементов топографической карты является сетка координатных ли-

ний. Существуют два вида координатной сетки: картографическая, образуемая ли-

ниями меридианов и параллелей, и сетка прямоугольных координат, образуемая

линиями, параллельными осям координат OX и OY.

На топографических картах меридианы и параллели являются границами листа

карты; в углах карты подписываются их долгота и широта. Внутри листа вычерчи-

вается сетка прямоугольных координат в виде квадратов, называемая иногда кило-

метровой сеткой, так как на картах масштаба 1:10 000 и мельче линии сетки прово-

дятся через целое число километров.

Вертикальные линии сетки параллельны осевому меридиану зоны (оси OX) и

имеют уравнение Y = Const; значение координаты Y подписывается у каждой ли-

нии. значение координаты X подписывается у каждой линии.

Для удобства пользования листами карт, на которых изображены граничные

участки зоны, на них показывается сетка прямоугольных координат соседней зоны.

Ширина граничной полосы с сеткой соседней зоны составляет 2o по долготе с обо-

их сторон зоны. Выходы линий координатной сетки соседней зоны наносятся на

внешнюю сторону рамки листа карты.

 

 

6.1. Перечень задач, решаемых с помощью карт и планов

Топографические планы и карты содержат различную информацию об объектах

местности и ее рельефе; эта информация позволяет решать многие геодезические

задачи; перечислим некоторые из них:

· определение прямоугольных координат X и Y точки,

· определение геодезических координат В и L точки,

· определение отметки H точки

· нанесение точки на план или карту по ее прямоугольным (X и Y) и геодезиче-

ским

(В и L) координатам,

 

 

· определение длины горизонтальной проекции линии c помощью линейного и

попе-

речного масштабов,

· определение дирекционного угла или географического азимута лини

· измерение горизонтального угла между двумя линиями

· построение профиля местности по заданной линии

· построение на плане или карте границ зон невидимости с данной точки мест-

ности

· построение на плане или карте границ зон невидимости с данной точки мест-

ности

· измерение площади участка,

· определение границ водосбора реки и ее притоков,

· проектирование береговой линии будущего водохранилища,

· определение площади зеркала и объема водохранилища,

· определение объемов земляных работ при строительстве различных инже-

нерных сооружении

· проведение на плане или карте линии с уклоном, не превышающим заданное

значение

6.2. Примеры решения задач по карте и плану

Определение геодезических координат. Схематический фрагмент топографи-

ческой карты показан на рис. 6.1, а. На западной и южной сторонах данного фраг-

мента рамки внутренние линии соответствуют изображениям меридиана с долго-

той В = 24° 00' и параллели с широтой L = 55° 20'. Изображения меридиана и па-

раллели

разделены через

1' линиями чередующейся толщины. На рис.2.6, а

подписаны значения широты южной стороны рамки В = 55° 20' и минутного деле-

ния меридиана В = 55° 21'. Чтобы определить широту точки К, с помощью циркуля

или линейки-угольника следует найти ее проекцию К ' на шкалу минут меридиана.

Приближенное значение широты точки К ' находим на глаз: ВК ≈ 55° 20,7 ≈ 55° 20'

42". Аналогично отмечаем проекцию К" точки К на шкале долгот, находим при-

ближенное значение долготы LК ≈ 24° 01,6'.

Определение прямоугольных координат точек. Горизонтальные линии ки-

лометровой сетки на схеме топографической карты (см. рис. 6.1, а) подписаны на

западной стороне рамке значениями абсцисс х = 6115 км и х = 16 км (на карте со-

 

 

кращена полная запись х = 6116), отсчитанными от экватора.

 

 

Абсцисса точки

Р равна хР = х + ∆х, где ∆х = n·М – отрезок, измеренный по плану с помощью цир-

куля-измерителя и масштабной линейки; n – длина отрезка на плане; 1: М – мас-

штаб плана.

Преобразованная (условная) ордината (см. лекцию № 3) точки Р равна уР

= у + ∆у, где у = 5312 км – преобразованная ордината вертикальной линии кило-

метровой сетки (здесь 5 – номер координатной зоны); ∆у = l·М – отрезок, измерен-

ный по плану. Действительная зональная ордината уРД получается после вычитания

500 км из значения уР (например, если уР = 5312,144 км, то уРД = 5312,144 – 500 = –

187,856 км; знак “минус” указывает, что точка Р расположена к западу от осевого

меридиана зоны № 5. Измеренные по карте значения хР и уР содержат погрешно-

сти, которые можно оценить с учетом формул (4.4) и (4.5) – см. лекцию № 4.

Определение углов ориентирования выполняют либо при помощи транспор-

тира, либо решением обратной геодезической задачи. С помощью транспортира

геодезический азимут А прямого отрезка Z 1 Z 2 можно измерить, продолжив отрезок

до пересечения с изображением меридиана в точке М. Дирекционные углы α1, α2

прямых линий Z 1 Z 2 и Z 2 Z 3 измеряют относительно северного направления верти-

кальных линий километровой сетки. Расхождение между значениями А и α равно

углу γ сближения осевого меридиана (параллельной ему линии) и геодезического

меридиана точки N (см, рис. 2.6, а). Погрешность измерения углов транспортиром

составляет 0,1–0,25°.

С точностью 1-3' дирекционный угол линий Z 1 Z 2 и Z 2 Z 3 определяется решением

обратной геодезической задачи (см. лекцию № 3). Для этого необходимо по карте

определить абсциссы и ординаты точек Z 1, Z 2 и Z 3 с помощью циркуля-измерителя

и масштабной линейки.

 

 

Рис. 6.1. Схема части топографической карты:

а – часть рамки километровой сетки; б – вертикальные линии километровой сетки (х)

и географический (Г.м) и магнитный (М.м) меридианы: в – численный и линейный

масштабы

 

Определение высоты сечения рельефа и высоты точек. Высота сечения

рельефа h с определяется, например, по подписям высоты горизонталей (см. рис.6.1,

а): между горизонталями 110 и 120 м расположены четыре ступени сечения, сле-

довательно h с = (120 – 110)/4 = 2,5 м.

Высотная координата (отметка) точки, лежащей на горизонтали, равна вы-

соте этой горизонтали (на рис. 6.1, а отметка точки G равна НG = 120 м; точки

R равна НR = 117,5 м). Отметка точки Q, лежащей между горизонталями 117,5 и

120 м равна НQ = 117,5 + ∆h, где ∆h = h с(b/a) – это часть полного сечения h с = 2,5 м,

здесь b и a – отрезки, измеряемые по плану с точностью до 0,1 мм в направлении

 

 

кратчайшего расстояния между горизонталями. Если b/a = 0,6, то ∆h = 1,5 м и НQ

= 117,5 + 1,5 = 119 м.

Погрешности отметок точек G и Q зависят от точности нанесения горизонта-

лей на план. При этом погрешность положения горизонталей зависит от угла на-

клона земной поверхности. Соответственно при углах наклона ν ≤ 2º и при углах

наклона ν > 2º максимальную погрешность 2m Н определения отметок Н относи-

тельно горизонталей оценивают величинами

2m Н ≈ h с / 4

2m' Н ≈ h с / 3,

(6.1)

 

где h с – высота сечения рельефа.

Среднее значение погрешности mН отметки Н, определенной относительно го-

ризонталей плана, оценивается соответственно углам наклона местности величи-

нами

mН ≈ h с / 8

m'Н ≈ h с / 6.

(6.2)

 

В нашем примере для результата НQ = 119 м при ν ≤ 2º оцениваем максималь-

ную погрешность 2m Н ≈ 2,5/4 = ±0,6 м и среднюю квадратическую mН ≈ 2,5/8 =

±0,3 м.

Определение крутизны ската. Задачи, решаемые с определением по карте

крутизны ската, здесь рассматриваются в развитие лекции № 6. Крутизна ската

определяется на карте по кратчайшему расстоянию а = WW 1 между двумя соседни-

ми горизонталями (см. рис. 6.1, а), которое называется заложением ската. Кру-

тизна ската рассматривается в вертикальной плоскости (рис. 6.2) и характеризуется

углом наклона ν, т.е. углом между линией ската и горизонтальной плоскостью. В

направлении заложения ската а = WW 1 (см. рис. 6.1, а) крутизна линии максималь-

на. При определении по карте угла наклона отрезка линии, произвольно ориенти-

рованного относительно горизонталей, используют заложение между соседними

горизонталями по этому произвольному направлению, например, заложение а 1 по

направлению WV на рис. 6.1, а.

Отрезков прямых линий характеризуют также уклоном. В общем случае уклон

– это отношение превышения к горизонтальному проложению между двумя точ-

ками или тангенс угла наклона т.е. согласно рис. 6.2

 

 

i = h/d = tg ν.

 

(6.3)

и

и

 

 

Уклон ската между двумя горизонталями (см. рис. 2.10) равен

i = hc /a = tg ν,

(6.4)

где hc – высота сечения рельефа; а = а п М – горизонтальное расстояние, соответст-

вующее заложению а п, измеренному на карте; М – знаменатель масштаба карты; ν

– угол наклона линии ската ТВ.

На рис. 6.2 для линии ТВ при hc = +2,5 м; а = а п М = 153 м, уклон (тангенс уг-

ла наклона) i = +0,0163.

Уклон выражают в натуральных значениях отношения h/d, в процентах (100 i),

или в промилле (1000 i). В нашем примере уклон i = +1,63%, или i = +16,3‰. Угол

наклона в градусной мере вычисляют через arc tg i, например arc tg 0,0163 =

+0,9349° = +(0° + 0,9349×60') = +0° 56'.

 

Рис. 6.2. Элементы ската

 

 

На рис. 6.1, а

 

 

заложение

 

 

ската

 

 

WW 1 = а п М = 77 м,

 

 

уклон ската i = –

2,5 / 77 = –0,0325, угол наклона ската arc tg 0,0325 = –1,859° = – (1° + 0,859×60') = –

1° 52'. В более пологом направлении WV заложение а 1 = а п М = 121 м, уклон от-

резка i = – 0,0207; угол наклона ν = –1,184° = – 1° 11'.

Графики заложений. Графики заложений используют для приближенного оп-

ределения углов наклона или уклонов по карте с горизонталями. На горизонталь-

ной оси графика углов наклона (рис. 6.3, а) через равные отрезки подписывают уг-

лы наклона в градусах. Вычисляют заложение а п по формуле

 

 

а п = (hc / tg ν): М.

 

(6.5)

 

Рис. 6.3. Графики заложений:

а – для углов наклона; б – для уклонов

 

Через концы построенных отрезков а

 

проводят плавную кривую. В раствор

циркуля-измерителя берут на карте заложение а 1, переносят его на график заложе-

ний (см. рис. 6.3, а) и определяют по графику угол наклона ν 1 = 1,6°.

ложения а 2 находим ν 2 = 4,4°.

График заложений для уклонов рассчитывают по формуле (6.6)

а п = (hc / i): М.

(6.6)

Горизонтальную ось i графика (рис. 6.3, б) размечают через выбранные интер-

валы уклонов. Плавную кривую заложений проводят через концы отрезков а п. За-

ложение, например а 3, берут с карты раствором циркуля-измерителя и по графику

определяется уклон местности i3 = 0,0073. Погрешность результатов определения

угла наклона и уклона определяется в первую очередь неточностями положения

горизонталей на плане и составляет доли градуса.