
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для управления ориентацией космического аппаратаСодержание книги
Поиск на нашем сайте Движение космического аппарата (КА) вокруг цента масс, как твердого тела произвольной конфигурации с тремя вращательными степенями свободы, описывается уравнениями вида:
где L (t)= l 0(t)+ l 1(t)+ l 2(t)+ l 3(t) – кватернион поворота КА; w (t) =w 1(t) i 1 +w 2(t) i 2 +w 3(t) i 3 – фазовые координаты (вектор угловой скорости) КА; M (t) = [ M 1(t), M 2(t), M 3(t)]T – вектор управления (вектор внешнего момента, действующего на КА). Фазовые координаты и управление подчинены требованиям задачи Л. С. Понтрягина типа L (t), w (t); || L||=l 02(t)+ l 12(t)+ l 22(t)+ l 32(t)=1; i 1, i 2, i 3 – орты гиперкомплексного пространства (мнимые единицы Гамильтона). В динамических уравнениях Эйлера (5.18.1) и (5.18.2) для КА l 1(t), l 2(t), l 3(t) – главные центральные моменты инерции КА. На модуль вектора управления наложено ограничение
Задав произвольные граничные условия по угловому положению
и угловой скорости КА
требуется определить оптимальное управление
где α 1≈ α 2= const >0, время T не задано. Записав уравнения Эйлера (5.18.2,а, 5.18.2,б и 5.18.2,в) в виде
где R 0 и R 1(w) – матрицы размерности 3×3 вида
выполняется процедура принципа максимума Понтрягина, для чего вводятся вспомогательные функции Q (t) и p (t) (кватернион и вектор, соответственно), соответствующие фазовым координатам L (t) и w (t). При этом функция Гамильтона-Понтрягина принимает вид
где q *≥0= сonst так как при q *=0 функция Гамильтона-Понтрягина соответствует задаче оценки быстродействия и не учитывает критерий (5.18.6). При q *=1 сопряженная система представима выражением
здесь символ «¤» - символ кватерионного умножения, vect (●) – векторная часть кватерниона, а R (w) – матрица размерности 3×3. Введя обозначение
где c v – произвольная векторная постоянная. Для задачи оптимального разворота сферически симметричного КА, положив I 1= I 2= I 3=1, c критерием (5.18.6) функция Гамильтона-Понтрягина (59.10) имеет вид
а краевая задача принципа максимума представима выражениями вида
Записав (5.18.16) в дифференциальном виде
(здесь символ «×» – векторное произведение), и приняв w || p, из (5.18.20) p = p 0= p (0)= const, φ определяется из
Функция Гамильтона-Понтрягина на участке t
По приведенному выше алгоритму управления требуется выполнение условий φ 0↑↑ p e и | φ 0|≥ α 2, в противном случае, с ростом t увеличивается | φ (t)|, следовательно, алгоритм управления не имеет участка свободного движения. Если же | φ 0< α 2, то алгоритм управления на первом участке носит пассивный характер, т. е. M опт=0, тогда, используя (5.18.21)
так как φ/ | φ |= p e, | p 0|=| c v|. Но траектория движения КА, при t = T,
откуда
Таким образом функция Гамильтона-Понтрягина на участке t
тогда
Откуда
а, с учетом (5.18.25)
и, подставляя значения τ 1 и τ 2 из (59.28),
С учетом (5.18.24) и (5.18.30), | c v|, | φ 0|, τ 1 и τ 2 описываются в виде
а, подставляя τ 1 и τ 2 в (5.18.23) и решая это уравнение относительно T,
Теперь задача управления ориентацией КА решена полностью. Что демонстрируется рис. 5.18.1.
Рис. 5.18.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 |≤ M max.
|≤ M max.
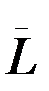 (0)=
(0)= 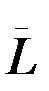 0,
0,  (T)=
(T)=  (0)=
(0)=  0,
0, 
 (α 1+ α 2|
(α 1+ α 2|  ;
;
 ;¤
;¤
 ,
,
 [0, τ 1] принимает вид
[0, τ 1] принимает вид



