
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация средств контроля и управленияСодержание книги
Поиск на нашем сайте Решение задач оптимального управления осуществляется с применением методов теории оптимальных систем управления, адаптивных управляющих систем, систем экстремального регулирования, называемых также системами автоматической оптимизации (САО). Особенность объектов управления состоит в том, что их математическая модель может быть представлена в виде последовательного соединения статистической экстремальной зависимости с априори неизвестным её видом и инерционной части, описываемой обыкновенными дифференциальными уравнениями с неизвестными стационарными коэффициентами. Разработка моделей САО и методов их проектирования затруднена отсутствием адекватных аналитических методов оценки эффективности подобных систем. Тогда появляется необходимость в САО в условиях нечеткого описания параметров, представляющая собой расширение известной задачи оптимального, с точки зрения быстродействия и точности процессов синтеза алгоритма управления, поиска многопараметрического экстремума в САО. При решении этой задачи следует выбрать такую структуру и параметры алгоритмов САО, чтобы обеспечить наилучшее качество многопараметрических процессов в различных режимах функционирования, отличающихся различными требованиями к точности и скорости отслеживания экстремума. Задача синтеза решается в условиях неполноты данных, при нечетком задании априорных параметров системы. Применение методов такой парадигмы систем автоматического управления, как системы автоматического целеуказания, теории адаптивных систем позволяет обеспечить решение задачи построения эффективного алгоритма САО для различных режимов функционирования объектов управления. Использование методов теории вероятностей и математической статистики предполагает статистически заданные возмущения, что требует проведения большого числа испытаний и обработки статистических данных. Трудности решения задач анализа и синтеза возрастают с ростом сложности (большого числа параметров и связей между элементами) систем, поэтому подобные методы разработаны для ограниченного класса САО и определенных видов случайных возмущений. Известные математические методы исследования САО при случайных возмущениях основаны, как правило, на результатах теории марковских процессов и позволяют выявить относительно полную картину процессов, но требуют аналитически сложного определения вероятностей состояний. Достаточно полное описание процессов в САО позволяет получать метод статистического имитационного моделирования. Статистическое имитационное моделирование позволяет не только исследовать переходные процессы в САО, как в динамической импульсной системе, но и получать интегральные характеристики качества функционирования системы на основе анализа реализаций процессов. Применение имитационного моделирования позволяет использовать различные математические схемы для описания объектов оптимизации, возмущений и т. п., что делает этот способ исследования практически полезным при анализе и синтезе САО реальных технических объектов. Исследования в практическом приложении направлены на разработку методов моделирования САО в условиях неполноты данных, при нечетком задании параметров, разработку проблемно-ориентированного информационного обеспечения для задач синтеза САО. Предложено применение комбинированных алгоритмов фильтрации в САО, отличающихся возможностью выделения и оценки статистических характеристик случайных возмущений, возможностью работы в условиях неопределенности уровня полезного сигнала и адаптации к неизвестным или неточно определенным характеристикам случайных возмущений. Предложен метод выбора оптимальных параметров комбинированного фильтра на основе функции риска последовательного критерия. Исследованы функции чувствительности последовательных критериев принятия решений. Приведены зависимости для определения характеристик последовательных алгоритмов. Разработан проблемно-ориентированный программный комплекс для целей имитационного моделирования и синтеза САО технических объектов. Определение системы автоматической оптимизации. В настоящее время системы автоматического управления широко применяются в различных сферах человеческой деятельности и поэтому теория автоматического управления – предмет научных исследований и основа инженерной деятельности. В любой системе автоматического управления имеется два основный блока регулятор и объект управления, как показано на рис. 4.4.1. Система управления (регулятор) предназначена для обеспечения желаемого функционирования ОУ, причем в системе управления могут быть использованы различные модели и алгоритмы управления, в зависимости от объема и качества информации об ОУ и окружающей его среде, и от цели управления.
x – вектор задающих воздействий; j – вектор возмущающих воздействий; u – вектор управляющих воздействий; y – вектор управляемых величин Рис. 4.4.1 При известной модели ОУ и заданной цели управления в виде задающего воздействия x, подаваемого на регулятор, могут быть для синтеза регулятора применены классические методы теории автоматического регулирования. Известна классификация, согласно которой, в зависимости от характера задающего воздействия x системы автоматического управления делятся на три вида систем: стабилизации, программного управления и следящие. В системах автоматического управления сложными технологическими процессами, производственными объектами существует задача оптимизации рабочего режима или хода технологического процесса согласно критериям производительности или потерь на производство единицы продукции. Эта задача решается в автоматическом режиме системами, называемыми системами экстремального управления. Управление должно быть выбрано таким, чтобы один или несколько критериев качества принимали экстремальное (минимальное или максимальное) значение. Таким образом, в системе экстремального управления цель формулируется как достижение экстремального значения: - некоторой скалярной функции параметров ОУ при заданном критерии качества; - некоторой векторной функции параметров ОУ при нескольких заданных критериях качества. Функцию или критерий оптимальности называют показателем качества или показателем экстремума ОУ. Выбор такого показателя определяется свойствами объекта управления, целью управления и ограничениями (технологическими, экономическими и пр.). Система экстремального регулирования выполняет поиск таких значений регулирующих воздействий x, которые обеспечивают оптимальные значения критерия качества при изменении внешних возмущений j, влияющих на показатель экстремума. Существуют два подхода к экстремальному регулированию: - применение способа управления по возмущению: задача экстремального управления решается непрерывным измерением внешних возмущений; - применение экстремального регулятора или системы автоматической оптимизации (САО): если измерить внешние возмущения невозможно, или неизвестен характер их влияния на изменение положения экстремума, то задача экстремального управления решается с использованием обратной связи по показателю качества работы системы. Отметим, что экстремальный регулятор применяется, как самостоятельное устройство, или как дополнение к существующей системе автоматического управления объектом для изменения уставок системы регулирования с целью поддержания заданного оптимального режима работы объекта. Для экстремальных систем управления характерно наличие поисковых движений (колебаний), при определении положении рабочей точки относительно экстремума и выборе регулирующих воздействий. Система управления может быть представлена, как некоторый автомат. На рис. 4.4.2 приведена в общем виде структура системы управления. На основе выполненного содержательного описания с учетом требований теории систем определим объект оптимизации в виде набора: < A, S A, R, S R, X, L, J, Z, Y, P, F, Q, t >, (4.4.1) где A= { ai } – множество элементов ОУ; S A – множество свойств элементов; R= { r j} – множество связей между элементами ОУ; SR – множество свойств связей между элементами; X – множество допустимых управлений; L ‑ множество входных воздействий; J – множество возмущающих сигналов; Z – допустимое множество состояний ОУ; Y – множество выходных переменных ОУ; P и F – операторы функции переходов и функции выходов, определяющие процесс функционирования ОУ; Q – показатель (критерий) качества; t – время.
z t – состояние ОУ, xt – входное управляющее воздействие, lt – входное воздействие определяющее ситуацию функционирования ОУ, jt – неконтролируемое возмущающее воздействие, yt – выход ОУ. Рис. 4.4.2 Функции переходов и функции выходов в теоретико-множественном представлении представляют собой соответствия: - функция переходов: р =< Х´L´Z,Z,Р >, так что где Р – график соответствия р; - функция выходов f =< Х´L´Z, Y, F >, так что где F – график соответствия f. В определении (4.4.1) множество элементов A, множество свойств элементов SA, множество связей между элементами R и множество свойств связей элементов SR определяют структуру ОУ. Состояние ОУ для момента t определено, как n -мерный вектор Входные воздействия ОУ делят на управляющие и направляющие воздействия. Управляющее воздействие – m -мерный вектор Возмущающее воздействие определено вектором Цели управления задаются в виде функции цели (целевой функции), которая может быть скалярной или векторной и определена, как через параметры состояния, так и через выходные переменными ОУ. Например, показатель качества можно определить следующим образом. Пусть Функция переходов (4.4.2) и функция выходов определяют процесс функционирования дискретного ОУ в общем случае равенством zt+1 = F (zt, lt, xt, jt), yt+1=Q (zt+1, lt+1, xt+1, jt+1) (4.4.4) где zt =< zt, zt-1,…, z1 >, xt =< xt, xt-1,…, x0 >, lt =< lt, lt-1,…, l0 >, jt =< jt, jt-1,…, j0 >, zt Î Z, xt Î X, lt Î L, jt Î J. Выбор параметров управления xt осуществляет САО, а значений параметров lt осуществляет система управления верхнего уровня независимо от САО. Если на множестве выходных параметров ОУ выделяют один основной параметр, характеризующий показатель качества, который может быть функцией параметров ОУ: y textr =Q t(z t ,,l t, x t, j t) (Q t – скалярная функция, имеющая экстремум), то можем говорить о робастном управлении. Отметим, что во множество X входят те воздействия на ОУ, которые обеспечивают достижение экстремального значения критерия y extr, а все другие воздействия относят к параметрам L. Теория и практика поисковых САО является одним из специфических разделов современной теории автоматического управления. Функционирование САО определяется алгоритмами импульсных помехозащищенных быстродействующих систем управления инерционными ОУ. Модель ОУ представлена последовательным соединением статической экстремальной зависимости и инерционной части, описываемой обыкновенным линейным дифференциальным уравнением. Сложность применения алгоритмов в реальном времени состоит в обеспечении устойчивости вычислений системы линейных алгебраических уравнений при идентификации показателей конечной суммы экспонент при использовании метода Прони. Рассмотрим реализацию наиболее известных алгоритмов. Однако, известные алгоритмы САО с пробными шагами применимы при малой инерционности ОУ, так как необходимо получать реакции ОУ на возмущающие пробные воздействия. Для инерционных объектов могут быть применены методы компенсации инерционности. Алгоритмы САО с совмещением пробных и рабочих операций. Подобные шаговые САО отличаются определением экстремума, применением методов повышения помехоустойчивости и уменьшения влияния инерционности ОУ за счет совмещения пробных и рабочих операций таким образом, что управляющее воздействие un на рабочем шаге одновременно является источником информации о текущем значении градиента характеристики. Принятие решения происходит по данным анализа измерений D y n1,D y n2, …, D y nk после совершения n -го рабочего шага. Казакевич В.В. разработал методы с применением модели ОУ и предварительном вычислении статической экстремальной характеристики путем идентификации переходных процессов в ОУ по методу наименьших квадратов, позволяющие синтезировать САО для ОУ, обладающих значительной инерционностью. Алгоритмы систем с синхронным детектированием. В САО с синхронным детектированием изменение пробных воздействий m n и рабочих воздействий un происходит одновременно. На вход ОУ подается регулирующее воздействие x n =m n +u n =m n +F [D y n-1(- 1)n], (4.4.5) где u n – составляющая, обусловленная детектированием сигнала модуляции, m n – постоянное модулирующее воздействие m n =a (- 1)n. (4.4.6) Для САО с синхронным детектированием предложены методы улучшения помехоустойчивости и качества процессов в САО инерционных объектов. Недостаток применения модулирующего воздействия состоит в том, что такие системы оказывают на объект управления нежелательное возмущающее воздействие большее, чем САО других типов. Алгоритмы систем с моделью экстремальной характеристики. Данный вид САО относится к беспоисковым системам оптимизации, так как модель экстремальной характеристики связывает вектор состояний ОУ с такими значениями управляющих параметров, которые позволяют вывести ОУ из текущего состояния в окрестность экстремального значения характеристики. На практике применяют САО системы заданием соответствия значений входных воздействий оптимальным значениям управляющих параметров в виде таблиц. Эти таблицы называют режимными оптимальными картами технологического процесса. Недостаток состоит в том, что число учитываемых параметров состояния ОУ ограничено ввиду роста размерности задачи, что ограничивает точность САО с данным алгоритмом функционирования. Также алгоритмы не учитывают возмущений, влияющих на технологический процесс, и требуют выполнения большого числа экспериментов для формирования режимных оптимальных карт. Задачи оптимизации в условиях неопределенности. При решении задач управления сложными технологическими процессами с применением САО определяется критериальная функция, как некоторый технико-экономический показатель. Например, при построении комплексной системы оптимизации работы энергоблока тепловой электростанции критериальной функцией может быть себестоимость произведенной электроэнергии. Однако технологический процесс реализуется на нескольких производственных участках. Следовательно, сложный процесс производства энергии должен быть условно разбит на ряд участков, для каждого из которых будет существовать собственный критерий оптимальности (коэффициент полезного действия парогенератора, тепловой эффект химической реакции, выход полезного продукта за некоторый промежуток времени и прочее), достижение которого будет способствовать достижению оптимальности всего процесса в целом. Подобная декомпозиция цели упрощает поиск оптимального управления для технологических процессов, но не является достаточным условием для поиска экстремума целевой функции, так как она является многомерной, а при решении задач управления участвуют неопределенности, которые отражают неточность (параметрическую и структурную) модели ОУ, неучитываемые возмущения входных сигналов, а также вызваны существенной инерционностью ОУ. Эти факторы могут существенно снизить эффективность систем экстремального регулирования. Возмущения в САО делят на низкочастотные и высокочастотные. Низкочастотные возмущения связаны с изменениями режима функционирования ОУ или изменением параметров состояния под действием внешних возмущений. Низкочастотные возмущения вызываю дрейф экстремальной характеристики или изменение ее вида. Высокочастотные возмущения – различные шумы и погрешности измерений, а для устранения их влияния применяют алгоритмы статистической фильтрации. Задачи компенсации возмущений остаются актуальными до настоящего времени. Так, например, методы компенсации дрейфа характеристики для каждого вида алгоритмов экстремального управления решаются по-разному. Допущения к виду модели дрейфа характеристики (монотонности, линейности на интервале измерения и прочее) снижают эффективность практического применения алгоритмов. Эффективность существующих алгоритмов автоматической оптимизации можно увеличить, если учитывать дополнительную информацию, в виде косвенной оценки возмущений. Считаются эффективными для применения в САО адаптивные и робастные методы оценки и фильтрации, ориентированные на существенную априорную неопределенность, так как обычные методы оптимальной статистической фильтрации, применяемые в САО, чувствительны к изменению статистических свойств измерений и отклонению реальных характеристик процессов от заданных, а также не учитывают нестационарность характеристик случайных процессов. Хотя известны эффективные алгоритмы статистической фильтрации на основе методов последовательной проверки статистических гипотез, обладающие адаптивными и робастными свойствами, но задача задания параметров подобных алгоритмов в условиях априорной неопределенности требует дополнительного исследования. При разработке САО инерционного ОУ надо решать задачи нахождения алгоритмов оценки состояния ОУ, обладающих необходимым быстродействием, причем решение задачи компенсации инерционности требует совместного решения задач идентификации, фильтрации, оптимального управления. Одним из приложений САО является управление энергетическими объектами, которое требует комплексного решения задач при разработке моделей и алгоритмов поиска экстремума. Отсутствие адаптивных свойств у применяемых в настоящее время алгоритмов оценки состояния ОУ снижает быстродействие САО при обеспечении устойчивой работы. Если повышать быстродействие, то САО будет более подверженной влиянию внешних возмущений. Для подавляющего большинства применяемых САО при решении задачи оптимизации производственных процессов характерен режим поиска экстремума, но не отслеживается положение экстремума в пространстве параметров, в котором САО может обеспечить соответствующее быстродействие и минимум потерь, связанных с неточностью определения экстремума. Следовательно, САО не эффективно решает задачу экстремального регулирования. Таким образом, существует три задачи, которые должны решаться при разработке САО в условиях неопределенности: - задача компенсации высокочастотных возмущений; - задача обнаружения и устранения низкочастотных возмущений, с целью обнаружения и устранения дрейфа характеристики, что обеспечивает устойчивость и требуемую точность САО; - задача компенсации инерционности ОУ. Решение задачи компенсации возмущений требует анализа статистических характеристик возмущений и выявления параметров объекта, на основе которых формируется показатель качества. При разработке САО инерционного объекта следует применять методы моделирования ОУ в условиях неполноты данных и алгоритмы оптимизации для оценки состояния ОУ. Классификация видов неопределенности. Известна следующая классификация неопределенностей, иллюстрированная на рис. 4.4.3. Рис. 4.4.3 Неполнота информации относительно вида и параметров экстремальной характеристики ОУ достаточно часто существует при разработке САО. Если информация неполная, что являются следствием недостаточного знания особенностей функционирования объекта, то данная неопределенность в процессе функционирования САО должна быть устранена. Физическая неопределенность обусловлена несовершенством устройств измерения и погрешностями управляющих устройств. Случайность характеризуется вероятностной и возможностной мерой. Если некоторому значению параметра соответствует подмножество в области определения, не являющееся одноточечным, то такое значение называется неточным. Неточность связывается с возможностной мерой или определена вербальными понятиями. При работе с неточными значениями используется теория вероятностей, теория возможностей, интервальный анализ, теория ошибок. Рис 4.4.4 Лингвистическая неопределенность появляется при описании экспертами параметров и правил функционирования ОУ, получения управляющих решений средствами естественного языка. В этом случае применяют методы из теории нечетких множеств и нечеткой логики на основе лингвистической переменной. Так как алгоритм оптимизации – последовательная процедура принятия решений и процедура формирования управляющих воздействий на ОУ, то формирование управляющих воздействий осуществляется путем получения информации (пробные шаги) и формированием рабочих шагов, т. е. движение к экстремуму. Применение детерминированных алгоритмов принятия решений при четких данных. Предполагается, что модель ОУ адекватна и достаточно полная. В этих условиях САО имеют (теоретически) максимальное быстродействие, но неустойчива по отношению к внешним возмущениям и помехам. Структура САО с детерминированными алгоритмами показана на рис. 4.4.5. Рис. 4.4.5 Применение нечетких алгоритмов с четкими параметрами объекта и значениями измерений характеристик. Данный вид САО – системы с переменными параметрами. В САО применяется нечеткая процедура выбора рабочего шага поиска (последовательный алгоритм принятия решений). На рис. 4.4.6 показана структура САО с нечеткими алгоритмами. Рис. 4.4.6 Система одновременно является САО с детерминированной или статистической процедурой принятия решений и в системе производится выбор параметров алгоритмов поиска экстремума на основе данных анализа текущей ситуации с применением блока выбора параметров алгоритмов. Выбор параметров происходит с применением экспертных знаний. В качестве ситуационной модели могут быть применены модели нечеткого логического вывода или анализа нечетких ситуаций. Применение нечеткихправил принятия решений с нечеткими критериями качества. Данный вид САО – нечеткие системы принятия решений и с переменными параметрами. Критерий качества задан в виде нечеткой функции. Также нечетко заданы и параметры ОУ. Примерная структура САО показана на рис. 4.4.7. Рис. 4.4.7 Данный вид САО можно назвать нечеткой система экстремального управления и эта система является обобщением рассмотрен выше систем с применением статистических методов принятия решений, детерминированных алгоритмов принятия решений при четких данных, а также систем с нечеткими алгоритмами с четкими параметров объекта и значениями измерений характеристик. Использование нечетких критериев качества, параметров ОУ и методов принятия решения на основе нечетких логических правил вывода позволяет расширить область применения экстремальных систем, делает необходимым исследование системы подобного вида. Системой автоматической оптимизации называется система автоматического управления, целью функционирования которой является поиск величин управляющих воздействий, при которых достигается экстремум показателя качества системы. Управляющим решением в САО называется изменение вектора входных координат ОУ с целью достижения экстремума. Поисковой стратегией САО называется совокупность правил выбора управляющих решений для каждой ситуации функционирования САО. Эффективность поисковой стратегии оценивается набором критериев, включающим критерии точности и быстродействия. Поиск оптимальных величин входных воздействий можно представить как совокупность этапов, направленных на разрешение неопределенности относительно эффективности функционирования ОУ и выбор управляющих решений: - этап 1. Процесс получения достоверной информации; - этап 2. Выбор оптимального управления для достижения цели поиска. Этап 1 связан с получением достоверной информации о положении рабочей точки ОУ относительно экстремального значения по данным измерения выходной величины ОУ (экстремальной характеристики) путем анализа реакции ОУ на пробные возмущения. Этап 2 связан с выбором поисковой стратегии и применением этой стратегии при поиске экстремума (выборе рабочего движения САО). Основные требования на этапе 1 связаны с тем, что процедура получения информации должна обеспечивать: - помехоустойчивость системы (снижение частоты ложных срабатываний); - быстродействие системы (реакцию на изменение состояния); - компенсацию переходных процессов в ОУ при наличии существенной инерционности; - наименьшее возможное воздействие на ход нормального функционирования ОУ; Требования помехоустойчивости и быстродействия являются противоречивыми. Поэтому решение данной задачи связано с выбором из множества допустимых алгоритмов. Основные требования на этапе 2 связаны с тем, что поисковая стратегия должна обеспечивать: - минимизацию времени затрачиваемого на поиск экстремума; - минимальное воздействие на процесс нормального функционирования ОУ; - уменьшение риска связанного с принятием неверного решения. Решение данной задачи связано с применением гибких поисковых стратегий, основанных на адаптивных процедурах выбора параметров САО. Для решения задачи выбора режимов работы и поисковых стратегий САО должна обладать средствами оценки процесса функционирования, предоставляющими информацию в виде различных критериев позволяющих реализовать адаптивное поведение САО.
|
||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |



 , (4.4.2)
, (4.4.2) , (40.3)
, (40.3) , zt Î Z с n координатами
, zt Î Z с n координатами  состояния ОУ.
состояния ОУ. , xt Î X влияющий на показатель качества. Входное воздействие задает режим функционирования ОУ и определяется вектором
, xt Î X влияющий на показатель качества. Входное воздействие задает режим функционирования ОУ и определяется вектором  , ltÎ L. Входное воздействие не является оптимизируемым параметром.
, ltÎ L. Входное воздействие не является оптимизируемым параметром.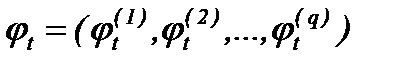 , jt Î J.
, jt Î J. ‑ множество выходных переменных ОУ, элементы которого, согласно (9.3), y t =Q (z t ,x t ,j t) – функции параметров z t ,x t ,j t, т.е. выходные параметры рассматриваются, как различные критерии качества функционирования ОУ в результате управления.
‑ множество выходных переменных ОУ, элементы которого, согласно (9.3), y t =Q (z t ,x t ,j t) – функции параметров z t ,x t ,j t, т.е. выходные параметры рассматриваются, как различные критерии качества функционирования ОУ в результате управления.


