
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача адаптации САО возникает в следующих случаях.Содержание книги
Поиск на нашем сайте
1. Крутизна характеристики объекта либо неизвестна, либо известна неточно или может меняться в значительных пределах в зависимости от состояния (режима) ОУ. 2. Статистические характеристики измерений показателя качества при разработке или настройке САО неизвестны или определены неточно. 3. Модель динамики ОУ по каналу оптимизации известна лишь приближенно. Идентификация модели характеристики возможна только для объектов функционирующих в стационарных режимах. Идентификация модели характеристики связана с проведением экспериментов на ОУ с возможным нарушением режима нормального функционирования. В этом случае целесообразно интегрировать процедуру идентификации модели характеристики в поисковый алгоритм. Если для объекта по разным причинам невозможно построить модель характеристики, обеспечивающую требуемую точность решения экстремальной задачи, то могут быть применены методы адаптации САО к параметрам текущей ситуации. Определение статистических характеристик измерений показателя качества может быть произведено на функционирующем ОУ. Если эти характеристики остаются постоянными при изменении режима функционирования, то можно использовать методы синтеза статистически оптимальных поисковых процедур. Если же возможно изменение характеристик измерений, то необходима процедура идентификации статистических характеристик в составе САО. Построение модели динамики показателя качества требует дополнительных знаний о структуре ОУ. Решением задачи может быть предположение относительно структуры модели динамики с последующей идентификацией коэффициентов модели до начала работы САО или применением методов адаптации модели динамики в процессе работы САО. Адаптивный подход к построению САО позволяет разрабатывать системы управления и оптимизации в условиях частичной априорной неопределенности относительно свойств объекта или процесса. Отличительным свойством адаптивной САО является наличие средств получения апостериорной информации в процессе функционирования системы «ОУ – САО» и использования этой информации для улучшения характеристик функционирования системы. Возможны следующие уровни адаптации системы поисковой оптимизации: - адаптация параметров САО; - адаптивная модель экстремальной характеристики; - адаптация базы знаний (стратегий) САО. Адаптация параметров предполагает наличие средств оценки эффективности функционирования САО и не требует информации о параметрах экстремальной характеристики. В процессе функционирования определяются такие значения коэффициентов настройки САО, при которых достигается цель. Применение методов идентификации модели характеристики позволяет использовать информацию о связи между параметрами настройки САО и параметрами характеристики ОУ. Адаптация базы стратегий поиска предполагает наличие средств оценки эффективности применяемых стратегий поиска и корректировку базы алгоритмов. В монографии рассматривается преимущественно второй метод построения адаптивной САО. Можно выделить следующие направления в построении адаптивных систем экстремального регулирования на основе последовательных процедур статистической проверки гипотез. Адаптация к неизвестным статистическим характеристикам. Идентификация распределения вероятностей и его параметров в процессе работы системы позволяет улучшить точность и быстродействие САО со статистическими процедурами принятия решений. Расширение множества принимаемых решений. Число гипотез в процедуре принятия решений определяется числом оцениваемых состояний системы. Пусть Hk – гипотеза относительно k -го состояния системы. Принятие гипотезы Hk соответствует выбору действия uk. Действие состоит в выборе величины и направления шага поиска. При наличии дополнительной информации решение в САО может быть принято досрочно, т.е. используется усеченная процедура проверки гипотез. При этом можно ввести характеристику возможности принятия неверного решения m (uk) и используя распределение возможностей на множестве принимаемых решений построить схему выбора действия. Чем больше возможность неверного решения, тем осторожнее должно быть поведение системы. Схема выбора действия представляет собой стратегию поиска, которая в этом случае зависит от конкретного объекта. Повышение информационной емкости пробных возмущений. САО со статистическими процедурами принятия решений требуют для работы только информацию о знаке или величине приращения характеристики. В случае высокой стоимости проб или больших затратах времени на измерение показателя качества для повышения эффективности САО необходимо использовать дополнительную информацию, которая может быть получена при анализе реакции на пробные воздействия. Оценка приращения характеристики на k –м шаге поиска может быть расширена следующим образом. Пусть yki=<I1,I2,…,Iq> ‑ оценка показателя качества, рассматриваемая как совокупность свойств. При отсутствии дополнительной информации yki=<I1> ‑ величина показателя качества. Свойствами оценок являются: - I 1 = y – величина показателя качества; - I 2= x – значение входной координаты при котором выполнено измерение; - I 3= t – время измерения; - I 4=D y t – дрейф показателя качества; - I 5= s – разброс (дисперсия) значений. Также может фиксироваться вектор состояния ОУ, при котором было произведено измерение y ki. Существующие последовательные процедуры имеют ряд ограничений: - учитываются только величина показателя и разброс значений, причем статистические характеристики предполагаются постоянными; - алгоритмы последовательного анализа рассчитаны на повторение проб в фиксированной рабочей точке и не рассчитаны на анализ случайных блужданий системы. Для построения алгоритмов с использованием дополнительной информации могут быть использованы методы классификации на основе теории нечетких множеств и математической статистики. Существующие последовательные процедуры имеют ряд ограничений: - учитываются только величина показателя и разброс значений, причем статистические характеристики предполагаются постоянными; - алгоритмы последовательного анализа рассчитаны на повторение проб в фиксированной рабочей точке и не рассчитаны на анализ случайных блужданий системы. Для построения алгоритмов с использованием дополнительной информации могут быть использованы методы классификации на основе теории нечетких множеств и математической статистики. Использование оптимизационной модели объекта. Для технических объектов, функционирующих в условиях малых или медленно меняющихся неконтролируемых возмущений, может быть построена модель, связывающая значения входных ситуационных параметров ОУ и значений оптимизируемых параметров ОУ, при которых достигается экстремум. Такая модель, называемая еще режимной оптимальной картой, позволяет исключить поиск на объекте. Необходимость поиска зависит от точности режимных карт, числа учитываемых значимых параметров и возможности адаптации режимных карт к изменению свойств ОУ во времени. При этом САО функционирует в контуре адаптации системы управления. Использование идентифицируемой модели экстремальной характеристики. Для выбора параметров алгоритмов САО необходима информация о виде и параметрах экстремальной характеристики. Экстремальная характеристика может быть аппроксимирована некоторой функциональной зависимостью с неизвестными параметрами. Идентификацию параметров этой модели целесообразно осуществлять по данным предыстории функционирования ОУ, а также в режиме нормального функционирования. Проведение экспериментов на ОУ для этой цели требует нарушения режима нормального функционирования и во многих случаях недопустимо. Поэтому модель экстремальной характеристики будет характеризоваться неполнотой информации. Целесообразно использовать принцип адаптивного управления с идентификатором в цепи обратной связи при построении адаптивной САО. Для представления неполной или неточной информации с возможностью уточнения в процессе функционирования, и для принятия решений в САО могут быть использованы нечетко-вероятностные модели, основанные на нечетких и лингвистических оценках параметров. Классификация поисковых стратегий. Стратегия поиска определяет направление и амплитуду серии поисковых воздействий на ОУ в зависимости от результата влияния предшествующих поисковых воздействий на состояние ОУ с целью достижения экстремального значения характеристики за минимально возможное время. Если x – вектор оптимизируемых параметров, uk – управляющее решение на k -шаге оптимизации, то стратегия поиска в шаговой САО есть правило выбора Dxk, такого что xk+1=xk+Dxk при условии что система находилась в состоянии xk и было принято управляющее решение uk. Поисковые стратегии можно классифицировать на детерминированные, случайные и нечеткие. Детерминированные стратегии поиска однозначно связывают предшествующее состояние ОУ и последующее воздействие на ОУ. Детерминированные стратегии используются при минимальной априорной информации или высоком уровне помех, не позволяющем оценить параметры характеристики ОУ. Случайные стратегии поиска предполагают выработку случайных воздействий на ОУ по определенным алгоритмам с целью достижения экстремума. Областью применения случайных поисковых стратегий являются ОУ с характеристикой сложной формы, имеющей локальные экстремумы. Нечеткие стратегии поиска представляют собой нечеткие алгоритмы или правила выбора поисковых воздействий, в которых учитывается специфика знания ОУ Нечеткие стратегии отличаются многовариантностью выбора управляющих решений, применяются в условиях нечеткости исходной информации с возможностью последующего ее уточнения. Результаты сравнения стратегий приведены в табл. 4.4.1. Таблица 4.4.1
Выбор стратегии поиска определяется видом экстремальной характеристики ОУ, наличием инерционности ОУ, наличием модели характеристики и информации о значениях параметров этой модели, а так же режимом работы ОУ, наличием и степенью дрейфа характеристики. Существующие стратегии поиска различают по требуемой априорной информации. Рассмотрим для примера следующие известные стратегии поиска экстремума. Стратегия с постоянным шагом поиска. Для любого значения x (k) определяется D x k= a = const. Эта стратегия требует минимальной дополнительной информации и может быть использована при неизвестных значениях параметров модели экстремальной характеристики. Стратегия с адаптивным шагом. Учитывается предыстория управляющих решений, характер преимущественного движения САО u k =< u k, u k - 1, …, u k-L >. При этом D x k= a k= f (D x k‑1, u k). Возможны и другие способы адаптации шага поиска. Стратегии поиска с адаптивным шагом эффективны в окрестности экстремального значения при малой крутизне характеристики, но при отработке ступенчатых возмущений возможно значительное перерегулирование при обнаружении экстремума. Стратегия поиска с экстраполяцией. Если известен вид и параметры экстремальной характеристики y = Q (x), то по известной оценке приращения характеристики D y k определяется точным или приближенным методом величина D x k так, чтобы точка x k+1= x k+D x k соответствовала положению экстремума. Существует множество стратегий поиска с экстраполяцией. Недостатком систем с экстраполяцией является низкая помехоустойчивость. Стратегии с экстраполяцией эффективны при наличии достаточно точной модели экстремальной характеристики и точных оценках градиента характеристики. Стохастическая аппроксимация. Процедуры стохастической аппроксимации (алгоритмы Кифера-Волфовитца) используются для нахождения экстремума ограниченной унимодальной функции на заданном интервале, наблюдаемой на фоне шума с ограниченной дисперсией. Алгоритм заключается в формировании последовательности
которая сходится к экстремальному значению x opt с вероятностью 1 при соответствующем выборе последовательности g k. Методы стохастической аппроксимации в исходной постановке не удовлетворяют требованиям практики: не обеспечивается быстродействие поиска, не учитывается ситуация поиска и дрейф характеристики. Требования к точности модели и измерений показателя качества для этого класса стратегий ниже, чем для экстраполяционных методов. Случайный поиск. Алгоритм случайного поиска заключается в выборе величины D x k случайным образом: D xk=±ax, где x – единичный случайный вектор. Простейшим алгоритмом случайного поиска является поиск с парными пробами, в котором входное воздействие выбирается по формуле x k+1= x k – a x sign [ Q (x k+ gx) – Q (x k- gx)], что соответствует задаче поиска минимума показателя качества. Случайный поиск допускает неоднозначность результата при одинаковых исходных данных и в этом состоит отличие рандомизированных стратегий поиска от всех остальных методов, включая нечеткие стратегии. Исследования показывают, что случайный поиск эффективен для многоэкстремальных объектов, в САО с большим числом регулирующих воздействий. Нечеткие стратегии. Правило выбора управляющего воздействия в поисковой системе может быть определено в общем виде как
где uk – предыстория управляющих решений, xk – предыстория управляющих воздействий. Нечеткое правило управления может быть задано как нечеткое множество правил управления
с функцией принадлежности
где Эвристические стратегии. Правила выбора управляющих решений, основанные на опыте эксплуатации систем управления и оптимизации представляют собой эвристические стратегии поиска. Эвристические методы предполагают изучение принципов переработки информации человеком при решении задач и моделирование процессов решения в управляющей системе. Эвристические решения используются, когда строгий алгоритм решения задачи отсутствует или информация необходимая для решения недостаточна. В процессе поиска решения иногда производят дополнительный сбор необходимой информации. Эффективность подобных стратегий не может быть строго доказана, но может быть подтверждена опытом эксплуатации систем или при исследовании соответствующих стратегий на имитационной модели. Аппарат нечетких множеств является средством формализации эвристических стратегий. Минимально необходимая информация для любой стратегии представляет собой сведения о знаке приращения характеристики. В табл. 4.4.2. приведена дополнительная информация, необходимая для работы каждого из рассмотренных выше типа стратегий. Таблица 4.4.2
Алгоритмы нечеткой стохастической аппроксимации. Методы поиска с экстраполяцией предполагают, что характеристика объекта может быть аппроксимирована некоторой функцией оптимизируемых параметров. В реальных условиях коэффициенты такой модели могут быть определены лишь приближенно, что не позволяет применить точные методы экстраполяции, но могут быть использованы эвристические правила поиска. Пусть рабочая точка находилась в окрестности оптимального значения и произошло ступенчатое смещение характеристики (изменение режима) и величина градиента характеристики увеличилась, или известно, что рабочая точка не находится в окрестности оптимального значения. Время достижения оптимального значения будет определяться процедурой выбора рабочего шага, при этом система может не достигнуть экстремума за один шаг поиска. Использование модели характеристики позволяет реализовать следующий алгоритм выбора рабочего шага. Шаг 1. Оценить величину градиента характеристики Шаг 2. Выбрать величину рабочего шага которая возможно переведет систему снова в экстремум или повысит скорость поиска, при соблюдении ограничений. Шаг 3. Выполнить шаг. Шаг 4. Оценить величину градиента характеристики. Шаг 5. Если ситуация сохраняется, перейти к п. 2. иначе к п. 6. Шаг 6. Значительно уменьшить шаг (минимум в 2 раза). Шаг 7. Применить стратегию с адаптивным шагом. Выбор величины рабочего шага по градиенту характеристики может быть осуществлен на основе нечеткой модели, учитывающей риск, связанный с принятием неверного решения. Требуемая априорная (экспертная) информация: вид характеристики и приближенные значения ее параметров; ограничения на изменение управляемых переменных. Требуемая апостериорная информация: оценка градиента на текущем шаге, оценка градиента на предыдущих шагах для сравнения и определения значимого изменения; достоверные сведения о том, что система не находится в окрестности экстремального значения. Рассмотренный алгоритм представляет собой поисковую процедуру с нечеткой экстраполяцией или нечеткой стохастической аппроксимацией. Отличие этого алгоритма от детерминированных процедур состоит в возможности учета данным алгоритмом достоверности информации о ситуации поиска. На шаге 2 в зависимости от наличия необходимой информации стратегия поиска представляет собой стратегию с постоянным шагом, стратегию стохастической аппроксимации или стратегию экстраполяции. В процессе работы система переходит к стратегии с адаптивным шагом поиска в окрестности экстремума. Алгоритм с измерением знака приращения характеристики. Для случая статической характеристики объекта f (x, t)= f (x) и случайного процесса j (t), аддитивного к измерению выходной величины объекта, с характеристиками M [ j (t)]=0, K j(t 1, t 2)=0 при t 1¹ t 2, D [ j (t)]= s 2 (4.4.10) можно построить алгоритм САО, основанный на последовательной процедуре проверки статистических гипотез. При дальнейшем рассмотрении будем полагать, что характеристика объекта f (x, t) имеет максимум в точке x = x max. В случае, если характеристика имеет минимум, метод легко модифицируется. Пусть на вход объекта с постоянным интервалом (t i+1- t i) подаются пробные ступенчатые смещения x 1i= x (t 2i)= x 0+ g, x 2i= x (t 2i+1)= x 0- g, i =0,1,…, n -1, где x 0 – положение рабочей точки, g – величина пробного смещения. Получены измерения выходного сигнала y 1i= f (x 1i), y 2i= f (x 2i), как показано на рис. 4.4.8.
Рис 4.4.8 Исходом эксперимента будет случайная величина z, принимающая значения
При указанных условиях (4.4.11) вероятность появления z i=1 будет постоянна и равна p и зависит от положения рабочей точки и вида характеристики. Распределение величины z предполагается биномиальным с параметром p, значение которого неизвестно. Рассмотрим альтернативные гипотезы H 1 и H 0 того, что величина z имеет биномиальное распределение с параметром p 1 и p 0 соответственно, p 1> p 0. Поскольку необходимо определить положение рабочей точки на правой или на левой ветви характеристики, то выбираем значения параметров p 1>0,5 (рабочая точка на левой ветви) и p 0<0,5 (рабочая точка на правой ветви). Пусть f (z, p) – распределение величины z с оцениваемым параметром p. Вероятность получения выборки (z 1, z 2, …, z n) равна p 1n= f (z 1, p 1) f (z 2, p 1)… f (z n, p 1) при p = p 1 и p 0n= f (z 1, p 0) f (z 2, p 0)… f (z n, p 0) при p = p 0. На каждой стадии эксперимента проверяется отношение p 1n/ p 0n. Выбираем величины A и B, такие, что если на некоторой стадии эксперимента p 1n/ p 0n³ A, то процесс оканчивается принятием гипотезы H 1; если p 1n/ p 0n£ B, то принимается гипотеза H 0; иначе эксперимент продолжается. Показано, также, что величины A и B следует выбирать, исходя из соотношений: A £(1− b)/ a, B ³ b /(1− a), (4.4.12) где a − вероятность ошибки первого рода (отклоняется истинная гипотеза H 0), b − вероятность ошибки второго рода (принимается гипотеза H 0, тогда как истинной является H 1). Правило принятия решения имеет вид:
где
Рассмотренный критерий часто называют биномиальным. Алгоритм с измерением знака и величины приращения характеристики. Рассмотренный выше алгоритм не учитывает величину изменения характеристики в рабочей точке, а ограничен рассмотрением знака этого изменения. Если допустить, что случайный процесс j (t)º j и любое сечение распределено нормально с плотностью x (j, 0, s), то можно построить критерий, учитывающий величину градиента характеристики в рабочей точке. Пусть имеются две гипотезы H 0: q = q 0, H 1: q = q 1, q - неизвестное среднее значение величины d, распределенной нормально с дисперсией s b 2. Исходом эксперимента будет случайная величина z, принимающая значения
где
q 1, q 0 – некоторые параметры, q 1 > q 0, выбор значений которых зависит от используемой оценки величины d (рис. 4.4.9a) или (рис. 4.4.9б), а так же от вида характеристики и необходимого быстродействия. В этом случае
Правило принятия решения имеет вид:
Коэффициенты A, B определяются соотношениями (4.4.12).
Рис 4.4.9.а Рис 4.4.9.б Подобный алгоритм не только обладает адаптивными свойствами, но и позволяет корректировать параметры q 1, q 0 в процессе поиска. Оценка (4.4.9) позволяет реализовать последовательный метод на базе градиентных методов с парными и односторонними пробами. Для метода с парными пробами последовательная процедура с накоплением оценок D y впервые известна. При этом xi определяется согласно (4.4.16) и, при n -кратном измерении можно получить: M [ nd i]= n D y, Из (4.4.17) следует, что при многократном определении D y уровень полезного сигнала увеличивается быстрее уровня помехи, что дает возможность при больших n снизить влияние возмущений. Если q 0=- q 1=2 kg, где k >0 – модуль градиента характеристики, то правило принятия решения имеет вид:
где P – вероятность ошибки определения знака градиента. Среднеквадратичное отклонение помехи s оценивается по результатам испытаний, либо задается экспертом. Оценка характеристик последовательных алгоритмов. Оценка характеристик биномиального критерия. Существуют методы оценки быстродействия алгоритма САО, основанного на последовательной процедуре. Предлагаются соотношения для определения среднего числа наблюдений при последовательном критерии для случая биномиального распределения:
где
здесь h (p) находится из соотношения
для заданных p 1, p 0 и известного значения p. Величина E n(p) определит среднее число наблюдений для принятия решения и может быть использована при выборе значений пробного шага и порогов p 1, p 0. L (p) называется оперативной характеристикой критерия и определяет вероятность принятия гипотезы H 0 при истинном значении параметра p. В рассматриваемом случае истинное значение параметра p зависит от положения рабочей точки, p = p (x 0). Можно определить вероятность ошибочного решения при условии, что x = x 0. Ошибочным будет решение принять гипотезу H 0, если x 0< x max или принять гипотезу H 1 при x 0> x max. Вероятность ошибочного решения выражается через оперативную характеристику следующим образом:
При заданных значениях параметров p 1, p 0 значение координаты, в которой достигается экстремум, может не совпадать с точкой равновесия системы поиска с последовательной процедурой, определяемой из условия L (p (x))=0,5. (4.4.22) В некоторых случаях значение p (x) может быть вычислено достаточно просто. При условиях (4.4.4) j (t) º j, плотность вероятности любого сечения случайного процесса не зависит от t и равна x (j). Вероятность того, что случайная величина z (4.4.5) примет значение z = 1 определится как p (x 0)= P {[ y (x 0+ g)+ j (t)]–[ y (x 0– g)+ j (t + t)]³0}, или p (x 0)= P {[ j (t + t)− j (t)]£D y }, D y = y (x0+ g)− y (x 0− g). Если известна плотность распределения сечения x ( j ), то p (x 0) определится:
Если величина j имеет нормальный закон распределения N (0, s), то
Соотношения (4.4.22), (4.4.23) и (4.4.24) позволяют определить среднее число испытаний и вероятность ошибки при принятии решения при любом допустимом значении x = x 0. На рис. 4.4.9.а и 4.4.9.б. приведены сравнительные характеристики поисковой процедуры без фильтрации и с фильтрацией. Для градиентного метода с одним испытанием вероятность ошибки p e(x)=1− p (x). Таким образом, любая процедура принятия решения, для которой p e(x)<1− p (x) для всех допустимых значений x, будет эффективнее градиентного метода с единичным экспериментом по критерию p e, но при этом, очевидно, существует оптимальная процедура по критерию E n. Оценка характеристик нормального критерия. Для алгоритма с оценкой (4.4.15) оценка среднего числа наблюдений определяется из формулы (4.4.17), где p º q,
L (q) определяется по формуле (4.4.18), где p º q,
Вероятность ошибочного решения p e(x) может быть определена по формуле (4.4.22). Вероятность p (x)= P {D y >0} может быть определена по формуле (4.4.22). Если дисперсия известна неточно, т. е. s как параметр последовательного критерия не совпадает с действительным значением дисперсии оценки s *, то для любого априори заданного значения s характеристики последовательного критерия определятся как
Выбор параметров алгоритмов САО следует производить так, чтобы выполнялось соотношение p e(x)<1− p (x). Следует учитывать тот факт, что уменьшение p e(x) сопровождается ростом среднего числа наблюдений и в точке x 0, сколь угодно близкой к оптимальному значению параметра, среднее число наблюдений E n(p) значительно возрастает. Чтобы обеспечить достаточное быстродействие алгоритмов вблизи экстремума при малой величине градиента характеристики и высоком уровне шума применяются различные модификации рассмотренных алгоритмов. Нечеткая модификация последовательных алгоритмов САО. Параметры p 0, p 1 в гипотезах, рассматриваемых в алгоритмах САО, являются четкими величинами, выбор которых зависит от априорных сведений относительно вида характеристики и случайных возмущений. В отсутствии, при неполноте или неточности таких сведений эти параметры будут являться нечеткими величинами. Рассмотрим нечеткие гипотезы
где p 1, p 0 – нечеткие числа с функциями принадлежности m i(p), i =1, 2. Предложено использовать функции принадлежности следующего вида
d – параметр, характеризующий расплывчатость априорной информации. Если задать значение m = m *, то для любой унимодальной функции принадлежности m i(p) можно определить два значения p i(1), p i(2) и рассмотреть совокупность из девяти четких гипотез, образованных парами (p 1(i), p 2(j)), I, j =0, 1, 2. Пусть z – параметр принятия решения в выбранном алгоритме САО (последовательном критерии). Для биномиального алгоритма z º m, m – число успешных испытаний (см. выше). Для нормального критерия z º
Для нечетких гипотез можно построить соответствующие уравнения нечетких порогов принятия каждой из нечетких гипотез. Пороги принятия решения определяются следующими выражениями: Возможны и другие способы формирования порогов областей принятия решения. Для сравнения можно рассмотреть выбор области минимальной и максимальной площади по заданному m –срезу нечетких оценок параметров. Область минимальной площади (MIN-область) формируется по значениям параметров p 1= max {p1(i)}, p0=min{ p 0(j)}, I,j =0, 1, 2. Область максимальной площади (MAX-область) формируется по значениям параметров p 1= min { p 1(i)}, p 0= max { p 0(j)}, I, j =0, 1, 2. Выбор метода разрешения неопределенности зависит от требований задачи. На рис. 4.4.10.а и 4.4.10.б приведены сравнительные характеристики поисковой процедуры при различных методах разрешения неопределенности. Точное значение соответствует выбору m =1.
Рис 4.4.10.а Рис 4.4.10.б Выбор наиболее предпочтительного метода разрешения неопределенности требует проведения дополнительных исследований. Сокращение числа пробных испытаний при неполноте сведений о характеристике ОУ целесообразно при использовании методов идентификации характеристики, позволяющих разрешить неопределенность относительно параметров характеристики ОУ. Для определения коэффициентов нечеткой модели целесообразно использовать экспертные оценки параметров, базирующиеся на расчетах по методам теории последовательного анализа при известных допущениях относительно статистических свойств случайных возмущений, с последующей проверкой на имитацонной модели САО.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.011 с.) |

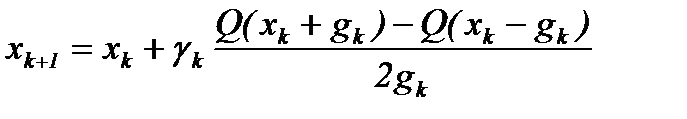 , (4.4.7)
, (4.4.7)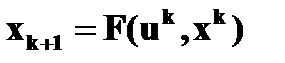 ,
,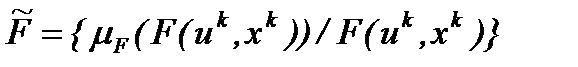 (4.4.8)
(4.4.8)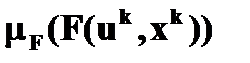 определенной на базовом множестве правил
определенной на базовом множестве правил 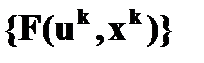 . Нечеткой стратегией называется тройка
. Нечеткой стратегией называется тройка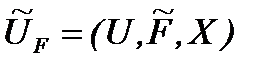 , (4.4.9)
, (4.4.9)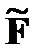 - нечеткое правило. Введение нечетких стратегий оправдано при оптимизации систем с априорной неопределенностью. Понятие нечеткой стратегии обобщает известные поисковые стратегии и позволяет выбирать наиболее эффективные правила управления в процессе работы системы, т. е. является базовым средством для разработки адаптивных поисковых систем. Правило F представляет собой элементарную стратегию поиска.
- нечеткое правило. Введение нечетких стратегий оправдано при оптимизации систем с априорной неопределенностью. Понятие нечеткой стратегии обобщает известные поисковые стратегии и позволяет выбирать наиболее эффективные правила управления в процессе работы системы, т. е. является базовым средством для разработки адаптивных поисковых систем. Правило F представляет собой элементарную стратегию поиска.
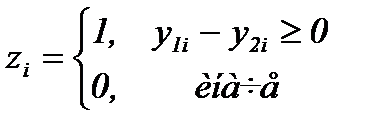 . (4.4.11)
. (4.4.11)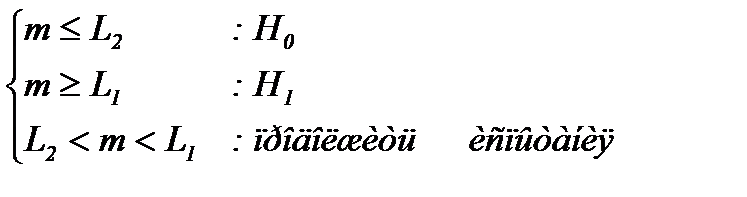 , (4.4.13)
, (4.4.13)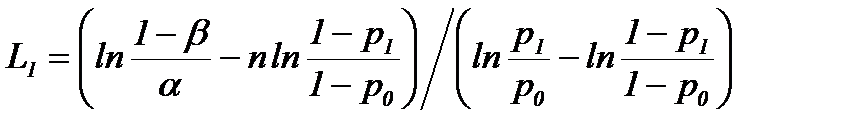 ,
, 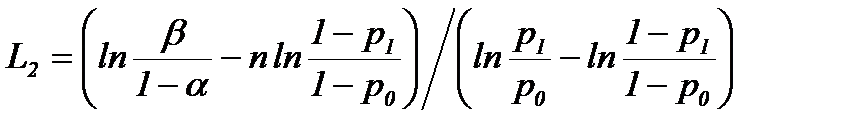 .
.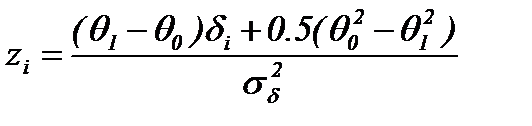 , (4.4.14)
, (4.4.14)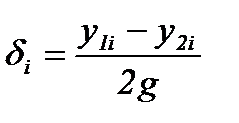 , sd=
, sd= 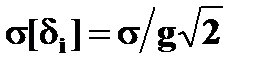 , либо
, либо 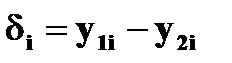 , sd=
, sd= 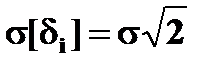 ,
,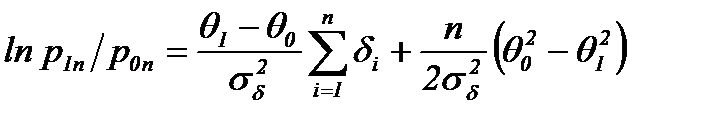 . (4.4.15)
. (4.4.15)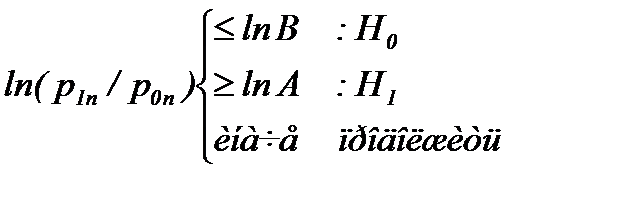 . (4.4.16)
. (4.4.16)

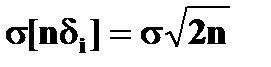 . (4.4.17)
. (4.4.17)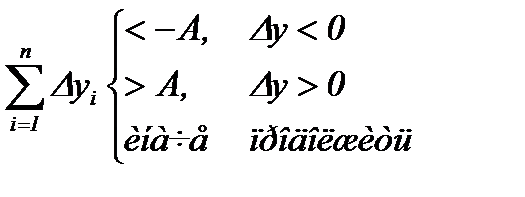 , (4.4.18)
, (4.4.18)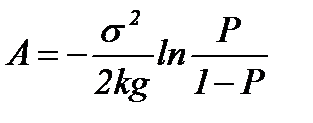 , (4.4.19)
, (4.4.19)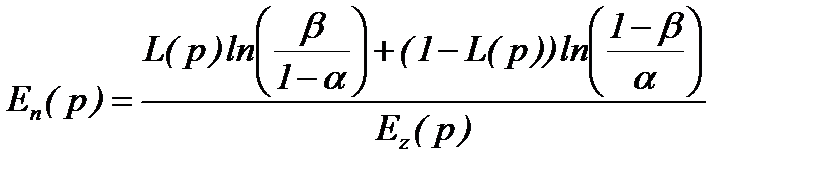 , (4.4.20)
, (4.4.20)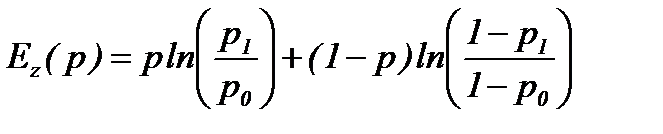 ,
, 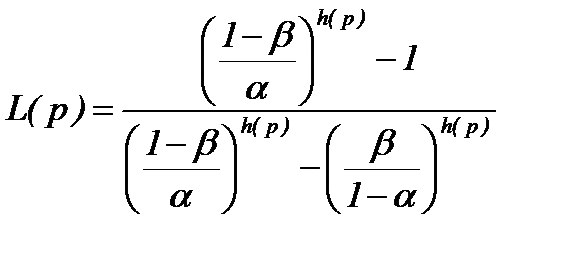 ,
,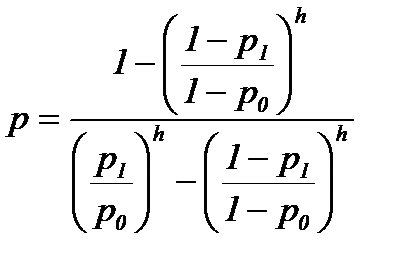
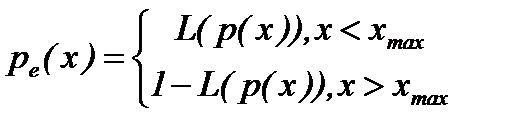 (4.4.21)
(4.4.21)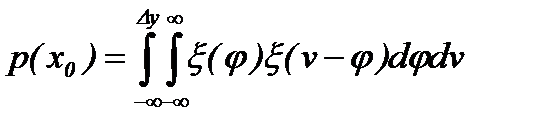 (4.4.23)
(4.4.23)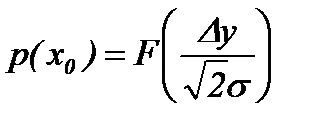 . (4.4.24)
. (4.4.24)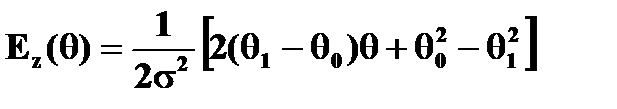 ,4.4
,4.4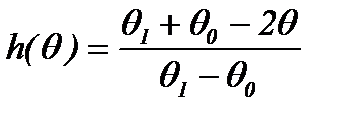 .
.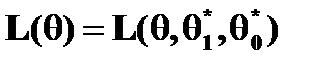 ,
, 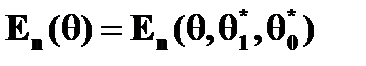 ,
,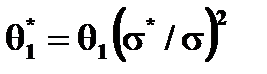 ,
, 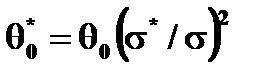 . (4.4.25)
. (4.4.25)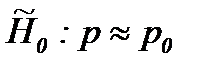 ;
; 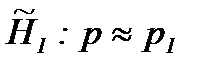 , (4.4.26)
, (4.4.26)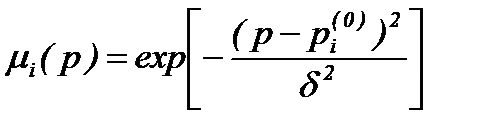 , i =0, 1, (4.4.27)
, i =0, 1, (4.4.27)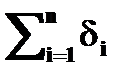 , d I – оценка приращения характеристики (см. выше). Для последовательного критерия всегда можно определить уравнения порогов L 1, L 2 принятия гипотез, такие, что
, d I – оценка приращения характеристики (см. выше). Для последовательного критерия всегда можно определить уравнения порогов L 1, L 2 принятия гипотез, такие, что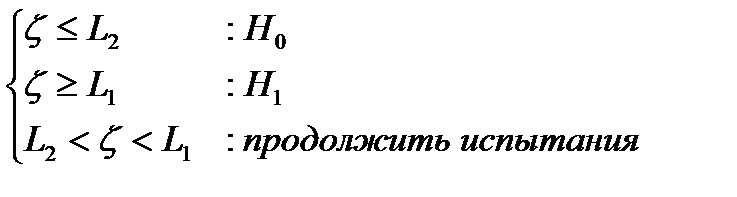 . (4.4.28)
. (4.4.28)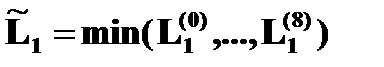 ,
, 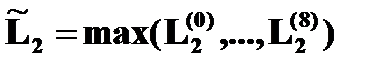 . Известно, что такой подход может увеличить быстродействие системы поиска за счет сокращения площади области продолжения испытаний. При указанном принципе формирования порогов при неточности исходной информации точность отслеживания экстремума должна снижаться, а скорость реакции на изменение характеристики ОУ – повышаться.
. Известно, что такой подход может увеличить быстродействие системы поиска за счет сокращения площади области продолжения испытаний. При указанном принципе формирования порогов при неточности исходной информации точность отслеживания экстремума должна снижаться, а скорость реакции на изменение характеристики ОУ – повышаться.




