Элементарные звенья систем автоматического управления

Общие характеристики

Техническими элементами систем автоматического и автоматизированного управления технологическим оборудованием являются средства получения, преобразования и регистрации первичной информации, а также аналоговые и цифровые вычислительные средства и исполнительные устройства.

Средства получения, преобразования и регистрации первичной информации – это датчики и вторичные приборы (непрерывные – аналоговые и дискретные).

К аналоговым средствам относятся датчики непрерывного действия, усилители, аналоговые вычислительные машины (АВМ), исполнительные устройства и регуляторы непрерывного действия.

Исполнительными устройствами являются технические элементы, оказывающие непосредственное физическое воздействие на технологические процессы (ТП).

При рассмотрении общих характеристик технических элементов считается, что любой из них можно представить как преобразователь входного сигнала x в выходной y. Тогда любой элемент реализует некоторую функциональную зависимость преобразования вида y=F (x).

Любой элемент или систему автоматики можно характеризовать следующими главными показателями: коэффициентом преобразования, погрешностью, порогом чувствительности, степенью устойчивости и колебательностью. Первые три показателя качества называют прямыми, а два последних – косвенными. К прямым показателям также относят быстродействие, а применительно к регуляторам – время регулирования и величину перерегулирования.

К косвенным показателям качества систем автоматического управления и регулирования (САУ и Р) относят корневые показатели (степень устойчивости и колебательности), частотные (устойчивость по амплитуде и запас устойчивости по фазе) и интегральные (квадратичные интегральные) оценки.

1. Коэффициент преобразования – это отношение выходной величины ко входной

k=y / x

(2.8.1)

или отношение их приращений

k’ =Δ y /Δ x,

(2.8.2)

а в пределе при Δ x→ 0

k’ = δy / δx,

(2.8.3)

что поясняется рис. 2.8.1.

Единица измерения коэффициента преобразования обусловлена единицами измерения величин x и y.

Иногда используют безразмерный относительный коэффициент преобразования η, которым называют отношение относительных приращений выходной и входной величин

η =(Δ y / y)/(Δ x / x)=(Δ y /Δ x)/(y / x)

(2.8.4)

или, при x→ 0,

η’= (dy / dx)/(y / x).

(2.8.5)

Если функция y=F (x) является пропорциональной зависимостью, то k=k’=const, а η=η’= 1.

Применительно к отдельным функциональным элементам коэффициент преобразования называют по-разному. Для датчиков – это чувствительность, для радиоламп – это крутизна характеристики, для усилителей – это коэффициент усиления по току, напряжению или мощности и т. д.

Требования к значению коэффициента преобразования обусловлены назначением элемента. Так, например, применительно к датчикам требуется максимальная чувствительность (желательно чтобы k→max), а к стабилизаторам – минимальная (желательно чтобы k→ 0).

Следует отметить, что многие системы (элементы, звенья) обладают обратной связью. Например, усилители могут обладать обратной связью по току и напряжению.

Для увеличения k используется положительная обратная связь, а для стабилизации k – отрицательная обратная связь.

2. Погрешность – отклонение выходной величины y от истинного её значения вследствие изменения внутренних свойств элемента или внешних условий его работы (рис. 2.8.2).

3. При наличии погрешности фактическая характеристика y _ф =F (x)отлична от градуировочной y _г =F (x). Погрешность может иметь различные названия в зависимости от причин, вызвавших её. Она может быть температурной, частотной, зависеть от колебаний напряжения питания, обусловленной старением элементов и др.

Рис. 2.8.1 Рис. 2.8.2

При характеристике свойств элементов используют понятия абсолютной, относительной и приведенной относительной погрешности.

4. Абсолютная погрешность

Δ y=|y ф –y г |,

(2.8.6)

где y _ф – фактическое значение выходной величины, а y _г – её градуировочное значение.

5. Относительная погрешность выражается в % по

δ= (Δ y/y)×100,

(2.8.7)

а приведенная относительная погрешность – по

δ п = (Δ y/y max)×100,

(2.8.8)

где y _max – максимальное значение выходной величины, определяющее диапазон её изменения.

Обычно для оценки точности элементов используется приведенная относительная погрешность.

5. Порог чувствительности – минимальное по абсолютной величине приращение входной величины Δx, вызывающее изменение выходной величины y. Интервал [ x ₁ ÷x ₂] (рис. 2.8.3) называют зоной нечувствительности.

Причиной существования порога чувствительности является наличие люфтов, трения или гистерезиса у различных исполнительных устройств (двигателей, реле и т. д.), а также наличие дрейфа и шумов на выходе усилителей.

6. Временем регулирования (быстродействием) t _р называют минимальное, с момента подачи ступенчатого воздействия, время, когда отклонение выходной величины от установившегося значения не превышает некоторой заданной величины отклонения (Δ). Обычно принимают Δ=(0,05÷0,1) h(∞), где h (∞) – установившееся значение переходной характеристики. Значение t _р определяется из y=xWe ^-jωt или из y(е)=y _max e ^-jωt.

Для определения t _р проводят параллельно прямой (рис. 2.8.4) h(t)=h(∞) на расстоянии Δ прямые выше и ниже переходной характеристики (прямой h (∞)), тогда время t _р – это время с момента подачи ступенчатого воздействия, когда переходная характеристика в последний раз пересекает любую из двух проведенных прямых на расстоянии Δ.

7. Перерегулирование (в теории автоматического регулирования) определяется по (рис. 2.8.4)

σ= {[ h max– h (∞)]/ h (∞)×100%,

(2.8.9)

где h _max – максимальное значение переходной функции h (∞). Если h (∞)=0, то перерегулирование σ= (h _max/ А ₀)×100 %,здесь А ₀ – ступенчатая реакция на единичное 1(t) воздействие (x₀=1(t)), обычно А ₀=1, а Δ=0,01÷0,1 А₀

Рис. 2.8.3 Рис. 2.8.4

8. Устойчивость. Непрерывная линейная стационарная САУ или САР называется устойчивой, если асимптотически устойчиво какое-либо её невозмущенное (заданное) движение.

Если заданы внешние воздействия, то уравнение линейных стационарных САУ или САР можно представить в виде

(a 0 p ^n+ a 1 p ^n-1+ …+ a n) x (t) =y (t),

(2.8.10)

где a _i(i =0, 1, …, n) – заданные постоянные коэффициенты, p ⁱ – символы дифференцирования указанных (i) порядков, а y (t) – заданная функция реакции во времени.

Общее решение уравнения (13.10) имеет вид

x (t) =x в(t)+ x с(t),

(2.8.11)

где x _в(t) – частное решение неоднородного уравнения (2.8.10), а x _с(t) – общее решение однородного уравнения

(a 0 p ^n +a 1 p ^n-1+ … + a n) x (t)=0.

(2.8.12)

Частное решение x _в(t) определяет вынужденное движение, а общее решение x _с(t) – свободное движение, т. е. движение, которое не зависит от внешних воздействий и определяется только начальными условиями.

Невозмущенное движение задается внешним задающим воздействием и при отсутствии внешних возмущающих воздействий совпадает с вынужденным движением x _в(t), поэтому линейная система устойчива, когда выполняется условие

lim x c(t)=0при t→∞.

(2.8.13)

Это соотношение можно принять за определение устойчивости линейных непрерывных систем и звеньев. Устойчивость линейной системы, т. е. выполнение условия (2.8.13), зависит от её характеристического уравнения

a 0 p ^n +a 1 p ^n-1 + … +a n,

(2.8.14)

левая часть которого называется характеристическим полиномом. Характеристический полином системы, с точностью до постоянного множителя и обозначений переменной, совпадает с её собственным оператором и знаменателем её передаточной функции. Характеристический полином замкнутой системы при отрицательной обратной связи (рис. 2.8.5) равен сумме R (s) +Q(s) числителя R (s) и знаменателя Q (s) передаточной функции W (s) =R (s)/ Q (s) разомкнутой системы.

Рис. 2.8.5 Рис. 2.8.6

Для того чтобы линейная непрерывная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, т. е. требуется выполнение условия

Re x i <0, i= [1, …, n ].

(2.8.15)

На комплексной плоскости (рис. 2.8.6) корни можно представить в виде точек, при этом корни с отрицательной вещественной частью расположатся в левой, разделенной осью ординат, полуплоскости.

Для того чтобы линейная непрерывная система была устойчива, необходимо и достаточно, чтобы все корни её характеристического уравнения были бы левыми, т. е. располагались бы в левой полуплоскости.

В общем случае, если все постоянные коэффициенты характеристического уравнения САУ положительны – система устойчива.

В частном случае, для устойчивости линейных непрерывных систем первого и второго порядков необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были бы одного знака (или все больше нуля, или все меньше нуля). Это обстоятельство, очевидно, позволяет судить об устойчивости указанных систем без вычисления корней их характеристических уравнений.

Качество системы можно рассматривать, только если она устойчива. Неустойчивые системы – неработоспособны.

К корневым показателям качества систем относятся степень устойчивости и колебательности.

6. Степенью устойчивости ζ называется расстояние от мнимой оси (рис. 2.8.6) до ближайшего корня характеристического уравнения, т. е.

ζ=min | Re x i|

(2.8.16)

для всех x _i. Степень устойчивости системы характеризует её быстродействие. При прочих равных условиях, чем больше ζ, тем быстрее затухает переходной процесс.

7. Колебательность определяется (рис. 2.8.6) как

μ=max|Im x i/ Re x i| =|Im max x i/ Reminx i|,

(2.8.17)

где значение μ – мера склонности системы к колебаниям.

СТРУКТУРА СРЕДСТ АВТОМАТИКИ

Общие характеристики

В теории автоматического управления (ТАУ) рассматривают математическую модель системы автоматического управления (САУ), т. е. модель, которая получается в результате её математического описания. Математическое описание может быть аналитическим, графическим и табличным.

Для получения математического описания системы составляют описание ее отдельных элементов. В частности, для получения уравнения САУ составляются уравнения для каждого входящего в нее элемента. Совокупность полученных уравнений и дает аналитическое описание САУ. При получении математического описания исходят из противоречивых требований. С одной стороны, модель должна полнее отражать свойства оригинала, а с другой, быть по возможности простой, чтобы не усложнять исследования. Обычно САУ описываются нелинейными уравнениями.

Для сокращения степени сложности описания нелинейные уравнения стараются линеаризовать, т. е. перейти от исходной нелинейной модели к более простой линейной. Линеаризации бывают обычные, гармонические, статистические и др. Обычными линеаризациями называют те, что основаны на разложении нелинейной функции в ряд Тейлора в окрестности некоторой точки и отбрасывании нелинейных слагаемых.

Математическая модель любой части САУ называется звеном. В частности, звеном может быть математическая модель всей системы или любого её элемента.

Звенья, передаточные функции которых имеют вид элементарных множителей типа

k, s, (s + d 1), (s ^2+ d 1 s + d 2),

(3.1.1)

(где s – оператор преобразования Лапласа), как результат разложения полинома произвольного порядка и элементарных дробей вида

1/ s, 1/ (s + d 1), 1/(s ^2+ d 1 s + d 2)

(3.1.2)

называют элементарными линейными.

Элементарные множители, представляющие собой полиномы первого и второго порядка, можно преобразовать к принятому в теории автоматического управления виду:

k (Ts +1), k (T ^2 s 2±2 ξTs ±1), 0≤ ξ ≤1.

(3.1.3)

При этом k (k >0) называется передаточным коэффициентом; Т (Т >0) – постоянной времени (имеет размерность времени); ξ (0≤ ξ ≤1) – коэффициентом демпфирования.

Уравнение звена, описывающее его переходной процесс, называется уравнением динамики. А уравнение звена, описывающее его поведение при постоянном входном воздействии (x = x ⁰ и при t →∞) и установившемся значении выходной величины, – уравнением статики.

Любое стационарное линейное непрерывное звено с двумя входами описывается уравнением вида

a 0 y ^(n)+ a 1 y ^(n-1)+…+ a n y=b 0 x ^(n)+…+ b n x+c 0 f ^(l)+ c 1 f ^(l-1)+…+ c l f,

(3.1.4)

где y ⁽ⁱ⁾, x ⁽ⁱ⁾, f ⁽ⁱ⁾ – i -е производные по времени.

Линейные САУ (звенья)

К линейным системам относят все системы, которые могут быть описаны линейными дифференциальными уравнениями.

Для линейных систем (звеньев) справедлив принцип суперпозиции: реакция системы на несколько одновременно приложенных воздействий равна сумме реакций системы на каждое воздействие в отдельности

y (t)= y x(t)+ y f(t).

(3.1.5)

Благодаря принципу суперпозиции исследование систем с несколькими входами всегда можно свести к исследованию систем с одним входом:

(a 0 p ^n +a 1 y ^n-1 +…+an) y= (b 0 p ^m +b 1 p ^m-1 …+b m) x.

(3.1.6)

Для описания САУ используются две различные передаточные функции – в операторной форме и в изображениях Лапласа. Для операций дифференцирования введен оператор дифференцирования (p) – py = dy/dt, p ⁱ y/dt. Передаточной функцией в операторной форме W (p) называется отношение собственного оператора (при выходной величине) Q (p) к оператору воздействия (при входной величине) R (p). Передаточной функцией в изображениях Лапласа W (s) (здесь s – переменная преобразования Лапласа) называется отношение изображений Лапласа выходной величины Y (s) к входной величине X (s) при нулевых начальных условиях.

Согласно определению,

W (p) =Q (p)/ R (p)=(b 0 p ^m+ b 1 p ^m-1+…+ b m)/(a 0 p ^n +a 1 p ^n-1 +…+a n

(3.1.7)

и

W(s)=Y(s)/X(s)=(b 0 s ^m +b 1 s ^m-1+…+ b m)/(a 0 s ^n +a 1 s ^n-1 +…+a n,

(3.1.8)

а уравнения звена через W (p) и W(s) имеют вид

y=xW (p)

(3.1.9)

и

Y (s) =yW (s),

(3.1.10)

тогда, очевидно, имеет место формальная подстановка p=s, а W (p) =W (s). Такая связь между двумя формами передаточных функций справедлива только для стационарных систем.

Функция W(jω), которая получается из W (s) при подстановке в неё s= jω

W (jω)=[ a 0(jω)^n+ a 1(jω)^n^–^1+ a n/ b 0(jω)^m+ b 1(jω)^m^–^1+ + b m+ c 0(jω)^i+ c 1(jω)^i^–^1++ c k]

(3.1.11)

называется частотной передаточной функцией. Её можно представить как

W (jω)= U (jω)+ jV (jω)= A (ω)^ejφ^(^ω^),

(3.1.12)

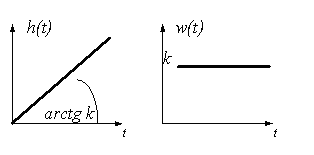
где A (ω)= [ U² (ω)+ V² (ω)], а φ (ω)=arg W (jω).

Если система (звено) имеет q входов и r выходов, то её можно описать qr передаточными функциями.

Переходные и импульсные переходные характеристики называются временными.

Переходной функцией звена называется функция h (t), которая описывает его реакцию (изменение выходной величины) на единичное ступенчатое воздействие 1(t) при нулевых начальных условиях

1(t)=0, при t <0, и 1(t)=1, при t ≥0,

(3.1.13)

а график переходной функции – кривая зависимости h (t) называется переходной или разгонной характеристикой.

Импульсной переходной, или весовой, функцией называется функция w (t), которая описывает реакцию звена на единичное импульсное воздействие при нулевых начальных условиях, а график импульсной переходной функции называют импульсной переходной характеристикой.

Единичный импульс – импульс с единичной площадью бесконечно малой длительности, он описывается дельта-функцией – δ (t).

В соответствии с определением w (t), при x (t)= δ (t) y (t)= w (t), а т. к. L { δ (t)}=1, то при x ’= δ (t) L { w (t)}= W (s), тогда звено – это преобразователь входной величины x = δ (t) в выходную y = w (t) или – x =1(t) в y = h (t).

К линейным звеньям относятся:

- пропорциональное звено с функциями

W (s) =k, W (jω) =k, U (ω) =k, V (ω)=0, A (ω) =k, φ (ω)=0

(3.1.14)

и характеристиками (рис. 3.1.1), первого порядка инерционности

- дифференцирующее звено с функциями

W (s) =ks, W (j ω) =jkω, U (ω)=0, V (ω) =kω, A (ω) =kω, φ (ω) =π/2, h (t) =kδ (t), w (t) =kδ’ (t)

(3.1.15)

и характеристиками (рис. 3.1.2) первого порядка инерционности;

Рис. 3.1.1 Рис. 3.1.2

- интегрирующее звено с функциями

W (s) =k/s, W (jω) =–jkω, U (ω)=0, V (ω) =–kω, A (ω) =k/ω, φ (ω) =–π/ 2, h (t) =kt, w (t) =k

(3.1.16)

и характеристиками (рис. 3.1.3), первого порядка инерционности;

Рис. 3.1.3

- форсирующее звено с функциями

W (s) =k/ (Ts+ 1), W (jω) =j (Tω +1), U (ω) =k, V (ω) =kTω, A (ω) =k√ ((Tω)^2 + 1), φ (ω) =arctg (Tω), h(t) =k [ Tδ (t) + 1(t)], w (t) =k [ Tδ’ (t) +δ (t)];

(3.1.17)

- апериодическое звено с функциями

W (s) =k/ (Ts +1), W (jω) =k/ (Tjω +1), U (ω) =k/ [(Tω)^2+1], V (ω) =kTω /[(Tω)^2+1], A (ω) =k/[√ (Tω)^2 + 1)], φ (ω) =arctg (Tω), h (t) =k (1 –e ^–^t/T), w (t) = (k/T) e ^–^t/T

(3.1.18)

и характеристиками (см. рис. 3.1.4) первого порядка инерционности;

Рис. 3.1.4

- колебательное звено (при 0<ξ<1 см. рис. 3.1.5) с функциями

W (s) =k /(T^2s^2+2ξTs+ 1), W (jω) =k /{[1–(Tω)^2]^2 +j 2 ξTω)}, U (ω) =k /[1– (Tω)^2]/[1– (Tω)^2]^2+(2 ξTω)^2], V (ω) = 2 k ξ Tω /[1– (Tω)^2]^2+(2ξ Tω)^2, A (ω) =k /(√[1– (Tω)^2]^2+(2ξ Tω)^2, φ (ω)= – arctg [2ξ Tω /[1– (Tω)^2]} при ω≤ 1/ T и φ (ω)= – πarctg {2ξ Tω /[1– (Tω)^2]}при ω >1/ T h (t) =h (t) =k {1–[√(α ^2+ β ^2)]/ e^-^α^tsin (βt+φ 0)}, w (t) = [ k (α ^2+ β ^2) e^-t/Tsin βt,

(3.1.19)

где α= ξ/ T, β= [√(1–ξ²)]/T, φ ₀ =frctg [√(1–ξ²)]/ ξ, при ξ =0 звено называется консервативным с характеристиками (рис. 3.1.6) первого порядка инерционности.

Рис. 3.1.5 Рис. 3.1.6

Нелинейные САУ (звенья)

К нелинейным системам относят все системы, которые не могут быть описаны линейными дифференциальными уравнениями.

Множество нелинейных систем настолько велико, что практически нельзя говорить о едином классе нелинейных систем, противостоящих классу линейных систем.

Нелинейную систему можно представить в виде соединения двух блоков: линейной части (ЛЧ), описываемой обыкновенными дифференциальными уравнениями с постоянными коэффициентами, и нелинейного элемента (НЭ), например рис. 3.1.7.

Рис. 3.1.7

Нелинейный элемент при этом считается безынерционным звеном, т. е. нелинейность рассматриваемого класса систем обусловлена статической характеристикой одного из её элементов.

Типовые нелинейные характеристики:

- ограничение (насыщение) (рис. 3.1.8), для которой y=b при x>a, y= (b / a) x при │ x │≤ a; y=-b при x<-a;

- зона нечувствительности (рис. 3.1.9), для которой y=k (x+a)при x <- a, y= 0при │ x │ ≤a; y=k (x-a) при x>a;

Рис. 3.1.8 Рис. 3.1.9

- зона нечувствительности с ограничением (рис. 3.1.10), для которой y =- b при x <- a ²; y=k (x+a ₁)при – a ₂< x<-a ₁; y= 0при │x│> a; y= (x-a ₁) – при a ₁ ..x a ₂;

- реле (рис. 3.1.11), для которой y=-b при x< 0; y=b при x> 0;

Рис. 3.1.10 Рис. 3.1.11

- реле с зоной нечувствительности (рис. 3.1.12), для которой y=-b при x <- a, y= 0 при │ x │≤ a; y=b при x>a;

- кубическая парабола (см. рис. 3.1.13), для которой y=lx ³- b;

Рис. 3.1.12 Рис. 3.1.13

- люфт (рис. 3.1.14), для которой y=k(x-a) при x> 0и y=k(x+a) при x< 0

- реле с гистерезисом (рис. 3.1.15), для которой y=b при x> 0и x> 0; y=–b при x<a и x<a и x> 0 и y=b при x>–a и x< 0; y=–b при x<–a и x< 0

- реле с гистерезисом и зоной нечувствительности (рис. 3.1.16.)

Рис. 3.1.14 Рис. 3.1.15 Рис. 3.1.16

3.2. Структурные схемы САУ и правила их преобразования

Структурной схемой называется графическое представление математической модели системы в виде соединений звеньев.

К обычным линейным динамическим звеньям относятся: усилительное (безынерционное, пропорциональное), интегрирующее, устойчивое колебательное (при ξ ≈1 – апериодическое и при ξ =0 – консервативное), дифференцирующее первого порядка, дифференцирующее второго порядка.

К особым элементарным звеньям линейных САУ относят: неминимальнофазовые, неустойчивые, с распределёнными параметрами, иррациональные, трансцендентные.

Структурно звенья изображаются условными символами (рис. 3.2.1), чаще всего в виде прямоугольников с указанием входных и выходных величин, а также передаточной функции или уравнения этого звена.

Рис. 3.2.1

Исключение составляет суммирующее звено, которое чаще изображают в виде круга, для наглядности разделенного на секторы, как показано на рис. 3.2.2.

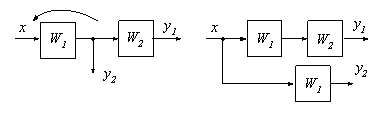
Рис. 3.2.2

Для обозначения обратной (отрицательной) величины сектор затемняют или ставят знак «–».

Основные выражения для преобразования структурных схем определяются при известных передаточных функциях в операторной форме [ K ₁(p), K ₂(p), …, K _n(p)] (p – оператор дифференцирования) или в преобразованиях Лапласа [ W ₁(s), W ₂(s), …, W _N(s)] (s – оператор преобразования Лапласа) и представляют собой передаточные функции звеньев.

Основные типы соединений звеньев – это последовательное, параллельное и обратное.

Последовательное соединение (рис. 3.2.3) – это соединение, при котором выходная величина предшествующего звена является входным воздействием последующего звена

При преобразовании структурных схем цепочку из последовательно соединенных звеньев можно заменить одним звеном с передаточной функцией, равной произведению передаточных функций отдельных звеньев

W =Π W i по всем i =[1, …, n ].

(3.2.1)

Рис. 3.2.3

Параллельное соединение – это соединение, при котором на входы всех звеньев подается одно и то же воздействие, а выходные величины суммируются.

Цепь из параллельно соединенных звеньев (рис. 3.2.4) можно заменить одним звеном с передаточной функцией, равной сумме передаточных функций входящих в неё звеньев

W =Σ W i по всем i =[1, …, n ].

(3.2.2)

Обратное соединение (рис. 3.2.5) – это соединение, при котором звено охвачено обратной связью. При этом выходной сигнал одного звена через какое-либо другое звено подается на вход первого.

Рис. 3.2.4 Рис. 3.2.5

Такое соединение называют соединением обратной связи. Участок цепи от точки приложения входного воздействия х до точки съема выходного сигнала у (в направлении распространения сигнала) называют прямой цепью, а участок от точки съёма выходного сигнала до сумматора называют обратной связью.

Если сигнал обратной связи х ₁ вычитается из входного воздействия х, то обратная связь называется отрицательной (ε = х - х ₁), в противном случае – обратная связь называется положительной (ε = х + х ₁).

Если передаточная функция W _ос=1, то обратная связь называется единичной, а схему структурно изображают, как показано на рис. 3.2.6.

Рис. 3.2.6

Звено, охваченное обратной связью, можно заменить одним звеном с передаточной функцией

W = W п/(1± W п W ос),

(3.2.3)

где знак «+» в знаменателе правой части берётся при отрицательной обратной связи, а знак «-» - при положительной обратной связи. Это объясняется тем, что петлевое преобразование W _п W _ос может быть действительным числом W _п W _ос>0, тогда положительная связь, а если W _п W _ос>0, но действительное число, то обратная связь является отрицательной.

Величина (1± W _п W _ос) – глубина обратной связи. При размыкании замкнутой цепи сразу после сумматора получается цепь из двух последовательно соединенных звеньев, её передаточная функция, равная W _р= W _п W _ос, называется передаточной функцией разомкнутой цепи (системы), она и определяет петлевое преобразование.

Перенос сумматора. При переносе сумматора через звено по ходу распространения сигнала добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор, что поясняется рис. 3.2.7.

Рис. 3.2.7

При переносе сумматора через звено против хода сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор (рис. 3.2.8).

Рис. 3.2.8

При переносе сумматора возникают неэквивалентные участки цепи (обозначено жирными линиями). Поэтому при преобразовании структурных схем нельзя переносить сумматор через точку съёма сигнала (без специальных мер преобразования).

Перенос узла. При переносе узла через звено по ходу сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел (рис. 3.2.9).

Рис. 3.2.9

При переносе узла через звено против хода сигнала добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел (рис. 3.2.10).

Рис. 3.2.10

Перестановка узлов (рис. 3.2.11) и сумматоров (рис. 3.2.12) допустима, но при перестановке сумматоров участки (выделено жирным) между сумматорами не являются эквивалентными.

Рис. 3.2.11

Рис. 3.2.12

Вычисление передаточной функции одноконтурной системы. Замкнутая система называется одноконтурной, если при её размыкании (сразу после сумматора) получается цепочка из последовательно соединенных звеньев, или цепь, не содержащая параллельных соединений и обратных связей (рис. 3.2.13.).

Рис. 3.2.13

Используя правила преобразования при последовательном и обратном соединениях, получают следующее правило: передаточная функция W _yx одноконтурной системы относительно входа х и выхода у равна передаточной функции прямой цепи W _п, деленной на (1+ W _р) при отрицательной и – на (1- W _р) при положительной обратной связи:

W yx= W п/(1± W p),

(3.2.4)

где W _p= W _п W _ос – передаточная функция разомкнутой цепи.

Вычисление передаточной функции многоконтурной системы. Замкнутая система называется многоконтурной, если при её размыкании получается цепь, содержащая параллельные или обратные связи; или замкнутая система называется многоконтурной, если она кроме главной обратной связи содержит параллельные или местные обратные связи.

Многоконтурная система не имеет перекрещивающихся связей, если любые два контура, образованные параллельными или обратными связями, не имеют общих участков (рис. 3.2.14), или если один контур вложен внутрь другого (рис. 3.2.15).

Рис. 3.2.14

Рис. 3.2.15

Многоконтурная система имеет перекрещивающиеся связи, если какие-либо два контура, образованные параллельными или обратными связями, имеют общий участок (на рис. 3.2.16 выделен жирными линиями).

При вычислении передаточных функций нужно, прежде всего, освободиться от перекрещивающихся связей путем переноса и перестановки сумматоров и узлов. Затем, используя правила преобразования параллельного и обратного соединений, преобразовать многоконтурную систему в одноконтурную.

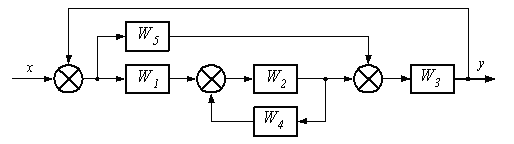
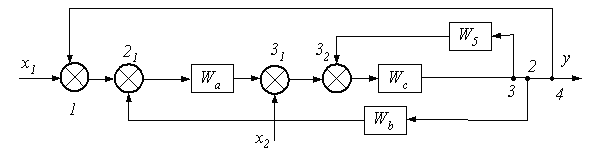
Рис. 3.2.16

Пример. Определить y системы на воздействия x ₁ и x ₂.

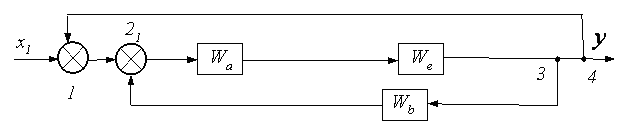
Алгоритм решения задачи выполняется в последовательности:

а) сумматор 2 представить в виде двух сумматоров 2₁ и 2₂, узел 2 перенести через звено W ₃ по ходу сигналов x₁ и x₂, а узлы 3 и 4 расположить на одной прямой узлов и сумматоров;

б) контур звена W₁ и сумматор 2₂ заменить одним звеном с W_a=W₁/(1–W₁), цепочку из звеньев W₄ и 1/W₃ заменить одним звеном c W_b=W₄/W₃, цепочку из звеньев W₂ и W₃ заменить одним звеном c W_c=W₂W₃ сумматор 3 представить в виде сумматоров 3₁ и 3₂;

в) контур из сумматора 3₂, звена W_C, узла 3 и звена W₅ заменить одним звеном с W_e=W_c/(W_c–W_cW₅);

г) преобразовать схему для анализа по входу x₁ и входу x₂, соответственно

или, для наглядности, в таком виде

д) по входам x₁ и x₂ – цепочку W_aW_e=W_k, а вложенный контур из W_a, W_e, узла 3 и сумматора 2₁ заменить на звено с W_m=W_aW_e/(1–W_aW_eW_b), а контур из W_m, узла 4 и сумматора 3₁ заменить звеном W_v, тогда y_x1=x₁W_v, а y_x2=x₂W_v/W_a, а, с учетом принципа суперпозиции, y=x₁W_v+x₂W_v/W_a.

3.3. Автоматическое регулирование

Простейшей системой автоматического управления (САУ) технологическим оборудованием (ТО) является система автоматического регулирования (САР).

Структурная схема САР (рис. 3.3.1) включает объект регулирования (ОР), вычислительное звено – вычислитель или регулятор (ВР), устройство сравнения (УС – сумматор), датчик (Д), задатчик (З), регулирующий орган (РО) на рис. 18.1 совмещен с исполнительным механизмом (ИМ), объединенным потоками материального и информационного характера.

В САР задатчиком называется устройство, посредством которого настраивается автоматический регулятор (АР) на заданное значение регулируемой величины, а датчиком – чувствительный элемент, реагирующий на состояние регулируемой величины. Исполнительный механизм (ИМ) с регулирующим органом (РО) – устройство, непосредственно изменяющее количество вещества или энергии, поступающих в ОР при регулировании. ИМ – это позиционер, позиционное реле, усилитель с устройством жесткой обратной связи или сервомотор – механизм, управляющий перемещением ИМ под воздействием управляющего устройства АР, а РО – это задвижка, вентиль или др. ограничитель материального потока.

Рис. 3.3.1