
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование возмущенного движения транспортного средстваСодержание книги
Поиск на нашем сайте
Основным результатом оценки динамических и точностных характеристик системы автоматического управления (СУ) транспортным средством (ТС), например самолетом (ЛА), являются натурные эксперименты (испытания). Однако в целях предварительной оценки должны быть привлечены результаты математического и стендового моделирования. Использование результатов моделирования контура «СУ-ТС» является обоснованным, если продемонстрирована их сходимость с результатами натурного эксперимента. При оценке адекватности математической модели ЛА выделяют, по крайней мере, два аспекта – детерминированный и статистический. Первый из них предполагает оценку сходимости результатов моделирования и испытаний по критерию динамического подобия, которое устанавливается путем сравнения динамических характеристик ЛА, полученных в результате расчета и эксперимента в условиях детерминированных возмущений повышенной интенсивности. Уравнения движения ЛА с СУ составляются по результатам аэродинамических продувок, контролируемых аппаратными средствами с резервированием их функциональных возможностей. При этом проверке подвергается математическая модель, которая затем используется в процессе статистического моделирования для уточнения характеристик СУ. При этом полный диапазон возможных изменений контролируемых параметров движения ЛА делится на две области: больших (Δ h >±4÷5 σ) и малых (Δ h <±2÷3 σ) ошибок управления. Действие на ЛА возмущения чаще всего является нормальным случайным процессом; динамическая система «ЛА–СУ» в малом диапазоне изменения её переменных квазилинейна и обладает свойством нормализовать проходящие через неё сигналы, что позволяет в диапазоне Δ h <±2÷3 σ распределение ошибок управления считать нормальным. Статистическое моделирование проводится с учетом имеющих место в натурных экспериментах случайных факторов (веса, центровки, ветра и т. д.) как в части диапазона их изменения, так и частоты варьирования различных уровней. Натурные (лётные) испытания статистически независимы и охватывают ожидаемые условия будущей эксплуатации ЛА. Предполагается, что математическая модель и реальный ЛА статистически подобны, если расчетные и опытные выборки извлечены из одной и той же генеральной нормально распределенной совокупности. Традиционные критерии статистического подобия двух выборок, извлеченных из нормально распределенной генеральной совокупности, основаны на сравнении дисперсии и математического ожидания. Дисперсии признаются равными, если выполняется правило (критерий Фишера)
где выборочные оценки дисперсии параметров соответственно определимы из выражений
где x i – значение исследуемого параметра в i -м эксперименте (расчетно или экспериментально полученное);
n 1, n 2 – объемы выборок; F (1– a )(n 1–1, n 2–1) – квантиль распределения Фишера с (n 1–1, n 2–1) степенями свободы уровня (1– α); α – уровень значимости. Для сравнения математических ожиданий используется одно из следующих решающих правил:
где
T (1– a /2)(n 1+ n 2–2) – квантиль распределения Стьюдента с числом степеней свободы уровня (1– a /2)=(n 1+ n 2–2): при принятии гипотезы неравенства дисперсии
где число степеней свободы V определяется в соответствии с правилом Сэттервейта:
и в зависимости от конкретных значений S 12 и S22 меняется в диапазоне min { n 1, n 2}≤=(n 1+ n 2–2). Применение решающих правил (4.2.1) и (4.2.2) в случае статистической неоднородности сравниваемых выборок позволяет выявить источник неоднородности – систематические и/или случайные ошибки. Однако выше описанные критерии имеют два существенных недостатка: - для принятия решения необходимо наличие серии натурных экспериментов, и в случае проведения доработок требуется повторение всего объёма натурных экспериментов; - раздельное сравнение дисперсии и математических ожиданий приводит к снижению достоверности принимаемых решений, так как (1– а)=(1– а 1)(1– а 2), где а 1 и а 2 – уровни значимости при проверке равенства дисперсии и равенства математических ожиданий. Приведенные ниже критерии проверки однородности результатов моделирования натурных экспериментов лишены указанных недостатков. Решение о статистической однородности результатов моделирования и натурных экспериментов может быть принято после проведения каждого натурного эксперимента с использованием следующего критерия отбраковки аномальных значений параметров:
где оценки Проблема множественного сравнения может быть решена переходом на сравнение толерантных интервалов. Следует отметить, что при построении толерантного интервала по результатам выборки (x 1÷ x n) объёма n из генеральной совокупности, имеющей нормальное распределение N (m, σ 2), определяют его границы, являющиеся реализациями функций выборок X н, X в, относительно которых справедливо утверждение: внутри толерантного интервала с доверительной вероятностью γ заключается не менее чем доля R всей совокупности, т. е. P { X н≤ x ≤ X в}≥ R = γ или P { где f (x) – плотность распределения вероятности параметра x. Оценка толерантного множителя z, значения которого табулированы для различных значений n, R и γ, причем, z ≈(x– M | z |= U r и дисперсией D | z |=1/ n + z 2/2(n –1), где U r – квантиль стандартного нормального распределения. Таким образом, задача сравнения статистической однородности двух выборок сводится к сравнению двух математических ожиданий при неравных дисперсиях. Соответствующее решающее правило имеет вид
Достоверность принимаемых решений характеризуется вероятностями ошибок первого α и второго β рода (вероятностями ошибочных приемки и отбраковки, соответственно). Для определения значения β необходимо задать альтернативные гипотезы. При проверке равенства дисперсий альтернативную гипотезу удобно представлять в виде σ 1= kσ 2. Тогда зависимость между α, β, k и n определяется из граничных соотношений S 12/ S 2= F (1– α )(n 1–1, n 2–1); S12/ kS 22= F β(n 1–1, n 2–1), откуда «расстояние» между нулевой и альтернативной гипотезами определимо из выражения k = F (1– α)(n 1–1, n 2–1) /F β(n 1–1, n 2–1). Таким образом, при принятии гипотезы равенства дисперсий с вероятностью β, эти дисперсии могут различаться в k раз. При проверке равенства математических ожиданий альтернативную гипотезу удобно задавать в виде m 1= m 2+Δ. Тогда при альтернативной гипотезе статистика равна | с параметром нецентральности (Δ/ σ)[(n 1+ n 2)/ n 1 n 2]1/2. Нецентральное распределение уже при n ≥5 удовлетворительно аппроксимируется нормальным распределением, т. е. P { | =1– Ф { t (1– a /2)(Δ/ σ)[(n 1+ n 2)/ n 1 n 2]1/2[1+0,5 t (1– a /2)2/(n 1+ n 2–2)]–1/2}=1– β, где Ф – интегральная функция стандартного нормального распределения. Следовательно, U β= t (1– a /2)(Δ/ σ)[(n 1+ n 2)/ n 1 n 2]1/2[1+0,5 t (1– a /2)2/(n 1+ n 2–2)]–1/2. При использовании решающего правила (36.4) альтернативная гипотеза задается в виде U R1= U R2+Δ U R. Тогда зависимость между a, β, n и Δ U R1 определяется из граничных условий | z 1–z2|(D 1+ D 2)–1/2= U (1–a/2) и | z 1–z2+Δ U R|(D 1+ D 2)–1/2, и, следовательно, Δ U R|(D 1+ D 2)–1/2= U (1–a/2)– U β. Таким образом, описанный выше метод сравнения толерантных множителей для проверки адекватности математической модели возмущенного движения ЛА имеет существенное преимущество перед традиционными методами. При принятии гипотезы статистической однородности результатов моделирования и натурного эксперимента требования к точностным характеристикам параметров считаются подтвержденными.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

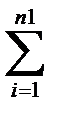 (x i–
(x i–  1)2; S 22=(n 2–1)–1
1)2; S 22=(n 2–1)–1  f (x) dx н≤ x ≤ X в}≥ R = γ,
f (x) dx н≤ x ≤ X в}≥ R = γ,


