
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поскольку координатами вектора является градиентСодержание книги
Поиск на нашем сайте
в котором коэффициенты при линейных членах уравнения регрессии b 1, b 2, … b k не допустимо определять по результатам нескольких пробных экспериментов в окрестности исходной точки. В этом случае приращение целевой функции y, соответствующее приращению xi, можно считать пропорциональным значению производной
После нахождения составляющих градиента выполняется рабочий шаг по направлению к экстремуму (см. рис. 1.4.3.):
где р ш – параметр рабочего шага, который выбирают в зависимости от его номера h на расстоянии от оптимума γ: p н= p/ (h,γ); p=const, h – номер шага; 0< γ <0,5, оптимально (γ =0,25).
Рис. 1.4.3 Показателем выхода в область оптимума является малое значение модуля градиента (grad y (x)→0), т. е. все коэффициенты b i становятся незначимыми или равными 0. В градиентном методе важен выбор шага, т. к. при слишком малом шаге необходимо большое число экспериментов, а если шаг велик, то можно «проскочить» экстремум. Этот метод объединяет характерные элементы методов Гаусса-Зейгеля и градиента. Так, шаговое движение при этом методе осуществляется в направлении наибольшего изменения целевой функции (в направлении роста градиента), но в отличие от метода градиента корректировка направления движения проводится не после каждого шага, а после достижения частного экстремума целевой функции, как при методе Гаусса-Зейгеля. Метод крутого восхождения (Бокса - Уилсона) Практически поиск оптимума методом крутого восхождения выполняется следующим образом: 1) Вблизи исходной точки x 0 проводится эксперимент для определения grad y (x 0), результаты эксперимента подвергаются статистическому анализу, определяются коэффициенты bi уравнения регрессии. 2) Вычисляется произведение b i ∆x i, где ∆x i – шаг варьирования параметра xi при исследовании поверхности отклика в окрестности исходной точки. Фактор, для которого произведение будет максимальным, принимается за базовый δ δ ∆x i. 3) Для базового фактора выбирается шаг движения λδ по направлению к оптимуму, после этого вычисляются размеры шагов при крутом восхождении по остальным переменным процессам. При движении к оптимуму по градиенту все исследуемые параметры должны изменяться пропорционально коэффициентам наклона поверхности отклика b i:
4) Проводятся «мысленные» опыты, которые заключаются в вычислении
значений целевой функции в точках факторного пространства, лежащих на пути к экстремуму, при этом i -я координата (n +1)-й точки определяется
где h =1,..., m, i =1,..., k, λ i= b i ∆x i= b i + (∆x i)/ n. Прогнозируемое значение выходного параметра определяется из формулы
5) Поскольку каждый цикл крутого восхождения приближает к поверхности отклика с большей крутизной, рекомендуется для каждой последующей серии опытов выбирать шаг меньший, чем в предыдущей. 6) Эксперимент прекращается, когда все или почти все коэффициенты b i уравнения (1.4.5) становятся незначимыми или равными нулю, что говорит о выходе в область экстремума целевой функции. Пример: При помощи крутого восхождения для оптимизации математической модели процесса ультразвуковой сварки проволочных выводов ИМС в виде y=9,81+1,42x1+1,27x2+2,21x3 определяем шаг варьирования: Δt=0,1 Δxi, шаг движения xi=bi∆I, тогда x1=0,005∙1,42=0,007, x2=0,005∙1,27=0,006, x3=0,5∙2,21=1,105, находится значение факторов x в начале опыта: x1’=x1ном+∆x1b1=0,15+(0,005∙1,42)=0,157; x2’=x2ном+∆x2b2=0,15+(0,005∙1,27)=0,156; x3’=x3ном+∆x3b3=10+(0, 5∙2,21)=11,1. Начинают крутое восхождение в сторону увеличения переменных x1, x2, x3, которые выбираются на уровне «1». Проводятся «мысленные» опыты, результаты которых заносятся в таблицу (табл. 1.4.1). Наибольшее усилие отрыва Р=14,00 сН в 4-м опыте. Оно подтверждается экспериментальными данными. В пятом опыте yэ не подтверждается yр, поэтому «восхождение» прекращают. Далее переходят к исследованию функции в стационарной области. Шаговое движение к экстремуму продолжают до тех пор, пока не будет достигнута «почти стационарная» область, которая не может быть описана линейным выражением. Таблица 1.4.1
Здесь сильнее проявляется взаимодействие факторов, характеризуемых коэффициентами при квадратных членах полинома (1.4.8), поэтому данную область удается описать с достаточной точностью с помощью полинома второго порядка вида
Для вычисления полинома второго порядка уровней должно быть как минимум на единицу больше степени полинома. Однако полный факторный эксперимент (ПФЭ) типа 3 k нерационален вследствие резкого роста числа экспериментов. Сократить их число можно, используя так называемые центральные композиционные планы (ЦКП). Их особенностью является добавление нескольких специально спланированных экспериментальных точек к матрице ПФЭ для получения плана второго порядка. При k факторах общее число опытов ЦКП
где 2 k – звездные точки, а m0 – число опытов в центре плана. Т. о., к линейной модели добавляются так называемые «звездные точки» с координатами (0, α), лежащими на сфере диаметром 2 α (рис. 1.4.4), и опыты начинают в центре плана. Бокс и Уилсон предложили выбирать плечо α и количество центральных точек (m 0=1) так, чтобы план второго порядка оставался ортогональным (ЦКОП). При k =3 он содержит всего 15 опытов, тогда как при ПФЭ 33=27.
Рис. 1.4.4 В силу ортогональности плана все коэффициенты определяются независимо друг от друга по следующей системе:
В отличие от линейного полинома при ортогональном планировании второго порядка оценки коэффициентов полинома находятся с неодинаковыми дисперсиями σ 2{ b i} =σ 2{ b ij} по системе уравнений (1.4.10). А дисперсия при квадратичных членах уравнения регрессии рассчитывается по формуле
Так же, как и при синтезе линейной модели, обработка результатов при реализации ЦКОП предполагает статистические проверки гипотез воспроизводимости результатов экспериментов, значимости коэффициентов и адекватности моделей. Полученная модель второго порядка используется для нахождения оптимальных технологических режимов. Для двух независимых переменных уравнение в канонической форме имеет вид
Поверхность отклика в зависимости от вида уравнения может быть трех видов: – если коэффициенты В 11 и В 22 имеют одинаковые знаки, то поверхность отклика – эллиптический параболоид, центр которого – искомый экстремум; – при разных знаках В 11 и В 22 поверхность отклика относится к типу минимакса, или «седла». Для нахождения оптимальных технологических режимов целесообразно двигаться по благоприятному крылу «седла». Если один из коэффициентов равен нулю, то поверхность отклика имеет форму нарастающего возвышения (рис. 1.4.5).
Рис. 1.4.5 Для отыскания оптимума следует двигаться по гребню, пока это допускает возможности технологического процесса. Так (см. пример), уместно оценить оптимальные значения всех факторов, в т. ч. Х 2(t, ْ C) и X 3(F, cH). 1.5. Технология производства интегральных схем Укрупненную схему технологического процесса производства интегральных схем (ИС) эпитаксиально-планарной структуры на базе транзисторов n-p-n -типа со скрытым n+ слоем (не считая выращивания и раскроя слитка кремния на пластины, их шлифовку и полировку) можно представить с помощью таких технологических операций: 1. Окисление пластин кремния p -типа; 2. Первая литография на SiO 2; 3. Диффузия n+ - примеси; 4. Снятие окисла, эпитаксия n -слоя; 5. Окисление; 6. Вторая литография на SiO 2; 7. Разделительная диффузия p -примеси; 8. Окисление; 9. Третья литография на SiO 2; 10. Базовая диффузия p -примеси; 11. Окисление 12. 4-я литография на SiO 2; 13. Эмиттерная диффузия n -типа; 14. Окисление; 15. 5-я литография на SiO 2; 16. Металлизация; 17. 5-ая литография (на металле); 18. Вытравливание контактов; 19. Зондовый контроль ИС на пластине; 20. Скрайбирование, ломка пластины, отбраковка; 21. Монтаж кристалла в корпус; 22. Монтаж выводов; 23. Герметизация; 24. Контроль функциональных параметров, отбраковка; 25. Испытания ИС. 1÷20 операции – это групповая обработка. 21÷25 операции – индивидуальная обработка. Отдельные этапы процесса – фотолитография, диффузия, контроль и испытания состоят из 3÷10 операций. Общее число операций изготовления монолитных ИС (без учета заготовительного этапа получения пластин) свыше 100. Продолжительность полного цикла обработки около 100 часов. Цикл групповых процессов обработки ИС заканчивается получением межсоединений – металлических проводников на поверхности кристалла. Контроль параметров отдельных элементов на предшествующих этапах производства чрезвычайно сложен и экономически не выгоден. Целесообразнее сохранять дефектные кристаллы в пластине до конца групповой обработки, а отбраковку выполнять после выполнения межсоединений путем комплексной проверки ИС на функционирование (на работоспособность). Однако специальный анализ брака ИС на отдельных этапах представляет большой интерес с точки зрения выявления узких мест производства (табл. 1.5.1). Для этого используют кристаллы-свидетели. Таблица 1.5.1
В нижеприведенной таблице 1.5.2 (построенной с помощью кристаллов-свидетелей) результат анализа распределения брака выявил, что на индивидуальную обработку поступает лишь около половины кристаллов. Окончательный процент выхода годных ИС свидетельствует о том, что в производство следует запускать в 4 раза больше схем, чем это требуется по плану. Точность выходных характеристик ИС непосредственно зависит от точности электрофизических параметров диффузионных областей. Поэтому важным является межоперационный контроль в процессе диффузии (обычно с помощью пластин-свидетелей). Типичные для эпитаксиально-планарных ИС параметры и допуски приведены в табл. 1.5.2. Процесс производства ИС должен обладать высокой эффективностью, под которой следует понимать высокое качество (высокий процент выхода годных ИС) и низкую трудоемкость. Для обеспечения высокой эффективности производства необходимо соблюдение ряда принципов. Важнейшим является принцип технологической совместимости элементов ИС с наиболее сложным элементом, обычно транзистором. Структура элементов (диодов, резисторов, конденсаторов) должна содержать только те области, на основе которых построен транзистор. Таблица 1.5.2
Поэтому технологическое проектирование изготовления кристалла ИС строится с учетом лишь структуры транзистора, а остальные элементы формируются попутно. Примером нарушения этого принципа является использование МДП конденсатора в ИС с биполярными транзисторами, т. к. такой транзистор требует ряда дополнительных операций, связанных с получением диэлектрика расчетной толщины. В то же время МДП транзистор технологически совмещается с униполярным транзистором в МДП ИС. В биполярных структурах в качестве конденсатора может быть использован обратно смещенный p-n -переход. Т. о., характер и последовательность операций обработки кристалла должны полностью определяться структурой транзистора. Вторым принципом является принцип групповой обработки, которая должна охватывать как можно большее число операций. Возможность групповой обработки ИС обусловлена широким использованием физико-химических процессов (эпитаксия, диффузия, обезжиривание, травление, отмывка), в которых в качестве рабочей среды используют газовые и жидкие вещества. Возможность одновременной обработки больших поверхностей позволяет также вести многоместную обработку нескольких групповых заготовок одновременно на ряде операций. В результате одновременной обработки и получения нескольких тысяч ИС повышается воспроизводимость их характеристик и значительно снижается трудоемкость изготовления отдельных ИС. Так, на пластине диаметром 50 мм можно, например, изготовить 625 ИС размером 1×1 мм или 400 – с размером 1,25×1,25 мм, или 275 – размером 1,5×1,5 мм. Использование пластин большого диаметра лимитируется технологическими трудностями обеспечения равномерных свойств материала на большой площади. Индивидуальные операции на отдельных кристаллах значительно повышают трудоемкость изготовления ИС и снижают экономичность процесса в целом. Важным принципом технологии ИС является принцип универсальностипроцессов обработки, заключающийся в том, что для производства различных по своим функциям ИС применяют идентичные по физической сущности процессы с одинаковыми технологическими режимами. Единая базовая структура для схем различных типов порождает и единую базовую топологию, позволяющую одновременно производить микросхемы различных типов. Третий принцип – это принцип унификации пластин-заготовок, содержащих максимальное число признаков микросхемы. Весь процесс производства ИС можно разделить на 2 этапа: заготовительный этап, в результате которого получают универсальную пластину-заготовку, и этап специальной (избирательной) обработки, в результате которой микросхема приобретает определенные функциональные свойства. Развитие этого принципа предполагает использование так называемого базового кристалла (платины), представляющего собой заготовку, в которой сформирован универсальный набор элементов (с избыточностью). Специальная обработка заключается в получении определенного рисунка межсоединений в соответствии с функциональными свойствами микросхемы данного типа. Высокая чистота технологических сред, в которых осуществляется обработка, является общим требованием радиоэлектронного производства. В производстве же ИС это требование приобретает принципиальное значение, перерастая в принцип высокой чистоты производства в целом. Этот принцип предполагает использование материалов, практически не содержащих посторонних примесей, причем количество сознательно вводимых примесей должно быть строго регламентировано. Требования к чистоте газов, используемых в процессах эпитаксии, диффузии и пассивации, сведены в табл. 1.5.3. Таблица 1.5.3
Содержание пылевых частиц не более 2÷3 в 1 л. газа при размере частиц не более 0,7 мкм. Столь жесткие требования обусловлены очень высокой чувствительностью монокристаллического кремния к инородным атомам или ионам, наличие которых влияет на его свойства и обуславливает неисправный брак ИС. Чем выше степень интеграции (чем больше элементов содержит ИС), тем «чувствительней» она к качеству выполнения операций, тем ниже процент выхода годный ИС. В связи с этим большое значение приобретают операции отмывки пластин, т. е. полного удаления следов реактивов, остающихся от предыдущей обработки. Применяемая при этом вода (сверхчистая) не должна оставлять на поверхности ионы растворенных в ней загрязнений, для чего воду подвергают процессам деионизации (обессоливания). Изложенное требование целиком относится к заготовительному циклу обработки – очистке исходного материала, легированию и выращиванию монокристалла, резке слитка, шлифовке, полировке и пассивации пластин. Так, из-за недостаточно тщательной очистка поверхности перед пассивацией (окислением) кремния образуются дефекты в окисной пленке (поры, включения и т. п.), что приводит к браку в процессе фотолитографии и диффузии. Высокая плотность дефектов в окисной пленке и в исходном кремнии затрудняет внедрение в производство БИС, в которых используются кристаллы большей площади, чем в обычных ИС. Недостаточная чистота процесса обработки, кроме брака, приводит к быстрой деградации ИС на этапе их функционирования. Чистота процессов сборки и обработки обеспечивается и соответствующей чистотой окружающей рабочей атмосферы, под которой понимают минимальную запыленность воздуха. В зависимости от допустимой запыленности производственные помещения делят на 5 классов. Предельная допустимая запыленность атмосферы производственного помещения (по ОСТ 11.ПО.050.001) сведена в табл. 1.5.4. Таблица 1.5.4
В помещениях 3-го и 4-го классов чистоты выполняют резку слитков полупроводникового материала, исследуют его физические свойства и надежность ИС. В помещениях 2-го класса чистоты осуществляют химическую обработку пластин, обработку ИС, контроль электрических параметров, шлифовку и полировку пластин, изготовление фотошаблонов. В помещениях первого класса чистоты выполняют наиболее ответственные операции: финишную очистку и отмывку пластин, фотолитографию, эпитаксиальное наращивание, диффузию примесей, вакуумное напыление. Производственные помещения должны удовлетворять определенным требованиям с точки зрения их расположения, внутренней отделки, герметичности, правил поведения и форм одежды персонала. Чистота окружающей среды проще и дешевле обеспечивается в ограниченном объеме, необходимом для выполнения той или иной операции. Поэтому ряд операций фотолитографии и сборки осуществляют в изолированных от окружающей среды устройствах – скафандрах, с помощью резиновых перчаток, герметично вмонтированных в скафандр. В скафандр подается специально очищенный воздух под небольшим избыточным давлением для уменьшения вероятности проникновения пыли извне в рабочий объем. Соединяя ряд скафандров герметичными каналами для передачи обрабатываемых изделий, создают технологические поточные линии (например, линии фотолитографии). Соответствующие требования предъявляются также к технологической таре для хранения и транспортировки полуфабрикатов. Для повышения точности, стабильности и воспроизводимости технологических операций обработки и контроля большое значение имеет микроклимат производственных помещений. По температурно-влажностным параметрам производственные помещения делятся на три класса (табл. 1.5.5). Таблица 1.5.5
Все перечисленные мероприятия, называемые вакуумной гигиеной, направлены на повышение технологической и эксплуатационной надежности микросхем. Определение глубины залегания p-n ререхода в полупроводниковых структурах Контроль глубины залегания р-n –переходов в полупроводниковых структурах как при их изготовлении, так и при исследовании полученных приборов в основном производится путем изготовления сферического или косого шлифа, заключающегося в удалении части материала и последующего декорирования химическими реагентами, обеспечивающими оптический контраст между р - и n -областью перехода. Определение границ областей производится с помощью микроскопа и переводных таблиц, а также вычисляется глубина расположения р-n –перехода под поверхностью полупроводниковой структуры. Кроме того, применим метод определения глубины залегания р-n –переходов в полупроводниковых структурах, основанный на неразрушающем характере проведения исследования, заключающийся в том, что информационным параметром глубины залегания перехода является характер изменения тока, протекающего через переход при определенном механическом давлении в локальной области перехода. Известно, что полупроводниковые структуры (диоды, транзисторы, многослойные структуры и т. п.) формируются на полупроводниковых материалах, кристаллическая решетка которых обладает, как правило, кубической или гексагональной симметрией. При приложении давления к кристаллу его симметрия нарушается, при этом происходит смещение частиц в пределах приложенной области давления, определяемой выражением
где v(x, y, z) – компоненты вектора смещения; G ij – тензор Грина; S – область воздействия давления; Р (х, у) – давление, производимое на поверхность S полупроводника с координатами x, у. Вычисление тензора Грина G tJ – отдельная задача, так как тензор зависит от приложенного усилия относительно выбранного кристаллографического направления и типа полупроводника. Установлено, что при приложении давления перпендикулярно плоскости х, у наиболее существенное влияние имеет компонента деформации x zz. Определено, что значение сдвиговой деформации x zz при воздействии на поверхность полупроводника, под которой расположена область р-n –перехода индентером с радиусом контактируемой поверхности R, равно
где Y – модуль Юнга; s – коэффициент Пуассона; F – приложенное усилие. Зонная структура энергетических уровней некоторых полупроводников, как известно, обладает многодолинностью. Например, зона проводимости кремния имеет шесть минимумов, экстремумы которых находятся на различных кристаллографических направлениях и расположены вблизи границ зоны Бриллюэна, составляя величину 0,8 k, где вектор k =1 соответствует границе зоны Бриллюэна. Валентная зона кремния имеет два максимума, расположенных в центре зоны Бриллюэна, что соответствует значению волнового вектора k =0. Расстояние между экстремальными точками зоны проводимости и валентной зоны составляет ширину зоны проводимости. При давлении на полупроводник энергия одних минимумов зоны проводимости увеличивается, других – уменьшается, например, для кремния при действии силы, приложенной перпендикулярно плоскости {111}, один из минимумов смещается к краю зоны Бриллюэна в направлении плоскости {100} и при этом сдвиговая деформация xzz с изменением приложенной силы приводит к изменению сил взаимодействия между атомами кристаллической решетки, что вызывает расщепление экстремума и, как следствие этого, – изменение спектра носителей, так как энергия носителей в любой n -ной зоне регулярной структуры полупроводника является функцией волнового вектора k. Смещение энергетических уровней на локальном участке полупроводника, находящегося в области давления, определяется в основном распределением компонентов тензора деформации. Например, энергетические уровни зоны проводимости и валентной зоны, расположенные в центре зоны Бриллюэна, максимально смещаются к центру области приложения силы, а энергетические уровни, минимумы которых находятся в других точках k – пространства, имеют более сложный характер распределения, так как их смещение зависит от угла, определяемого проекцией соответствующих осей на плоскость {111}, на которой, как правило, в основном формируются все структурные элементы современной микроэлектроники. Ток через р-n –переход, сформированный в полупроводниковом материале, определяется соотношением
где I s – ток насыщения; е – заряд электрона; U – напряжение, приложенное к р-п переходу; k – постоянная Больцмана; T - температура в градусах Кельвина. Ток насыщения выражается через
где L nи t п – длина свободного пробега и время жизни электрона; L pи t p – длина свободного пробега и время жизни дырок; п poи p no – соответственно концентрация электронов в р -области и дырок в п -области. Факторами, обуславливающими изменение характеристик приборов под воздействием давления, являются смещение энергетических уровней и изменение спектра носителей зарядов, изменение эффективной массы носителей зарядов, времени их жизни, а также возникновение обратимых центров рекомбинации. Так как изоэнергетическими поверхностями вблизи экстремумов зоны проводимости и валентной зоны являются эллипсоиды вращения, то для монокристаллов полупроводников, обладающих многодолинной структурой энергетических зон, эффективная масса носителей в зоне проводимости определяется как
где m -масса свободного электрона; Z – количество минимумов в зоне проводимости; m l и m t – продольная и поперечная эффективные массы электрона, соответствующие составляющим эллипсоидов вращения, отвечающих экстремальным участкам энергетических зон. При воздействии давления зоны расщепляются и электроны проводимости перетекают на уровни, имеющие минимальную энергию, происходит изменение распределения эффективных масс m lи m tв долинах зоны проводимости, подвижности носителей, их времени жизни, смещение энергетических уровней и изменение ширины запрещенной зоны, а в итоге это приводит к изменению концентрации неосновных носителей тока р пи п р.Так как плотность тока насыщения Js определяется именно этими носителями, как это следует из выражения
где m n, m p, t n, t p –подвижность и время жизни носителей, соответствующих приведенным индексам, а концентрация электронов оценивается по
где h – постоянная Планка; Е с, E F – соответственно уровень зоны проводимости и уровень Ферми, то ток через р-n –переход (1.5.6) непосредственно зависит от этих составляющих. Ток насыщения р-n –перехода при воздействии на него усилия, когда изменение ширины запрещенной зоны D Eg сравнимо с энергией kТ дает значительный вклад в изменение тока через исследуемый переход. Проведя некоторые преобразования и подставляя (1.5.3) и (1.5.4) в (1.5.5), а также учитывая многодолинность рассматриваемой энергетической структуры материала полупроводника, выражение для отношения электронных токов при деформации к току в отсутствие деформации принимает вид
где D E v – приращения вершин валентной зоны, учитываемые при деформации; D E ci – приращения минимумов зоны проводимости при деформации; m j, m v – значения эффективных масс, соответствующие сблизившимся экстремумам зоны проводимости и валентной зоны; m n, t n – соответственно подвижность и время жизни электронов при деформации; m no, t no – подвижность и время жизни электронов в отсутствие деформации; М – число экстремумов зоны проводимости; N – число экстремумов валентной зоны. Уровни смещения валентной зоны и зоны проводимости зависят от распределения производимых деформаций в области р-n –перехода. Под острием индентера деформируется не весь переход, а только его часть, находящаяся в непосредственном соприкосновении контактирующего круга тела индентера с поверхностью полупроводника. Площадь этой контактирующей поверхности определяется как
где R – радиус закругления иглы индентера; F – усилие, приложенное к индентеру; D – деформационный потенциал,
здесь индексы при коэффициентах Пуассона и модуля Юнга соответственно относятся к материалу полупроводника и индентера. Выражение (1.5.9) справедливо для случая, когда деформации подвержен весь переход, а если усилие приложено только лишь к части перехода в локальной области, задача осложняется, поскольку необходимо учитывать вклад составляющих тока под индентером и остальной частью перехода, не испытывающей давления. Для полного тока р-n –перехода при локальном давлении можно записать
где J o – плотность тока через р-n –переход вне контакта с индентером (деформация отсутствует); J p – плотность тока на участке р-n –перехода, контактирующего с индентером; А – общая площадь р-n –перехода. Наибольшее отношение токов (1.5.8) имеет место при максимальной нагрузке (при давлении на всю площадь перехода оно может достигать трех и более порядков). Для того, чтобы приложенная к индентеру внешняя сила не вызвала необратимых явлений в исследуемых полупроводниковых структурах, необходимо стремиться не превышать предела упругости, значение которой для каждого вида полупроводника является индивидуальной величиной. Учитывая (1.5.8) и (1.5.11), условие для определения верхней границы величины давления, производимого индентером, выбираемого из соображений предотвращения необратимых изменений вольт-амперных характеристик р-n перехода, принимает вид
здесь l – глубина расположения р-n –перехода под поверхностью пластины. На рис. 1.5.1 представлено сечение полупроводниковой структуры со сложным профилем р-n –перехода и сканирующим индентером. Для определения глубины расположения р-n –перехода к областям 3 и 4 пластины 1 прикладывается напряжение, смещающее переход 2 в прямом направлении (плюс источника питания подводится к р -области) и фиксируется ток через него. Затем перпендикулярно поверхности пластины 1 посредством приложения силы F к индентеру 5 производится давление в локальной области р-n –перехода. При фиксированном значении силы, приложенной к индентеру, и смещающем напряжении постоянной величины отношение токов (1.5.8) через р-n –переход является функцией глубины, определяемой по градуировочной кривой. На рис. 1.5.2 представлено отношение токов при сканировании структуры, изображенной на рис. 1.5.1. Как следует из рис. 1.5.2, зависимость этого отношения от глубины расположе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.82 (0.016 с.) |

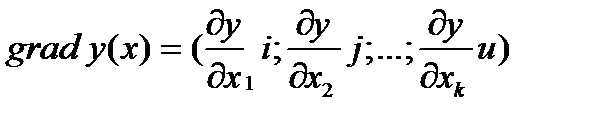 ,
,
 .
.
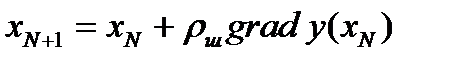 ,
,

 .
.

 ,
,
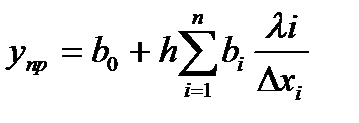 .
.
 .
.

 ;
; 

 .
.
 .
.

 G ij(x – x’, y – y’, z) P j(x’, y’, z) dx’dy’,
G ij(x – x’, y – y’, z) P j(x’, y’, z) dx’dy’,
 m ei3/2 exp [(E Ci– E F)/ kT ],
m ei3/2 exp [(E Ci– E F)/ kT ],
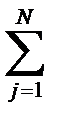
 (m j/ m v)3/2×
× exp [(D E vj–D E ci)/ kT ]}/ M,
(m j/ m v)3/2×
× exp [(D E vj–D E ci)/ kT ]}/ M,
 ,
,
 j p(x, y) dxdy,
j p(x, y) dxdy,
 /2 p
/2 p  ],
],



