
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начала математического анализаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте СОДЕРЖАНИЕ
Цели и задачи дисциплины – требования к результатам освоения дисциплины: В результате изучения математики обучающийся должен Знать/понимать • значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе; • значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; • универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; • вероятностный характер различных процессов окружающего мира; АЛГЕБРА Уметь • выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; • проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции; • вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства; ФУНКЦИИ И ГРАФИКИ Уметь • определять значение функции по значению аргумента при различных способах задания функции; • строить графики изученных функций; • описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функциинаибольшие и наименьшие значения; • решать уравнения, простейшие системы уравнений, используя свойства функцийи их графиков; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков; НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА Уметь • вычислять производные и первообразныеэлементарных функций, используя справочные материалы; • исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа; • вычислять в простейших случаях площади с использованием первообразной; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения; УРАВНЕНИЯ И НЕРАВЕНСТВА Уметь • решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы; • составлять уравнения и неравенствапо условию задачи; • использовать для приближенного решения уравнений и неравенств графический метод; • изображать на координатной плоскости множества решений простейших уравнений и их систем; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • построения и исследования простейших математических моделей; ТЕОРИИ ВЕРОЯТНОСТЕЙ Уметь • решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; • вычислять в простейших случаях вероятности событий на основе подсчета числа исходов; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • анализа реальных числовых данных, представленных в виде диаграмм, графиков; • анализа информации статистического характера; ГЕОМЕТРИЯ Уметь • распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; • описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении; • анализировать в простейших случаях взаимное расположение объектов в пространстве; • изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; • строить простейшие сечения куба, призмы, пирамиды; • решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); • использовать при решении стереометрических задач планиметрические факты и методы; • проводить доказательные рассуждения в ходе решения задач; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур; • вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства Тематический план по учебнику «Математика» Начальное и среднее профессиональное образование Башмаков М.И. Количество часов – 295
Формы и процедура текущего и промежуточного контроля по базовой общеобразовательной дисциплине «Математика», для обучающихся I курса. На первом курсе количество часов по программе составляет: 148 часов. Включает изучение следующих разделов:
По теме: «Перпендикулярность прямых и плоскостей» предусмотрена письменная контрольная работа на 45 минут. По окончании разделов предусмотрен текущий контроль в виде:
По окончании 1 семестра предусмотрен промежуточный контроль в виде теста, состоящего из 10 вопросов, с решением задач, рассчитанного на 40 минут, в виде контрольных измерительных материалов по темам: «Развитие понятия о числе», «Корни, степени и логарифмы», «Прямые и плоскости в пространстве». По окончании II семестра предусмотрен промежуточный контроль в виде теста, состоящего из 10 вопросов, с решением задач, рассчитанного на 40 минут, в виде контрольных измерительных материалов по темам: «Развитие понятия о числе», «Корни, степени и логарифмы», «Прямые и плоскости в пространстве», «Комбинаторика», «Координаты и векторы», «Основы тригонометрии», «Функции и графики». Результаты работ контрольного характера отражаются в учебном журнале. Обучающиеся, получившие неудовлетворительную оценку за тест, обязаны переписать ее в течение 10 дней. Формы и процедура текущего и промежуточного контроля по базовой общеобразовательной дисциплине «Математика», для обучающихся 2 курса. На втором курсе количество часов по программе составляет: 147 часов. Итого по программе: 295 часов. Включает изучение следующих разделов: 1. Многогранники и круглые тела. 2. Начала математического анализа. 3. Интеграл и его применение. 4. Элементы теории вероятностей и математической статистики. 5. Уравнения и неравенства. 6. Повторение По темам: «Применение производной к исследованию функций», «Интеграл и его применение», «Уравнения и неравенства» предусмотрена письменная контрольная работа на 45 минут. По окончании разделов предусмотрен текущий контроль в виде: 1. Тестирования по теме: «Многогранники»
По окончании изучения разделов и повторения пройденного за 2 курса обучения предусмотрен итоговый контроль в виде: письменной экзаменационной работы, за курс средней школы, рассчитанной на 5 академических часов. Результаты работ контрольного характера отражаются в учебном журнале. Обучающиеся, получившие неудовлетворительную оценку за тест, обязаны переписать ее в течение 10 дней. Тема: «Понятие о числе» Выберите правильный ответ.
а)
а) -1 б) -3 в) 0 г) 9
а) 4 і -8 б) 3 і +5 в)2 і -4 г) 2 і +4
а) 2 б) 6
а) нет корней б) 4 в)
а)
а) 6 - 2
а) z z 9.Вычислите: (-1+ а) 210 б) 2-10 в) 211 г) 212 10.Решите уравнение: z а)
б) в) z г) z
Тема: «Комбинаторика» Выберите правильный ответ. 1. Сколько двузначных чисел можно составить, используя цифры 4; 5 и 3? а) 3; б) 9; в) 6; г) 12. 2. Во сколько раз число размещений 9 объектов на трех местах меньше числа размещений тех же объектов на пяти местах? а) в 20 раз б) в 30 раз в) в 23 раза г) в три раза 3. Пусть множества А, В и С – числовые промежутки, причем А = [-7; -2], В = [-3; 4], С = [0;5]. Найдите: А U В U С. а) [-7;-3]; б) [-3;0]; в) [-7;5]; г) [-2;5]. 4. Пусть множества А, В и С – числовые промежутки, причем А = [-5; 1], В = [0; 8]; С = [-3;10]. Найдите А а) [-7;1]; б) [0;1]; в) [-2;8]; г) [-5;10] 5. Вычислите: Р₄ а) 4; б) 24; в) 4!; г) 20. 6. Вычислите: а) в) 7. Вычислите: С а) в) 8. Чему равна сумма биноминальных коэффициентов для: (х+1)7 а) 32 б) 8 в) 128 г) 16 9. Сколькими способами из 10 игроков волейбольной команды можно выбрать стартовую шестерку? а) 9 б) 210 в) 8 г) 64 10. По формуле бинома Ньютона раскройте скобки: (х+1)⁵. а) х³ + 27; б) х³ + 3х² + 3х + 27; в) х5 + 10х4 + 10х2 + 1; г) х5 + 5х4 +10х3 + 10х2 + 5х + 1.
Тема: «Функции и графики» Выберите правильный ответ. 1. Укажите рациональную функцию: а)y=k x + b б)y=a2x2+a1x+a0 в)y= 2. Какая из функций имеет точку разрыва: а) у= -3х2-6х+3 б) у= sinх в) у= lgх г) у= 3. График функции у = а) возрастает; б) параллелен оси х; в) убывает; г) параллелен оси у. 4. Как связаны между собой области определения функции у= а) графики симметричны относительно начала координат б) графики симметричны относительно оси Оу в) графики симметричны относительно оси Ох г) графики совпадают 5. Найдите область определения функции y= а) (-1;∞) б) (0;∞) в) (-∞;0) г) (1;∞) 6. Найдите период функции f(x)= sin4x cos x – cos 4x sin x: а) 3π б) 7. Найдите промежутки возрастания функции f(х) = 0,5cos x -1: а) в) 8. Исследуйте функцию f(x)=2x2sinx, на четность: а) нечетная б) четная в) ни четная ни нечетная. 9. Как будет меняться график функции у=kf(х), при изменении параметра k: а) параллельный перенос по оси абсцисс на вектор (а;0) б) растяжение вдоль оси абсцисс в) растяжение вдоль оси ординат в k раз г) параллельный перенос по оси ординат на вектор (0;b) 10. Какие из функций имеет асимптоты: а) у=х3 б) у=
Тема: Многогранники Выберите правильный ответ. 1. Выберите основную формулу для вычисления площади полной поверхности призмы: а) Sп.п. = 2Sосн + Sб.п.; в) Sп.п. = Sосн + 2Sб.п; б) Sп.п. = Sосн + Sб.п; г). Sп.п. = Sосн ∙ H. 2. Определите формулу для вычисления диагонали прямоугольного параллелепипеда по трем его измерениям: а) d = a + b + c; в) d² = a² + b² + c²; б) d = a b c; г) d = ½ a b c. 3. Выберите формулу для вычисления объема призмы: а) V = Sосн ∙ H; в) V = ⅓ Sосн ∙ H; б) V = a b c; г) V = a + b + c. 4. Выберите формулу для вычисления объема пирамиды: а) V = Sосн ∙ H; в) V = ⅓ Sосн ∙ H; б) V = a b c; г) V = (a + b) ∙ H. 5. Диагональным сечением наклонного параллелепипеда является: а) прямоугольник; в) четырехугольник; б) квадрат; г) параллелограмм 6. Найдите объем прямоугольного параллелепипеда со сторонами: 5см, 8см и 12см. а) 156 см³; в) 25 см; б) 7. Найдите диагональ прямоугольного параллелепипеда по трем его измерениям: 2см, 3см и 6см. а) 11 см; в) √11 см; б) 7 см; г) 49 см. 8. Найдите площадь диагонального сечения прямоугольного параллелепипеда по трем его измерениям: 3см, 4см и 6см. а) 72 см²; в) 150 см²; б) 30 см²; г) 42 см. 9. Найдите площадь полной поверхности четырехугольной призмы, если стороны основания равны 8дм и 5дм, а высота 11дм. а) 143 дм²; в) б) 210 дм²; г) 366 дм². 10. Найти высоту правильной четырехугольной пирамиды, если основание пирамиды равно 2см, а боковое ребро равно 3см. а) 11 см; в) б)
Тема: «Тела вращения». Выберите правильный ответ. 1. Выберите основную формулу для вычисления объема конуса: а) V = π R² H; в) V = ⅓ π R² H; б) V = a b c; г) V = 2 π R H.
2. Выберите основную формулу для вычисления объема цилиндра: а) V = π R² H; в) V = ⅓ π R² H; б) V = 2π R H; г) V = a b c. 3. Определите: какая геометрическая фигура является диаметральным сечением шара? а) эллипс; в) окружность; б) круг; г) сфера. 4. Определите: какой геометрической фигурой является сечение, параллельное оси цилиндра? а) треугольник; в) прямоугольник; б) круг; г) параллелограмм. 5. Определите: какая геометрическая фигура является основанием наклонного цилиндра? а) окружность; в) прямоугольник; б) эллипс; г) круг. 6.Найти полную поверхность конуса, если: R= 4 см.; ℓ= 6 см. а) 40π см²; в) 24π см²; б) 48π см²; г) 10π см². 7. Радиус основания цилиндра 4см, а высота 6см. Найдите диагональ осевого сечения. а) 14 см; в) б) 10 см; г) 8. Радиус основания конуса 2см, а высота 7см. Найдите образующую. а) 4 см; в) √11 см; б) 3 см; г) √53 см. 9.Усеченный конус, радиус оснований равен 10м и 4м требуется превратить в равновеликий цилиндр такой же высоты. Найти диаметр основания этого цилиндра. а) 28 м; в) 4 б) 10. Шар, радиус которого равен 20см, пересечен плоскостью на расстоянии 4см от центра. Найдите площадь сечения а) 384π см²; в) 80π см²; б) 24π см²; г) 160π см². Модуль 6. Комбинаторика 1. Из истории комбинаторики. 2. Задача де Мере. 3. Бином Ньютона. 4. Треугольник Паскаля. Интеграл и его применение. 1. Что такое интеграл. 2. Плотность интегральной величины. 3. Интегральные суммы. 4. Рефераты по темам: «История вывода формулы Ньютона-Лейбница». 5. Задачи на вычисление неопределенного интеграла. 6. Задачи на вычисление площади поверхности пространственного тела 7. Задачи на вычисление объемов тел. Уравнения и неравенства. 1. Разрешимость алгебраических уравнений. 2. К.Ф.Гаусс и его труды. 3. Жозеф Луи Лагранж и его труды 4. Системы и совокупности уравнений. 5. Графическое решение уравнений. 6. Графическое решение неравенств. 7. Графическое решение систем уравнений. 8. Исследование системы двух линейных уравнений с двумя неизвестными. 9. Решение системы двух линейных уравнений с двумя неизвестными. 10. Решение уравнений повышенной сложности. 11. Решение систем уравнений повышенной сложности. Список литературы Учебники: основной: Начальное и среднее профессиональное образование «Математика» Башмаков М.И. (М.: Академия, 2012)
дополнительные: 1.«Алгебра и начала анализа 10 - 11» Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П., Ивлев Б.М.,Шварцбурд С.И.. (М.: Просвещение, 2008 и последующие издания) 2.«Геометрия 10 - 11» Погорелов А.В.(М.:Просвещение, 2010 и последующие издания)
Дополнительная литература 1. С.М.Никольский «Алгебра» пособие для самообразования (М.:Наука, 1984) 2. П.В.Стратилатова «Из опыта преподавания математики» сборник статей (М.:ГУПИ Мин.пр. РСФСР, 1955) 3. Е.С.Кочетков «Алгебра и элементарные функции» уч.пособие (М.:Просвещение, 1972) 4. М.И.Башмаков «Математика» уч.пособие (М.:Высшая школа, 1987)
СОДЕРЖАНИЕ
Цели и задачи дисциплины – требования к результатам освоения дисциплины: В результате изучения математики обучающийся должен Знать/понимать • значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе; • значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; • универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; • вероятностный характер различных процессов окружающего мира; АЛГЕБРА Уметь • выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; • проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции; • вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства; ФУНКЦИИ И ГРАФИКИ Уметь • определять значение функции по значению аргумента при различных способах задания функции; • строить графики изученных функций; • описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функциинаибольшие и наименьшие значения; • решать уравнения, простейшие системы уравнений, используя свойства функцийи их графиков; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков; НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА Уметь • вычислять производные и первообразныеэлементарных функций, используя справочные материалы; • исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа; • вычислять в простейших случаях площади с использованием первообразной; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения; УРАВНЕНИЯ И НЕРАВЕНСТВА Уметь • решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы; • составлять уравнения и неравенствапо условию задачи; • использовать для приближенного решения уравнений и неравенств графический метод; • изображать на координатной плоскости множества решений простейших уравнений и их систем; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: • построения и исследования простейших математических моделей;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 б)
б) 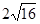 в)
в)  г)
г) 


 г) -2
г) -2
 г)
г) 
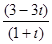
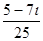 б) -3
б) -3 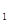 =2 -
=2 -  =2+
=2+ 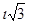 )
) 






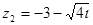

 .
. ∙
∙ 
 ∙
∙  ; г) 5.
; г) 5.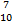 ∙ Р₃
∙ Р₃ ∙ 3!; б) 720;
∙ 3!; б) 720; ; г) 5040.
; г) 5040. г) y=x r
г) y=x r

 и у=
и у=  :
: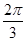 в) 2
в) 2  г) 2
г) 2 б)
б) 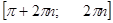
 г)
г) 
 - 4 в) у= 2х г) у=
- 4 в) у= 2х г) у= 
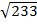 см²; г) 480 см³.
см²; г) 480 см³.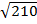 дм;
дм; см;
см; см; г) 6 см.
см; г) 6 см.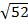 см;
см; см.
см. м;
м; м; г)
м; г)  м.
м.


