
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ моделируемой системы и постановка задачСодержание книги
Поиск на нашем сайте
Методология моделирования Для получения математических моделей можно использовать пассивный или активный эксперименты. Пассивный эксперимент сводится только к наблюдениям за протеканием процесса в объекте исследования и регистрации его характеристик. Активный эксперимент допускает вмешательство в ход процесса и соответственно с этим организацию наблюдений. Моделирование можно рассматривать как процесс, состоящий из искусства и науки, который основывается на основном принципе диалектического познания природы: «от простого созерцания к абстрактному мышлению и от него к практике». Математический аппарат моделирования основывается на теории вероятностей и математической статистики. Достоверность результатов моделирования обеспечивается соблюдением технологии моделирования СОИ, разработанной для его проведения (рис. 1.3). ОИ – объект исследования, которым является моделируемая система. На первом этапе производят анализ моделируемой системы и постановку задач. Второй этап – формализация. Следуя по центральной ветви, которая выбирается на втором этапе, если имеющихся данных не достаточно и невозможно осуществить аналитическое моделирование (это активный эксперимент и имитационная модель (АЭИМ)) будем последовательно выполнять следующие этапы. На третьем этапе разрабатывается имитационная модель (РИМ). На четвертом оценивается пригодность модели (ОПМ). На пятом производится планирование эксперимента (ПЭ). На шестом производится статистический анализ (СА). Статистический анализ в зависимости от поставленных задач может включать в себя процедуры оценки однородности статистических данных, регрессионного, факторного и кластерного анализа. На седьмом производится оценка степени влияния факторов (ОСВФ), прогнозирование (ПР) и оптимизация (ОПТ). На втором этапе может быть принято решение, что имеющихся статистических данных достаточно для проведения статистического анализа и построения регрессионной модели. В этом случае идем по стрелочке пассивный эксперимент, регрессионная модель (ПЭРМ). Если же исходных данных об ОИ недостаточно, но есть возможность их получить на натурном образце без построения математической модели идем по стрелочке активный эксперимент, регрессионная модель (АЭРМ). Если имеющихся статистических данных о функционировании ОИ недостаточно и имеется возможность создания аналитической модели, то идем по верхней ветке. Это пассивный эксперимент и аналитическая модель (ПЭ АМ). В этом случае выполняются следующие этапы. На этапе 3l составляется граф-схема переходов (РГСП) и по ней система уравнений переходов (СУП). На этапе 4l производится построение вероятностных формул (ПВерФ). На этапе 5l получают количественные формулы (ПКФ). На этапе 6l получают временные формулы (ПВрФ). Результаты моделирования возвращаются к ОИ по стрелочке «интерпретация», которая заключается в установлении соответствия между формальной моделью и объектом исследования.
Второй этап моделирования. Формализация. Корреляционный анализ Корреляция – это соотношение (взаимозависимость) случайных величин между собой. В качестве количественной меры оценки взаимосвязи между случайными величинами используется коэффициент линейной корреляции, вычисляемый для случайных величин х и у по n экспериментальным данным по следующей формуле.
Оценить существенность коэффициента линейной корреляции между случайными переменными по критерию Стьюдента можно при условии, что распределения этих случайных величин подчиняется нормальному закону и что они имеют совместное двумерное нормальное распределение. Коэффициент линейной корреляции является случайной величиной, и поэтому для него может быть вычислена стандартная ошибка
Тест частот Функция распределения равномерно распределенных случайных чисел в диапазоне от 0 до 1 представлена на рис.14.1, а функция плотности на рис.14.2.
Вычисляется критерий согласия c2, с количеством степеней свободы R.
Тест разрядов Для равномерного закона вероятность появления любого символа в любом разряде числа одинакова. Для десятичных чисел она равна 0,1; для двоичных – 0,5. Для проведения тестирования подсчитывается количество каждых символов в каждом разряде числа, то есть их частоты. И аналогично предыдущему вычисляется критерий c2 и количество степеней свободы R. А далее проверяем попадание коэффициента доверия гипотезе в 10%-ный доверительный интервал. При отрицательном результате гипотеза отвергается. Тест оценки случайности
Коэффициент линейной автокорреляции меняется от -1 до +1. Приведем формулу для вычисления критического значения коэффициента автокорреляции: где n – количество пар случайных чисел; tкрит – критическое значение критерия Стьюдента, взятое по статистическим таблицам для рекомендуемого уровня значимости a=0,05 для количества степеней свободы n-2; rкрит – критическое значение коэффициента линейной автокорреляции и если вычисленное значение не меньше критического, то связь между переменными считается существенной. Если же вычисленное значение по абсолютной величине не меньше 0,8
Тест периодичности Тест периодичности заключается в вычислении длины периода и длины отрезка апериодичности. Период – это количество повторяющихся чисел, а отрезок апериодичности – это такая последовательность случайных чисел, в которой нет ни одной пары одинаковых чисел, но следующее число за отрезком апериодичности имеет в нем «свою» пару. Для корректного проведения имитационного моделирования и получения достоверных результатов требуется использовать случайные числа только на отрезке апериодичности, потому что любое повторение случайных чисел искажает получаемые результаты. Для вычисления длины периода используется следующий метод: генератор случайных чисел по интуиции выводится за пределы отрезка апериодичности, то есть на совокупность случайных чисел, в которой имеются периоды. Затем запоминается очередное случайное число, а каждое последующее число сравнивается с числом, которое запомнили. Количество случайных чисел до совпадения случайного числа с числом, которое запомнили, будет являться длиной периода. Для определения длины отрезка апериодичности берется два одинаковых генератора. После того, как первый из них выработает количество чисел равное длине периода, запускается второй генератор, и пары вырабатываемых ими чисел сравниваются между собой до тех пор, пока сравнение не даст положительный результат. После этого подсчитывается количество чисел, выработанных первым генератором. Это и есть длина отрезка апериодичности, и чем качественнее генератор, тем больше длина его отрезка апериодичности.
Планирование имитационных экспериментов. Концепция «черного ящика» Планирование экспериментов Цель планирования экспериментов – получение результатов с требуемой достоверностью при наименьших затратах. Планирование подразделяется на стратегическое и тактическое. Стратегическое планирование Для стратегического планирования будем использовать концепцию «черного ящика», суть которого – абстрагирование от физической сущности процессов, происходящих в моделируемой системе и выдаче заключений о ее функционировании только на основании входных и выходных переменных. Входные, независимые переменные называются факторами. Выходные – откликами, их величина зависит от значений факторов и параметров ОИ. Структурная схема чёрного ящика представлена на рис.15.1. Х1
ХМ.. YК xm При использовании концепции чёрного ящика должны выполняться следующие условия. 2.Одновременное изменение всех факторов. Обеспечивает уменьшение стандартной ошибки при проведении экспериментов. 3.Последовательность планирования. Проведение экспериментов подразделяется на ряд последовательных этапов и планировние каждого последующего этапа производится с учётом результатов, полученных на предыдущих этапах. 4. Кодирование. Не обязательно. Кодирование значительно упрощает расчёты и делает анализ результатов более наглядным, что весьма существенно при «ручной» обработке результатов. При применении ЭВМ кодирование также представляет некоторые преимущества в анализе результатов. К факторам предъявляют следующие требования. 1. Легкая управляемость, что позволяет сравнительно несложно повторять проводимые эксперименты. 2. Факторы не должны являться функциями каких-то аргументов. 3. Факторы должны быть хотя бы линейно независимыми между собой, что позволяет упростить математическую модель, не вводя в неё произведения факторов между собой. 4. Любое сочетание факторов в стратегических планах не должно выводить объект из допустимого режима функционирования.
9.План ДФЭ (дробных факторных экспериментов).
10. РЦКП (ротатабельный центральный композиционный план). РЦКП обеспечивает незначимую величину ошибки в точках, равноотстоящих от центра проведения экспериментов, поэтому они широко применяются в динамических методах поиска экстремальных значений. Расстояние звёздной точки от центра осей координат и количество проводимых экспериментов в центральной точке вычисляются по формулам:
Композиционные планы ОЦКП и РЦКП имеют существенный недостаток, который начинает сказываться с увеличением количества факторов в проводимых экспериментах, чем больше факторов, тем больше расстояние звёздных точек от центра осей координат, которое всё больше и больше удаляется от заданных границ диапазонов изменения факторов, что является нежелательным.
11.Д–оптимальные планыВ D – оптимальных планах значения факторов не выходят за установленные границы диапазонов их изменения. Кроме того они обладают ещё одним существенным достоинством, обеспечивая минимальную ошибку во всём принятом диапазоне изменения факторов. На практике наиболее часто применяются планы Коно и планы Кифера. Планы Коно Для многофакторных экспериментов в геометрической интерпретации диапазон изменения факторов представляется многомерным кубом, который далее будем называть просто куб. Для двух факторов этот куб вырождается в квадрат. Эксперименты по плану Коно проводятся в вершинах куба, серединах рёбер и центре куба. Характерной особенностью D – оптимальных планов является разница в количестве проводимых экспериментов для точек плана различного вида. Удельные веса видов точек для двухфакторных экспериментов в планах Коно приняты следующие. 1. Вершины куба - 2. Середины ребер - 3. Центр куба - Расположение точек стратегического плана на квадрате и кубе представлено на рис.15.3.
Рис.15.3. Геометрическая интерпретация двухфакторного плана на квадрате и трёхфакторного – на кубе
Планы Кифера Эксперименты по плану Кифера проводятся в вершинах куба, серединах рёбер и центрах граней. Для двухфакторных экспериментов по плану Кифера приняты следующие удельные веса. 1. Вершины куба - 2. Середины рёбер - 3. Центры граней - Расположение точек плана для двухфакторных экспериментов представлено на рис.15.4; для трёхфакторных на рис.15.5.
план Кифера, которые позволяют построить математическую зависимость вида:
Отметим что для того, чтобы не потерять корректность D – оптимальных планов, чтобы количество реализаций в каждом варианте было целым числом, общее количество проводимых экспериментов для планов Коно требуется брать точно кратным 1000 а для планов Кифера – кратным 10000.
12.Тактическое планирование имитационных эксперементов Центральная предельная теорема утверждает, что сумма достаточно большого количества случайных чисел, выработанных при достаточно общих условиях, подчинена нормальному закону вне зависимости от того какому закону подчинены сами случайные числа При этом соблюдается следующее соотношение математического ожидания и среднего квадратического отклонения между введенным и исходным распределением: При выводе формулы для вычисления количества реализаций в эксперименте проведена замена вероятности попадания нормально распределённой случайной величины от минус бесконечности до левой границы доверительного интервала, ввиду симметричности нормального закона, на вероятность попадания от правой границы доверительного интервала до плюс бесконечности, то есть на величину
требуется задаться доверительной вероятностью β. Рекомендуемое значение: β=0,95. По статистическим таблицам находим
Вероятность β в (15.13) показывает, что разность случайной величины Х и ее математического ожидания по абсолютной величине меньше, или равно сколь угодно малому положительному числу ε, не меньше, чем величина Возьмем вместо переменной Х оценку математического ожидания Преобразуя получим формулу для вычисления количества реализаций случайной величины для получения результатов с заданной достоверностью. Если по результатам моделирования с заданной достоверностью требуется оценить вероятность какого-либо события, то считают, что с вероятностью р событие наступает и равно 1, и с вероятностью (1-р) событие, равное 0, не наступает, тогда Тогда по центральной предельной теореме:
по неравенству Чебышева: Полученные формулы позволяют вычислять требуемое количество реализаций случайного процесса в моделируемых вариантах систем при тактическом планировании. 13.Основные свойства языка GPSS W. В GPSS W имеется два специализированных языка. · Язык высокого уровня, предназначенный для описания объектов моделирования, это операторы GPSS W · Язык низкого уровня – это PLUS-операторы, ориентированные на вычисления и управление экспериментом. В качестве операторов имитационной модели можно одновременно использовать операторы GPSS W и PLUS-операторы. Операторы GPSS W подразделяются на блоки и команды. Блоки – это операторы, которые исполняют возложенные на них функции при входе в них движущихся объектов, называемых транзактами. Команды предназначены для определения параметров некоторых объектов модели и управления процессом моделирования. Операторы GPSS W состоят из 53 блоков и 25 команд. Состояние объектов модели в процессе моделирования отображается 35 системными числовыми атрибутами (СЧА). К СЧА можно обращаться из любых операторов GPSS W. Операторы GPSS W имеют единый формат записи, состоящий из следующих полей: 1. Поля метки, в котором указывается либо имя объекта, либо натуральная метка для организации перехода транзакта. 2. Поля операции, в которое записывается либо тип объекта, либо вид выполняемой операции. 3. Поля операндов, в которое записываются параметры объекта. В некоторых операторах записывается вычисляемое математическое выражение. В зависимости от типа оператора, изменяется количество операндов и их назначение. Любая запись после поля операндов, сделанная с пробелом не менее, чем в одну позицию считается комментарием. Кроме того, комментарий можно записать с новой строки после символа
Принцип ближайшего соседа.
Принцип медианы.
Генерации случайных чисел 1.Метода реализуется сравнительно несложными программными процедурами. 2.Аналитический метод не имеет методической ошибки, но в полученные с его помощью формулы входят процедуры, требующие определенных затрат машинного времени.
Метод Ньютона. Для решения оптимизационных задач с нелинейными функциями можно использовать метод Ньютона (метод касательных). Метод Ньютона требует, чтобы оптимизируемая функция была дважды дифференцируема. В экстремальной точке производная функции
,
Вычисления 1. Если начальное приближение 2. Если начальное приближение Для вычисления шага изменения значения аргумента
1. Временные динамические ряды. основные понятия. проверка гипотез о существовании тенденций. Временные ряды Временными динамическими рядами (ВДР) называются статистические данные, отображающие развитие изучаемого процесса (явления) во времени. В качестве фактора в ВДР используются либо даты, либо интервалы времени. В качестве отклика – количественные показатели развития изучаемого процесса во времени. Основная цель статистического изучения временных динамических рядов (ВДР) состоит в выявлении и оценивании закономерностей их развития. Основные показатели динамики ВДР 1. Базисный абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
2. Цепной абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
3. Базисный темп роста, вычисляется делением сравниваемого уровня на уровень, принятый за базу:
4. Цепной темп роста, вычисляется делением сравниваемого уровня на предыдущий:
5. Базисный темп прироста – вычисляется делением базисного абсолютного прироста
6. Цепной темп прироста – вычисляется как отношение сравниваемого цепного абсолютного прироста
7. Средний уровень ВДР (оценка математического ожидания): § для интервального ряда:
§ для моментного ряда с равностоящими датами:
§ для момента ряда с неравностоящими датами:
8. Средний абсолютный прирост:
9. Средний темп роста:
10. Средний темп прироста:
Проверка гипотезы о существовании тенденции Проверка разности средних уровней: Разбиваем анализируемый ряд на две примерно одинаковые выборки, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность. Принимаем допущение, что выделенные выборки подчиняются нормальному закону (можно проверить в ППП Statistica). Воспользуемся методикой, разработанной для малых выборок. Находим средние значения для левой выборки
число степеней свободы Принимаем уровень значимости по рекомендации
где S – среднее квадратическое отклонение разности средних.
При уровне значимости Если
Сглаживание Суть сглаживания сводится к замене фактических уровней ВДР расчётными, имеющими меньшие колебания, чем исходные данные. На практике наиболее часто используют следующие методы: 1. Скользящих средних 2. Взвешенных скользящих средних 3. Экспоненциальный Метод скользящих средних Выбирается интервал сглаживания – нечётное число
Так как каждый раз мы добавляем 1 новый член и 1 вычитаем, то другая запись в виде скользящей средней:
Три свойства скользящих средних 1. Уменьшение нерегулярности колебаний в ряде 2. Чем больше 3. Смещение сглаженных значений 4. Пропадание начальных и конечных значений ряда (концы таблиц) 5. Если требуется сгладить циклические ВДР, то интервал берётся равным или кратным циклу. Для того, чтобы не пропадали крайние точки, используют сглаживающие формулы: при
Для крайних значений:
при
Для крайних значений:
Экспоненциальные средние Основа: чем ближе переменная находится к расчётной точке, тем сильнее она должна на неё влиять.
где Средняя формируется под влиянием всех предыдущих значений, но вес каждого из них с каждым шагом уменьшается в
Прогнозирование Для прогнозирования можно использовать методы, рассмотренные нами для сглаживания. 1. Метод скользящего среднего для прогнозирования значений, выходящих за ВДР из
2. Метод взвешенного скользящего среднего
3. Экспоненциальное прогнозирование
. .
4. Метод Бокса-Дженкинса (процедура ARIMA) (АРПСС). Зависимость прогнозируемых значений рассматривается в виде составляющей из двух переменных. AR – авторегрессионный процесс – т. е. зависимость MA – как скользящее среднее текущего и предыдущих значений случайных членов. ARIMA
ARIMA по Боровикову В.
лать заключение о его успешном функционировании.
Методология моделирования Для получения математических моделей можно использовать пассивный или активный эксперименты. Пассивный эксперимент сводится только к наблюдениям за протеканием процесса в объекте исследования и регистрации его характеристик. Активный эксперимент допускает вмешательство в ход процесса и соответственно с этим организацию наблюдений. Моделирование можно рассматривать как процесс, состоящий из искусства и науки, который основывается на основном принципе диалектического познания природы: «от простого созерцания к абстрактному мышлению и от него к практике». Математический аппарат моделирования основывается на теории вероятностей и математической статистики. Достоверность результатов моделирования обеспечивается соблюдением технологии модел
|
||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.017 с.) |

 В формуле оценка математического ожидания произведения переменных х и у вычисляется по формуле:
В формуле оценка математического ожидания произведения переменных х и у вычисляется по формуле: Если коэффициент линейной корреляции близок к 1, то корреляционная связь между переменными положительная, близкая к линейной Если коэффициент линейной корреляции близок к -1, то корреляционная связь между переменными отрицательная, близкая к линейной (рис.16.2). Если коэффициент линейной корреляции близок к 0, то между переменными имеется слабая корреляционная связь (рис.16.3). Для независимых переменных коэффициент линейной корреляции равен нулю.
Если коэффициент линейной корреляции близок к 1, то корреляционная связь между переменными положительная, близкая к линейной Если коэффициент линейной корреляции близок к -1, то корреляционная связь между переменными отрицательная, близкая к линейной (рис.16.2). Если коэффициент линейной корреляции близок к 0, то между переменными имеется слабая корреляционная связь (рис.16.3). Для независимых переменных коэффициент линейной корреляции равен нулю.


 По статистическим таблицам находим критическое значение коэффициента линейной корреляции.
По статистическим таблицам находим критическое значение коэффициента линейной корреляции. В случае, если значение коэффициента линейной корреляции, по абсолютной величине не меньше 0,8, то можно ожидать наличие между переменными линейной зависимости и в уравнения регрессии вводить сами факторы в первой степени. Если значение коэффициента линейной корреляции по абсолютной величине лежит в диапазоне от критического значения до 0,8, то в уравнения регрессии рекомендуется вводить сравнительно несложные функции от факторов. Если значение коэффициента линейной корреляции по абсолютному значению меньше критического, то такие факторы рекомендуется не включать в уравнения регрессии.
В случае, если значение коэффициента линейной корреляции, по абсолютной величине не меньше 0,8, то можно ожидать наличие между переменными линейной зависимости и в уравнения регрессии вводить сами факторы в первой степени. Если значение коэффициента линейной корреляции по абсолютной величине лежит в диапазоне от критического значения до 0,8, то в уравнения регрессии рекомендуется вводить сравнительно несложные функции от факторов. Если значение коэффициента линейной корреляции по абсолютному значению меньше критического, то такие факторы рекомендуется не включать в уравнения регрессии. Функция плотности равномерного закона определяется зависимостью:
Функция плотности равномерного закона определяется зависимостью: при 0£ х£ 1. Для оценки равномерности по тестам частот весь диапазон существования распределения от 0 до 1 разбивают на L интервалов одинаковой длины и подсчитывают попадание случайной величины в каждый из них.
при 0£ х£ 1. Для оценки равномерности по тестам частот весь диапазон существования распределения от 0 до 1 разбивают на L интервалов одинаковой длины и подсчитывают попадание случайной величины в каждый из них. 
 По вычисленным значениям c2 и R по статистическим таблицам находим коэффициент доверия гипотезе о равномерности по КС Пирсона, который должен попасть в 10% интервал 0,1£Рр£0,9. В противном случае гипотеза отвергается.
По вычисленным значениям c2 и R по статистическим таблицам находим коэффициент доверия гипотезе о равномерности по КС Пирсона, который должен попасть в 10% интервал 0,1£Рр£0,9. В противном случае гипотеза отвергается. Два предыдущих случаев дадут отличный результат, если вместо генератора случайных чисел взять обычный счетчик и он будет являться идеально равномерным. Для того чтобы устранить случайность вычисляют коэффициент линейной автокорреляции, показывающий зависимость случайных чисел от ранее сгенерированных. Коэффициент автокорреляции вычисляется для последовательности случайных чисел берущихся с некоторым шагом между собой h.
Два предыдущих случаев дадут отличный результат, если вместо генератора случайных чисел взять обычный счетчик и он будет являться идеально равномерным. Для того чтобы устранить случайность вычисляют коэффициент линейной автокорреляции, показывающий зависимость случайных чисел от ранее сгенерированных. Коэффициент автокорреляции вычисляется для последовательности случайных чисел берущихся с некоторым шагом между собой h. , то такая автокорреляционная связь считается близкой к линейной.
, то такая автокорреляционная связь считается близкой к линейной. 

 Для моделирования требуется использовать генераторы случайных чисел, для которых коэффициент автокорреляции не превышает rкрит, а еще лучше не превышает 0,2 по абсолютной величине.
Для моделирования требуется использовать генераторы случайных чисел, для которых коэффициент автокорреляции не превышает rкрит, а еще лучше не превышает 0,2 по абсолютной величине.




 Факторы.. Отклики.
Факторы.. Отклики.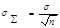 В некоторых случаях, если факторы независимы друг от друга, можно значительно уменьшить количество проводимых экспериметов, применяя план дробных факторных экспериментов (ДФЭ). В ДФЭ факторы разделяются на основные и дополнительные. Для основных факторов составляется план ПФЭ, а дополнительные меняются по законам изменения произведений основных факторов. Таким образом, например, если в эксперименте используется семь факторов, то по плану ПФЭ нам понадобилось бы провести 128 экспериментов. Если же они независимы друг от друга, то выделив из них три основных фактора и составив для них план ПФЭ мы сможем ограничиться всего 9 экспериментами с учётом центральной точки. Планы ДФЭ сохраняют все вышеназванные достоинства планов ПФЭ
В некоторых случаях, если факторы независимы друг от друга, можно значительно уменьшить количество проводимых экспериметов, применяя план дробных факторных экспериментов (ДФЭ). В ДФЭ факторы разделяются на основные и дополнительные. Для основных факторов составляется план ПФЭ, а дополнительные меняются по законам изменения произведений основных факторов. Таким образом, например, если в эксперименте используется семь факторов, то по плану ПФЭ нам понадобилось бы провести 128 экспериментов. Если же они независимы друг от друга, то выделив из них три основных фактора и составив для них план ПФЭ мы сможем ограничиться всего 9 экспериментами с учётом центральной точки. Планы ДФЭ сохраняют все вышеназванные достоинства планов ПФЭ Составим матрицу планирования РЦКП для двух факторов:
Составим матрицу планирования РЦКП для двух факторов:
 =0.148.
=0.148. =0.078.
=0.078. =0.096.
=0.096.

 =0.1458.
=0.1458. =0.08015.
=0.08015. =0.0962.
=0.0962.

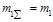 , а. Поэтому для оценок математических ожиданий, вычисляемых на основе суммирования случайных чисел, можно построить доверительный интервал по нормальному закону.
, а. Поэтому для оценок математических ожиданий, вычисляемых на основе суммирования случайных чисел, можно построить доверительный интервал по нормальному закону. 
 .
.
 Вероятность попадания случайной величины в доверительный интервал вычисляется при следующих преобразованиях:
Вероятность попадания случайной величины в доверительный интервал вычисляется при следующих преобразованиях:
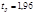 . Задаёмся половиной ширины доверительного интервала
. Задаёмся половиной ширины доверительного интервала  Принимаем
Принимаем 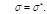 Если условия центральной предельной теоремы теории вероятностей не выполняются, например, если сравнительно невелико количество случайных чисел, или они выработаны при недостаточно общих условиях, например, от весьма различающихся законов или параметров других законов, то применяют неравенство Чебышева:
Если условия центральной предельной теоремы теории вероятностей не выполняются, например, если сравнительно невелико количество случайных чисел, или они выработаны при недостаточно общих условиях, например, от весьма различающихся законов или параметров других законов, то применяют неравенство Чебышева:
 , тогда неравенство (15.13) запишется в виде:
, тогда неравенство (15.13) запишется в виде: 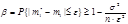 .
.

 , при
, при  ;
; ,при
,при  .
. .
.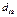 - расстояние между q -ым кластером, к которому подсоединен еще один объект, и g -ым объектом или кластером;
- расстояние между q -ым кластером, к которому подсоединен еще один объект, и g -ым объектом или кластером; - расстояние между i -ым и g -ым объектами или кластерами;
- расстояние между i -ым и g -ым объектами или кластерами; - расстояние между j -ым и g -ым объектами или кластерами;
- расстояние между j -ым и g -ым объектами или кластерами; - расстояние между i -ым и j -ым объектами или кластерами.
- расстояние между i -ым и j -ым объектами или кластерами. равна нулю и корень уравнения
равна нулю и корень уравнения  можно искать приближённо методом касательных, который заключается в построении последовательных приближённых
можно искать приближённо методом касательных, который заключается в построении последовательных приближённых 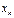 ,
,  следующим образом. В точке
следующим образом. В точке  строится касательная и точка пересечения касательной с осью абсцисс берётся в качестве следующего приближения
строится касательная и точка пересечения касательной с осью абсцисс берётся в качестве следующего приближения


 по формуле продолжают до тех пор, пока не выполнится неравенство
по формуле продолжают до тех пор, пока не выполнится неравенство  , после чего полагают что
, после чего полагают что  .Замечания:
.Замечания: близко к
близко к 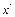 , то метод Ньютона обеспечивает быструю сходимость в поиске экстремума.
, то метод Ньютона обеспечивает быструю сходимость в поиске экстремума. может привести к расходящемуся процессу, т. е. мы будем удаляться от экстремальной точки. Это возможно, если оптимизируемая функция имеет нелинейность выше второй степени.
может привести к расходящемуся процессу, т. е. мы будем удаляться от экстремальной точки. Это возможно, если оптимизируемая функция имеет нелинейность выше второй степени.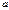 в итерационном процессе произведём следующие преобразования:
в итерационном процессе произведём следующие преобразования:


 и уровнем, принятым за базу сравнения
и уровнем, принятым за базу сравнения 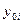 :
:



 на уровень, принятый за базу сравнения:
на уровень, принятый за базу сравнения:
 к предыдущему уровню:
к предыдущему уровню:

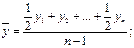
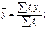



 и правой выборки
и правой выборки  . Примем допущение об однородности дисперсий. Проверка производится по F-критерию Фишера
. Примем допущение об однородности дисперсий. Проверка производится по F-критерию Фишера (где
(где  )
) и
и  ;
; ; если
; если  , то гипотезу не отвергаем. В этом случае можно проводить дальнейшую проверку. Выдвигаем гипотезу о равенстве средних и находим критерий Стьюдента:
, то гипотезу не отвергаем. В этом случае можно проводить дальнейшую проверку. Выдвигаем гипотезу о равенстве средних и находим критерий Стьюдента: ,
,
 находим критическое значение критерия Стьюдента для
находим критическое значение критерия Стьюдента для  количества степеней свободы;
количества степеней свободы; , то гипотеза о равенстве средних отвергается. В этом случае можно проводить прогнозирование.
, то гипотеза о равенстве средних отвергается. В этом случае можно проводить прогнозирование. , где
, где  может меняться как целочисленное значение 1, 2, 3…и расчёт производится для центра интервала:
может меняться как целочисленное значение 1, 2, 3…и расчёт производится для центра интервала:



 ,
,  ;
;


 ,
,  ;
;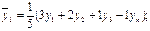 ****
**** ****
****

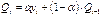 ,
, - коэффициент сглаживания, характеризующий вес текущего наблюдения,
- коэффициент сглаживания, характеризующий вес текущего наблюдения, 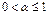 .
. раз, т. е. для расчётного значения это
раз, т. е. для расчётного значения это 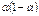 ; затем
; затем  и т. д.…
и т. д.…  …
…

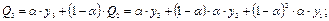

 чисел, например для
чисел, например для 









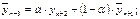

 от своих прошлых значений.
от своих прошлых значений. процесс,
процесс, - порядок MA-части;
- порядок MA-части; - порядок разностей, взятых из исходного ряда для достижения его стационарности.
- порядок разностей, взятых из исходного ряда для достижения его стационарности. - сезонный параметр авторегрессии;
- сезонный параметр авторегрессии; - сезонный параметр скользящего среднего.
- сезонный параметр скользящего среднего.


