
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сглаживание и прогнозирование методом скользящих средних. В чем смысл введения взвешиваний.Содержание книги
Поиск на нашем сайте
Метод скользящего среднего (СС) является наиболее простым из известных методов, он позволяет сгладить периодические и случайные колебания в ВДР и тем самым выявить наличие имеющейся тенденции его изменения. В центрированном сглаживании данные усредняются слева и справа от выбранной точки. Такой вид сглаживания имеет существенный недостаток: сигнал об изменении тенденции существенно запаздывает во времени. Однако необходимо как можно раньше определить момент изменения тенденции, чему способствует использование нецентрированного СС. В существующих ППП [5,13] для сглаживания и прогнозирования применяется нецентрированное СС. В нецентрированном СС усредненная величина заменяет не центральный член интервала усреднения, а его последний член
где yi – фактическое значение переменной на i -ом интервале времени;
m – интервал усреднения. Для прогнозирования, начиная со значения n+ 1 и по r, спрогнозированные значения вычисляются по формуле
Сводные результаты сглаживания и прогнозирования методом скользящего среднего при изменении интервала сглаживания m приведены в таблице 5.2.1. По результатам таблицы 5.2.1 были сделаны следующие выводы: 1. Изменение фактора сглаживания m: 3, 5, 7, 9 с целью выявления наилучшего значения, обеспечивающего минимальную ошибку прогнозирования, существенных результатов по улучшению достоверности не дало. Для каждого показателя деятельности предприятия наилучшие спрогнозированные значения были получены при различных значениях интервала усреднения.
Сглаживание Суть сглаживания сводится к замене фактических уровней ВДР расчётными, имеющими меньшие колебания, чем исходные данные. На практике наиболее часто используют следующие методы: 1. Скользящих средних 2. Взвешенных скользящих средних 3. Экспоненциальный Метод скользящих средних Выбирается интервал сглаживания – нечётное число
Так как каждый раз мы добавляем 1 новый член и 1 вычитаем, то другая запись в виде скользящей средней:
Три свойства скользящих средних
1. Уменьшение нерегулярности колебаний в ряде 2. Чем больше 3. Смещение сглаженных значений 4. Пропадание начальных и конечных значений ряда (концы таблиц) 5. Если требуется сгладить циклические ВДР, то интервал берётся равным или кратным циклу. Для того, чтобы не пропадали крайние точки, используют сглаживающие формулы: при
Для крайних значений:
при
Для крайних значений:
Взвешенные скользящие средние Для устранения недостатков предыдущего метода по смещению экстремальных значений (пиков) и потере мелких колебаний используют взвешенные скользящие, в которых каждой переменной, участвующей в сглаживании придается удельный вес, соответствующий её положению относительно вычисляемого значения. (Этот вес определяется МНК с требованием, чтобы сумма квадратов отклонений вычисленных значений от исходных была минимальной.) ß необязательная фраза. для
для
Сглаживание и прогнозирование экспоненциальных средних Экспоненциальные средние Основа: чем ближе переменная находится к расчётной точке, тем сильнее она должна на неё влиять.
где Средняя формируется под влиянием всех предыдущих значений, но вес каждого из них с каждым шагом уменьшается в
Прогнозирование Для прогнозирования можно использовать методы, рассмотренные нами для сглаживания. 1. Метод скользящего среднего для прогнозирования значений, выходящих за ВДР из
2. Метод взвешенного скользящего среднего
3. Экспоненциальное прогнозирование
. .
4. Метод Бокса-Дженкинса (процедура ARIMA) (АРПСС). Зависимость прогнозируемых значений рассматривается в виде составляющей из двух переменных. AR – авторегрессионный процесс – т. е. зависимость MA – как скользящее среднее текущего и предыдущих значений случайных членов. ARIMA
ARIMA по Боровикову В.
лать заключение о его успешном функционировании.
|
||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.103.114 (0.01 с.) |


 ,
, - сглаженное, или спрогнозированное значение переменной на j -ом интервале времени;
- сглаженное, или спрогнозированное значение переменной на j -ом интервале времени;
 .
. , где
, где  может меняться как целочисленное значение 1, 2, 3…и расчёт производится для центра интервала:
может меняться как целочисленное значение 1, 2, 3…и расчёт производится для центра интервала:



 ,
,  ;
;


 ,
,  ;
;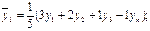 ****
**** ****
****


 :
:
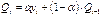 ,
, - коэффициент сглаживания, характеризующий вес текущего наблюдения,
- коэффициент сглаживания, характеризующий вес текущего наблюдения, 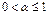 .
. раз, т. е. для расчётного значения это
раз, т. е. для расчётного значения это 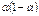 ; затем
; затем  и т. д.…
и т. д.…  …
…

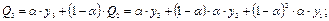

 чисел, например для
чисел, например для 









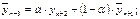

 от своих прошлых значений.
от своих прошлых значений. процесс,
процесс, - порядок MA-части;
- порядок MA-части; - порядок разностей, взятых из исходного ряда для достижения его стационарности.
- порядок разностей, взятых из исходного ряда для достижения его стационарности. - сезонный параметр авторегрессии;
- сезонный параметр авторегрессии; - сезонный параметр скользящего среднего.
- сезонный параметр скользящего среднего.


