Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Табличный метод генерации случайных чисел. Достоинства и недостатки.Содержание книги
Поиск на нашем сайте Табличный метод основан на том же принципе, что и аналитический, только вместо функции распределения в нём берется ее кусочно-линейное представление, то есть весь диапазон существования распределения случайных чисел разбивается на ряд интервалов, в которых дуги заменяются стягивающими их хордами.
ai-1 £rj £ai. На основании подобия треугольников:
Достоинства и недостатки: 1.Реализуются сравнительно несложными программными процедурами. 2.Табличные методы начинают терять свои позиции и в частности из-за того, что для их применения требуется составление таблиц и выделение памяти для их хранения. В принципе повышение достоверности табличных методов можно достичь увеличением количества интервалов в таблице, но при этом увеличивается время поиска нужного интервала и требуемый объем памяти для хранения таблиц.
9. План ПФЭ (полного факторного эксперимента). В графическом виде план проведения эксперимента представляет собой вершины квадрата, как это изображено на рис.15.2.
Вершины квадрата – план полного факторного эксперимента (ПФЭ). Обычно к этим точкам добавляется центральная точка и пять проводимых экспериментов позволяют вычислить четыре коэффициента двухфакторной математической зависимости: y = b0+b1x1+b2x2+b12x1x2. Этот же план можно представить в виде таблицы. Для обеспечения вычислений по одному и тому же алгоритму для всех коэффициентов к свободному члену полинома добавляется так называемый фиктивный фактор х0, который всегда равен единице.
План полного факторного эксперимента (ПФЭ) позволяет вычислить все коэффициенты степенного полинома, включая коэффициенты как при самих факторах, так и при всех сочетаний факторов между собой в виде их произведений. Достоинства плана ПФЭ. 1. Симметричность. Каждая точка плана имеет симметричные себе точки относительно осей координат. В математическом плане симметричность сводится к тому, что построчная сумма элементов всех столбцов плана, кроме левого, равна нулю. 2. Нормированность, которая в математическом плане сводится к тому, что построчная сумма квадратов элементов всех столбцов плана, кроме левого, равна 3. Ортогональность, которая заключается в независимости всех факторов друг от друга. Кроме того следует отметить сравнительную простоту составления плана ПФЭ, который представляет собой полный перебор совокупностей всех факторов по двум уровням. Таким образом, количество точек плана
Планы ПФЭ имеет существенный недостаток, проявляющийся при сравнительно большом количестве факторов, так при K=3, N=8; при K=7, N=128, а при K=10, N=1024, что является неприемлемым. 10. План ОЦКП (ортогональный центральный композиционный план). ОЦКП сохраняет свойство симметричности плана за счёт того, что на каждый фактор вводят по две симметричные звёздные точки. ОЦКП сравнительно несложно построить. ОЦКП в значительной мере упрощает вычисления, что особенно существенно для «ручных» вычислений. Свойство нормированности в ОЦКП сохранить не удаётся, но это и не так важно. Для обеспечения ортогональности столбцов матрицы планирования вводят некоторые сравнительно несложные преобразования. Расстояние звёздной точки от середины осей координат вычисляется по формуле:
Вычисляется вспомогательный коэффициент:
11. Регрессионный анализ с примером для линейной зависимости y=b0+b1x. Регрессионный анализ основан на методе наименьших квадратов, который требует, чтобы сумма квадратов отклонений экспериментальных значений от вычисленных по аппроксимирующей зависимости была минимальной:
Приведём запись уравнения в матричном виде и проведём его преобразование для получения формулы для вычисления коэффициентов полинома.
Составим матрицы X, В, Y и запишем:
После несложных преобразований систем уравнений получим расчётные формулы для вычисления коэффициентов элементов матрицы А.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.007 с.) |


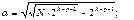 Интервал, в который попало случайное число, определяется по выполнению неравенства
Интервал, в который попало случайное число, определяется по выполнению неравенства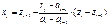 .
.
 .
. ПФЭ N=
ПФЭ N=  . Отметим, что добавляемая к ним центральная точка не является точкой плана ПФЭ. Матрица планирования ПФЭ для двух факторов представляется в следующем виде:
. Отметим, что добавляемая к ним центральная точка не является точкой плана ПФЭ. Матрица планирования ПФЭ для двух факторов представляется в следующем виде:
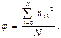
 Вычисляются новые значения элементов столбцов квадратов факторов:
Вычисляются новые значения элементов столбцов квадратов факторов: . В лучшем случае при обработке результатов экспериментов нам известен вид математической зависимости между переменными и тогда следует вычислить только неизвестные коэффициенты. Чаще всего вид математической зависимости неизвестен. В этом случае рекомендуется использовать степенные полиномы, которые при повышении степени полинома позволяют получать аппроксимирующие зависимости с любой заданной точностью.
. В лучшем случае при обработке результатов экспериментов нам известен вид математической зависимости между переменными и тогда следует вычислить только неизвестные коэффициенты. Чаще всего вид математической зависимости неизвестен. В этом случае рекомендуется использовать степенные полиномы, которые при повышении степени полинома позволяют получать аппроксимирующие зависимости с любой заданной точностью.
 Рассмотрим самый простой пример однофакторной зависимости
Рассмотрим самый простой пример однофакторной зависимости  и проведём аппроксимацию этой зависимости линейной функцией:
и проведём аппроксимацию этой зависимости линейной функцией: Пусть проведено n экспериментов, по результатам которых получены n значений Х и n значений Y. Чтобы для вычисления коэффициентов b0 и b1 использовать один и тот же алгоритм введём в (16.7) фиктивную переменную x0, всегда равную 1:
Пусть проведено n экспериментов, по результатам которых получены n значений Х и n значений Y. Чтобы для вычисления коэффициентов b0 и b1 использовать один и тот же алгоритм введём в (16.7) фиктивную переменную x0, всегда равную 1: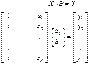
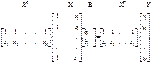 Проведём несложные матричные преобразования и получим формулы для вычисления коэффициентов полинома:
Проведём несложные матричные преобразования и получим формулы для вычисления коэффициентов полинома:

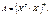 Требуется провести обращение матрицы
Требуется провести обращение матрицы 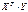 , т. е. получить матрицу
, т. е. получить матрицу Умножение обратной и «своей» прямой матрицы даёт в произведении единичную матрицу, в которой элементы главной диагонали равны единице, а остальные элементы равны нулю.
Умножение обратной и «своей» прямой матрицы даёт в произведении единичную матрицу, в которой элементы главной диагонали равны единице, а остальные элементы равны нулю.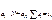





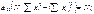




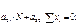
 Запишем окончательный результат:
Запишем окончательный результат: