
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение дисперсионного анализа для оценки качества уравнений регрессии. Оценка значимости коэффициентов полинома.Содержание книги
Поиск на нашем сайте
Дисперсионный анализ основан на разложении общей изменчивости результативного показателя на объяснённую дисперсию, которую удалось объяснить изменением переменных, вошедших в уравнение регрессии, и остаточную регрессию, которую объяснить не удалось. Для проведения дисперсионного анализа вычисляются. 1. Объяснённая сумма квадратов:
с количеством степеней свободы:
среднее значение суммы квадратов:
2. Остаточная сумма квадратов:
среднее значение суммы квадратов:
3.
с количеством степеней свободы: Должно выполняться равенство:
4. Критерий Фишера
с количеством степеней свободы:
5.
с количеством степеней свободы: Показывает, какую часть изменения результативного показателя удалось объяснить изменением переменных, вошедших в уравнение регрессии. Если вычисленные значения не меньше критических значений, то результаты аппроксимации признаются удовлетворительными. 6.
чем больше величина
Вычисляем критическое значение критерия Стьюдента
Метод оптимизации по системе ур-й в частных производных. Постановка задачи оптимизации в общем случае сводится к максимизации или минимизации целевой функции с ограничениями на остальные функции и оптимизируемые факторы:
…
Наиболее простой случай, когда нет никаких ограничений. В этом случае применяется классический метод вычисления по решению системы в частных производных по оптимизируемым переменным.
Рассмотрим двухфакторную математическую зависимость:
Вид экстремума определяется значением вторых частных производных:
1. Если 2. Если 3. Если 4. Если Рассмотрим частный случай двухфакторной функции:
Вычислим частные производные и координаты экстремальной точки:
Геометрический метод для 2 факторов. Если требуется найти оптимальные значения всего двух факторов, то можно использовать геометрический метод оптимизации, отличающийся сравнительной простотой и наглядностью.
Приравняем целевую функцию нулю и выразим все переменные через одну из них. Представим преобразованные ограничения и целевую функцию в виде прямых линий. Построим область допустимых решений (ОДР). Первая точка пересечения линии целевой функции с ОДР является точкой минимума; последняя – максимума. Проверим выполнение неравенств в точках min (max). Если все неравенства выполняются делаем заключение о корректности полученных результатов.
Метод Ньютона. Для решения оптимизационных задач с нелинейными функциями можно использовать метод Ньютона (метод касательных). Метод Ньютона требует, чтобы оптимизируемая функция была дважды дифференцируема. В экстремальной точке производная функции
,
Вычисления 1. Если начальное приближение 2. Если начальное приближение Для вычисления шага изменения значения аргумента
1. Временные динамические ряды. основные понятия. проверка гипотез о существовании тенденций. Временные ряды Временными динамическими рядами (ВДР) называются статистические данные, отображающие развитие изучаемого процесса (явления) во времени. В качестве фактора в ВДР используются либо даты, либо интервалы времени. В качестве отклика – количественные показатели развития изучаемого процесса во времени. Основная цель статистического изучения временных динамических рядов (ВДР) состоит в выявлении и оценивании закономерностей их развития. Основные показатели динамики ВДР 1. Базисный абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
2. Цепной абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем
3. Базисный темп роста, вычисляется делением сравниваемого уровня на уровень, принятый за базу:
4. Цепной темп роста, вычисляется делением сравниваемого уровня на предыдущий:
5. Базисный темп прироста – вычисляется делением базисного абсолютного прироста
6. Цепной темп прироста – вычисляется как отношение сравниваемого цепного абсолютного прироста
7. Средний уровень ВДР (оценка математического ожидания): § для интервального ряда:
§ для моментного ряда с равностоящими датами:
§ для момента ряда с неравностоящими датами:
8. Средний абсолютный прирост:
9. Средний темп роста:
10. Средний темп прироста:
Проверка гипотезы о существовании тенденции Проверка разности средних уровней: Разбиваем анализируемый ряд на две примерно одинаковые выборки, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность. Принимаем допущение, что выделенные выборки подчиняются нормальному закону (можно проверить в ППП Statistica). Воспользуемся методикой, разработанной для малых выборок. Находим средние значения для левой выборки
число степеней свободы Принимаем уровень значимости по рекомендации
где S – среднее квадратическое отклонение разности средних.
При уровне значимости Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |



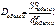

 с количеством степеней свободы:
с количеством степеней свободы:
 Общая сумма квадратов:
Общая сумма квадратов:
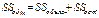



 Коэффициент множественной детерминации,
Коэффициент множественной детерминации,

 Так как коэффициенты уравнения регрессии вычисляются по случайным величинам, то они и сами являются случайными величинами. Поэтому можно вычислить их стандартные ошибки и по ним определить критерий Стьюдента и уровни их значимости.
Так как коэффициенты уравнения регрессии вычисляются по случайным величинам, то они и сами являются случайными величинами. Поэтому можно вычислить их стандартные ошибки и по ним определить критерий Стьюдента и уровни их значимости. где
где  -диагональный элемент матрицы.
-диагональный элемент матрицы. , тем лучше.
, тем лучше. . Если вычисленное значение
. Если вычисленное значение  превышает критическое, то считаем, что уровень значимости
превышает критическое, то считаем, что уровень значимости  не превышает рекомендуемого значения
не превышает рекомендуемого значения  , и поэтому вычисленные значения коэффициентов приемлемы для отображения экспериментальных данных. В противном случае рекомендуется подобрать другие значения переменных в аппроксимирующее уравнение регрессии, в виде каких-либо функций от аргументов.
, и поэтому вычисленные значения коэффициентов приемлемы для отображения экспериментальных данных. В противном случае рекомендуется подобрать другие значения переменных в аппроксимирующее уравнение регрессии, в виде каких-либо функций от аргументов.

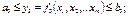









 и
и 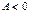 , то имеем максимум.
, то имеем максимум. и
и  , то имеем минимум.
, то имеем минимум. то нет ни мин, ни макс.
то нет ни мин, ни макс. , то экстремум может быть или не быть. Требуется дополнительное исследование.
, то экстремум может быть или не быть. Требуется дополнительное исследование.


 Постановка задачи оптимизации:
Постановка задачи оптимизации: равна нулю и корень уравнения
равна нулю и корень уравнения  можно искать приближённо методом касательных, который заключается в построении последовательных приближённых
можно искать приближённо методом касательных, который заключается в построении последовательных приближённых 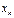 ,
,  следующим образом. В точке
следующим образом. В точке  строится касательная и точка пересечения касательной с осью абсцисс берётся в качестве следующего приближения
строится касательная и точка пересечения касательной с осью абсцисс берётся в качестве следующего приближения


 по формуле продолжают до тех пор, пока не выполнится неравенство
по формуле продолжают до тех пор, пока не выполнится неравенство  , после чего полагают что
, после чего полагают что  .Замечания:
.Замечания: близко к
близко к 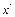 , то метод Ньютона обеспечивает быструю сходимость в поиске экстремума.
, то метод Ньютона обеспечивает быструю сходимость в поиске экстремума. может привести к расходящемуся процессу, т. е. мы будем удаляться от экстремальной точки. Это возможно, если оптимизируемая функция имеет нелинейность выше второй степени.
может привести к расходящемуся процессу, т. е. мы будем удаляться от экстремальной точки. Это возможно, если оптимизируемая функция имеет нелинейность выше второй степени.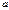 в итерационном процессе произведём следующие преобразования:
в итерационном процессе произведём следующие преобразования:


 и уровнем, принятым за базу сравнения
и уровнем, принятым за базу сравнения 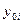 :
:



 на уровень, принятый за базу сравнения:
на уровень, принятый за базу сравнения:
 к предыдущему уровню:
к предыдущему уровню:

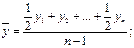
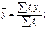



 и правой выборки
и правой выборки  . Примем допущение об однородности дисперсий. Проверка производится по F-критерию Фишера
. Примем допущение об однородности дисперсий. Проверка производится по F-критерию Фишера (где
(где  )
) и
и  ;
; ; если
; если  , то гипотезу не отвергаем. В этом случае можно проводить дальнейшую проверку. Выдвигаем гипотезу о равенстве средних и находим критерий Стьюдента:
, то гипотезу не отвергаем. В этом случае можно проводить дальнейшую проверку. Выдвигаем гипотезу о равенстве средних и находим критерий Стьюдента: ,
,
 находим критическое значение критерия Стьюдента для
находим критическое значение критерия Стьюдента для  количества степеней свободы;
количества степеней свободы; , то гипотеза о равенстве средних отвергается. В этом случае можно проводить прогнозирование.
, то гипотеза о равенстве средних отвергается. В этом случае можно проводить прогнозирование.


