
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Группировка. общие понятия. постановка задачи и технология проведения кластерного анализа.Содержание книги
Поиск на нашем сайте
Группировки В общем случае при статистических исследованиях может рассматри-ваться к объектов, каждый из которых может характеризоваться l признака-ми по n интервалам времени. Для корректного применения основного метода статистических исследований – регрессионного анализа, обладающего срав-нительной простотой и конструктивностью, рекомендуется обеспечить одно-родность исследуемых вероятностных объектов по всем трём вышеназван-ным показателям, т. е. по объектам, по признакам и по временным интерва-лам. Для группировки объектов используется кластерный анализ, для групп-пировки признаков – факторный и компонентный анализ, для группировки временных интервалов−периодизация. В любом случае при группировке до-биваются, чтобы различия внутри выделенных групп были бы минимальны, а между группами максимальны. Невзирая на наличие формализации всех методов группировок все они являются численными методами и их можно отнести к эвристическим методам, основанным на «здравом смысле». Для оценки подобия (однородности) на практике используется три типа мер: коэффициенты подобия, коэффициенты связи, показатели расстояния. 1. Коэффициенты подобия можно применять если уровни признаков могут быть представлены целыми числами. Числа переводятся в двоичную систему и в них подсчитывается количество совпадающих разрядов («0» с «0», «1» с «1»). Например, рассмотрим два объекта, характеризующихся тремя признаками. Исходные данные объектов и результаты вычислений представлены в таблице 19.1.
Таблица 19.1
В таблице 19.1 представлены результаты вычисления наиболее используемого коэффициента подобия по общему количеству совпадений «0» и «1» в двоичных разрядах чисел. Можно учитывать только количество совпадений «1» (коэффициент Рао) 5/21=0,238. Чтобы усилить значимость совпадений можно использовать коэффициент Хаммана (10-11)/21=−0,048 (где 5+5=10 количество совпадений, а 21-10=11 количество несовпадений значений в разрядах). Если в числитель подставить количество совпадений «1» в разрядах чисел, а в знаменатель количество пар хотя бы с одной «1», то можно вычислить коэффициент Роджерса-Танимото) 5/16=0,3125. 2. Коэффициенты связи, как правило, применяются для группировки признаков. В качестве коэффициента связи чаще всего используется коэф- фициент линейной корреляции, а для проведения группировки квадратная матрица коэффициентов линейной корреляции между признаками. 3. В качестве показателей расстояния используют: -расстояние Евклида; -расстояние Хемминга; -расстояние Маханолобиса.
Кластерный анализ Поставим задачу выделения кластеров по показателям расстояния между признаками в группируемых ОИ с выполнением следующих условий.
где k – количество объектов;
Признаки представляются либо в натуральных единицах измерения, либо в стандартизированной форме, в которой их средние значения равны нулю, а стандартные отклонения равны единице. В стандартных процедурах для проведения кластерного анализа, как правило задается либо количество кластеров, либо пороговое значение для условия (19.1). Условие (19.1) обеспечивает минимум расстояний между признаками объектов, вошедших в один и тот же кластер; а (19.2) максимум этих расстояний между объектами, вошедшими в разные кластеры. Технология применения кластерного анализа включает в себя следующие этапы: 1. Стандартизация исходных статистических данных выполняется в случаях, когда учитываемые признаки имеют различные единицы измерения или значительно отличаются по масштабам единиц измерения. 2. Вычисление расстояний между признаками объектов и суммарного расстояния между объектами по всем признакам и составление матрицы расстояний между объектами. 3. Поиск наименьшего расстояния между объектами и объединение двух объектов с наименьшим расстоянием между ними в один кластер. 4. Вычисление расстояний между объектами и формирующимися кластерами и преобразование матрицы расстояний между ними. Переход к пункту 3 и выполнение пунктов 3 и 4 до тех пор, пока не будут сгруппированы все объекты и сформированные кластеры в один общий кластер, после чего переход к пункту 5. 5. Выдача перечней объектов по выделенным кластерам в виде таблицы и соответствующей дендрограммыс указанием расстояний между объектами в выделенных кластерах и сформированными кластерами. Расстояние между объектами по Евклиду вычисляется по формуле:
по Хеммингу:
где dij − расстояние между i- ым и j- ым объектами; k – количество объектов; l – количество признаков; xig – значение i- го признака g- го объекта; xjg −значение j- го признака g- го объекта. Расстояние от формирующегося кластера с вошедшими в него объектами до других объектов может вычисляться по следующим правилам. 1. Принцип ближайшего соседа.
2. Принцип наиболее удаленного соседа.
3.Принцип среднего расстояния.
3. Принцип медианы.
В формулах (19.5) - (19.8) приняты следующие обозначения:
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.213.204 (0.009 с.) |


 ,
, - расстояние между i -м и j -м объектами;
- расстояние между i -м и j -м объектами;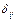 - символ Кронекера, принимающий значение 1, если i -ый и j -ый объекты входят в один и тот же кластер; и значение 0, если не входят.
- символ Кронекера, принимающий значение 1, если i -ый и j -ый объекты входят в один и тот же кластер; и значение 0, если не входят. ; (19.3)
; (19.3) ;
;  ;
; 
 , при
, при  ;
; ,при
,при  .
. ;
; ,при
,при  .
. .
. .
. - расстояние между q -ым кластером, к которому подсоединен еще один объект, и g -ым объектом или кластером;
- расстояние между q -ым кластером, к которому подсоединен еще один объект, и g -ым объектом или кластером; - расстояние между i -ым и g -ым объектами или кластерами;
- расстояние между i -ым и g -ым объектами или кластерами; - расстояние между j -ым и g -ым объектами или кластерами;
- расстояние между j -ым и g -ым объектами или кластерами; - расстояние между i -ым и j -ым объектами или кластерами.
- расстояние между i -ым и j -ым объектами или кластерами.


