
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл предела функции в точкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Дан график функции 2. Неравенство 3. Неравенство не выходят за интервал 4. Если выполняется равенство
Рис.2.
Эквивалентность двух определений Предела функции в точке Теорема №2. Первое и второе определение предела функции в данной точке эквивалентны. Доказательство I. 1. Пусть 2. Предположим обратное, что число 3. Это значит, что не для любого 4. Возьмём в качестве 5. Тогда для
Для Для ………………………………………………………………………… Для ………………………………………………………………………… 6. В результате получается последовательность точек, отличных от 7. Тогда согласно первому определению предела функции в точке по Гей не, соответствующая последовательность 8. Следовательно, по определению предела последовательности 9. А по принятому (п.5) должно выполняться неравенство 10. Полученное противоречие и доказывает, что число II. 1. Пусть дано, что число 2. Если число 3. Возьмём любую последовательность точек 4. Тогда согласно определения предела последовательности 5. Вместе с тем в силу второго определения предела функции в точке будет выполняться и 6. Так как 7. Таким образом, число Замечание №2 1. Итак, установлена эквивалентность обоих опре- делений предела функции в точке. Можно использовать любое из них в зависимости от того, какое более удобно при решении той или иной задачи. 2. Оба определения сами по себе еще не дают способа отыскания предела данной функции в точке. С их помощью иногда можно установить, будет ли то или иное число пределом функции, или можно убедиться, что данная функция вовсе не имеет предела [15]. Односторонние пределы
1. Кроме рассмотренного предела функции в точке существует такое понятие как предел в точке слева или предел в точке справа. Определение №3. Число Символически: Определение №4. Число Символически: Иными словами: Если бы в определении предела функции в точке потребовалось бы, чтобы х стремился к Аналогично, если существует предел функции Определение №5. Пределы слева и справа функции в точке называются односторонними в отличие от предела функции в точке, который называется двусторонним. Теперь рассмотрим равносильные определения односторонних пределов функции в точке слева и справа «на языке Определение №6. Число Символически:
Графически:
Рис.3. Определение №7 («на языке
Символически: Графически:
Рис.4.
Пример 5. Функция а) б)
Рис.5. Замечание №3. Не пишут
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.199 (0.006 с.) |

 .
. означает, что
означает, что  отстоит от
отстоит от  не далее, чем на
не далее, чем на 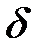 . Т. е.
. Т. е. 

 или «говорят» принадлежит проколотой
или «говорят» принадлежит проколотой  - окрестности точки
- окрестности точки  оси Ох:
оси Ох:  [24].
[24].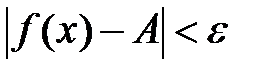 означает, что значения функции
означает, что значения функции 
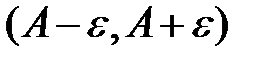 оси ординат. Т. е. значения функции
оси ординат. Т. е. значения функции 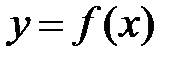 принадлежат
принадлежат  - окрестности точки
- окрестности точки  оси Оy:
оси Оy: 
 .
. , то точка
, то точка  должна находиться в полосе шириной
должна находиться в полосе шириной  , ограниченной прямыми
, ограниченной прямыми  ,
,  , для всех значений х, удаленных от точки
, для всех значений х, удаленных от точки  [2].
[2].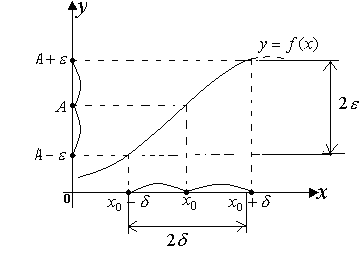
 – предел функции f(x) в точке
– предел функции f(x) в точке  согласно первому определению предела функции в точке. Требуется доказать, что число
согласно первому определению предела функции в точке. Требуется доказать, что число 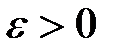 можно указать такое
можно указать такое  , что из неравенства
, что из неравенства  следовало бы неравенство
следовало бы неравенство  . Т. е., сущест- вует такое
. Т. е., сущест- вует такое 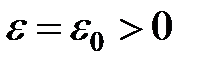 , для которого какое бы
, для которого какое бы 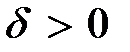 ни взять, найдётся хоть одна точка
ни взять, найдётся хоть одна точка  такая, что
такая, что  , но
, но  .
.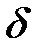 последовательно такие числа:
последовательно такие числа: 
 во множестве X найдётся такая точка
во множестве X найдётся такая точка  что
что , а
, а 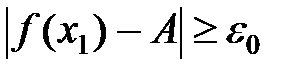 .
. во множестве X найдётся такая точка
во множестве X найдётся такая точка  что
что  , а
, а  ;
; во множестве X найдётся такая точка
во множестве X найдётся такая точка  что
что  ,а
,а  ;
; во множестве X найдётся такая точка
во множестве X найдётся такая точка  , а
, а 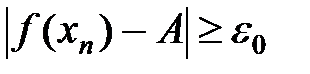 .
.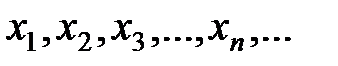 , сходящаяся к
, сходящаяся к  стремится к нулю при
стремится к нулю при  (
( .
. значений функции схо- дится к числу
значений функции схо- дится к числу 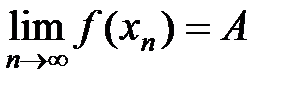 [2].
[2]. найдется такой номер
найдется такой номер  , что для всех
, что для всех  будет выполнятся
будет выполнятся  .
. в точке
в точке 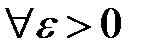 существует такое
существует такое  , что из неравенства
, что из неравенства  следует неравенство
следует неравенство 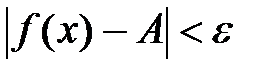 .
. :
:  , схо- дящуюся к точке
, схо- дящуюся к точке 
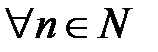 .
.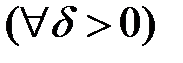
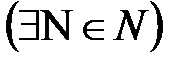
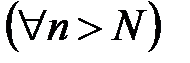 будет выполняться неравенство
будет выполняться неравенство  .
.
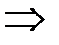
 ,
,  выбиралось произвольно, последовательность точек
выбиралось произвольно, последовательность точек 
 называется правым пределом (или пределом справа) функции
называется правым пределом (или пределом справа) функции  в точке
в точке  , все элементы которой больше
, все элементы которой больше  сходится к
сходится к  или
или  или
или  .
. в точке
в точке  , если для любой, сходящейся к
, если для любой, сходящейся к  , все элементы которой меньше
, все элементы которой меньше  сходится к
сходится к  или
или  или
или  .
. ».
». существует такое
существует такое 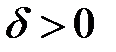 , что для всех х, удовлетворяющих неравенствам
, что для всех х, удовлетворяющих неравенствам 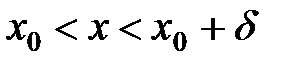 , выполняется неравенство
, выполняется неравенство 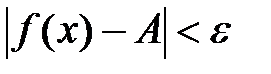




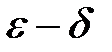 »). Число
»). Число  , если
, если
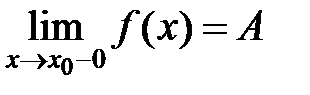 .
.

 (сигнум) имеет в точке
(сигнум) имеет в точке  левый и правый пределы функции в точке (рис. 5).
левый и правый пределы функции в точке (рис. 5).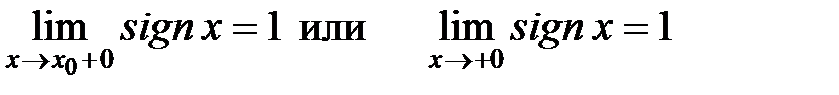
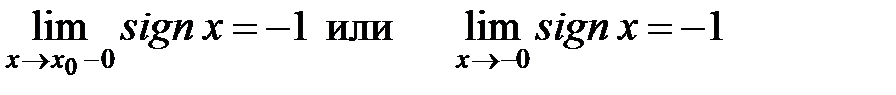

 , а пишут
, а пишут  .
. , а пишут
, а пишут  [2].
[2].


