
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление действительного числа бесконечной
Десятичной дробью Лемма: Каково бы ни было действительное число Доказательство: 1.Пусть задано некоторое действительное число 2.В силу аксиомы Архимеда: «Каково бы ни было число, существует такое натуральное число 3.Среди натуральных чисел 4.Так как Покажем на рисунке.
5.Обозначим отрезок
6.Рассмотрим последовательность отрезков 1ый отрезок будет 2ой отрезок будет ……………………………………………………… 10ый отрезок будет 7.Для точки а) либо точка
б) либо точка
или
8.В случае а) точка 9.В другом случае точка 10.Разобьем отрезок 11.Обозначим через 12.Продолжая этот процесс разбиения на отрезок, получим последовательность вложенных отрезков: 13.Каждый из отрезков содержит точку 14.Длина nого отрезка Определение №1: Конечные десятичные дроби Определение №2: Число 15.Сформулируем свойства нижнего и верхнего десятичных приближений порядка nого числа а) последовательность отрезков б) длина nого отрезка в) точка
г) левые концы отрезков д) правых концы отрезков образуют убывающую последовательность
Следовательно, получаем стягивающую последовательность вложенных отрезков
16.Согласно замечанию №1 к теореме (принципу) Коши-Кантора точка
17.Таким образом, лемма доказана. Замечание: Если Следствие к лемме: Всякое действительное число является пределом последовательности рациональных чисел. Следствие теоремы вытекает из того, что Модуль Тема №2 Предел последовательности Лекция №8 1. Число е. 2. Подпоследовательности. 3. Теорема о сходимости подпоследовательности сходящейся последовательности. 4. Теорема Больцано – Вейерштрасса. Число е Докажем, что Доказательство: 1.Рассмотрим последовательность Требуется доказать, что, 2.Известно, что возрастающая последовательность, ограниченная сверху сходится к конечному числу. 3.Воспользуемся формулой бинома Ньютона:
4.Представим выражение в следующем виде:
5.Аналогичным образом представим элемент
6.Сравним два выражения 7.Так как, 8.Сравним Каждое слагаемое в выражении 9.Рассмотрим опять nый элемент последовательности:
10.Каждое выражение, стоящее в круглых скобках меньше 1, т.е.
11.Учитывая это, получим,
12.Известно, что (Например, 13.Поэтому можно записать 14.Но 15.Тогда 16.Итак, последовательность А всякая последовательность, возрастающая и ограниченная сверху (по теореме Вейерштрасса) имеет конечный предел. Как оказалось
Ч.т.д.
Модуль Тема №3
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.032 с.) |
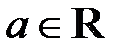 , последовательность
, последовательность 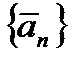 монотонно убывает, последовательность
монотонно убывает, последовательность  монотонно возрастает, и
монотонно возрастает, и  .
. . Для определенности, пусть
. Для определенности, пусть 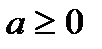 .
. , что,
, что,  : (
: ( ):
):  возьмем такое
возьмем такое  , наименьшее из них и обладающее свойством
, наименьшее из них и обладающее свойством  . Обозначим его
. Обозначим его  , т.е.
, т.е.  .
. . Значит, можно написать
. Значит, можно написать  .
.
 и разобьем его на 10 равных частей.
и разобьем его на 10 равных частей.
 , где
, где  .
.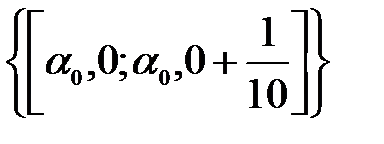 =
=  , когда
, когда 
 .
. =
=  , когда
, когда 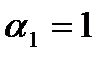
 .
. =
=  , когда
, когда 
 .
.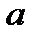 возможны два случая:
возможны два случая:
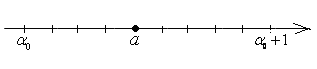

 ;
;  :
:  , где
, где  .
. обозначим из них тот, для которого точка
обозначим из них тот, для которого точка  .
. в свою очередь на десять равных частей, на 10 равных отрезков.
в свою очередь на десять равных частей, на 10 равных отрезков. тот из них, который содержит точку
тот из них, который содержит точку  .
. , где
, где 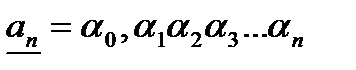 ,
,  (
( ,
,  ).
).
 ,
,  .
.


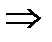
 при
при  .
. называются десятичными дробями, приближающими число
называются десятичными дробями, приближающими число  называется нижним десятичным приближением порядка
называется нижним десятичным приближением порядка  числа
числа  ,
,  образуют последовательность вложенных отрезков
образуют последовательность вложенных отрезков  или
или  ;
;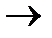 к 0
к 0 
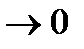 при
при 
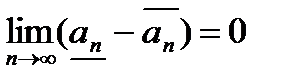 и
и  ;
;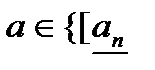 ,
,  при
при  .
. образуют возрастающую последовательность;
образуют возрастающую последовательность; .
.
 ,
,  .
. , то нужно принять
, то нужно принять  и выполнить подобные исследования.
и выполнить подобные исследования. и
и  суть рациональные числа.
суть рациональные числа. .
. с общим членом
с общим членом  :
:  ,
,  , …,
, …,  ,…. (2; 2,25; 2,357; 2,44; …,
,…. (2; 2,25; 2,357; 2,44; …,  ,…).
,…).
 – иррациональное число, т.е., что последовательность
– иррациональное число, т.е., что последовательность  сходится к
сходится к  при
при 
 .
. или
или .
. данной последовательности:
данной последовательности: .
. и
и 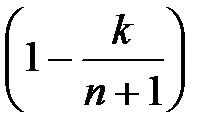 ,
,  .
. , то
, то  поэтому
поэтому  .
. и
и  .
. больше соответствующего слагаемого в выражении
больше соответствующего слагаемого в выражении  . Кроме того, у
. Кроме того, у  , т.е. последовательность
, т.е. последовательность  .
. .
. , так как
, так как
 .
.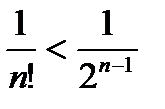 при
при  .
. ;
;  и т.д.).
и т.д.). или
или  .
. это сумма убывающей геометрической прогрессии с
это сумма убывающей геометрической прогрессии с  ;
;  . Следовательно,
. Следовательно,  .
.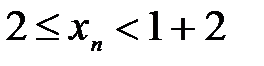 или
или  при
при  .
. возрастает и ограничена сверху 3.
возрастает и ограничена сверху 3. .
.


