
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции по Гейне и КошиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Генрих Эдуард Гейне (1821-1881)– немецкий математик. 1.Пусть дана функция
Таким образом, Теперь можно поставить вопрос о существовании предела функции Определение №1 по Гейне(«на языке последовательностей»). Число Символически это записывается так: Из определения следует, что функция а) б) Примеры. 1). Функция Доказательство 1. Если 2. Значит, предел последовательности значений функции имеет тот же предел: 3. На основании определения предела функции в точке по Гейне функция 4. Так как точка
Рис.1. 2). Функция Доказательство 1. Пусть последовательность значений аргумента, сходящаяся к 2. Тогда последовательность значений функции будет иметь вид:
3. Т. е. последовательности 4. Значит, последовательность значений функции имеет тот же предел: 5. Поэтому на основании определения предела функции в точке по Гей- не функция 6. Так как точка
3). Функция Дирихле Доказательство 1. Так для последовательности рациональных значений аргумента, схо- дящейся к 2. А для последовательности иррациональных значений аргумента, сходящейся к 3. Следовательно, Огюстен Луи Коши (1789-1857) –французский математик. Определение №2 по Коши («на языке
С помощью символов определение можно записать так:
Замечание №1. Неравенство
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.31.82 (0.006 с.) |

 , определённая на некотором множестве
, определённая на некотором множестве  . И пусть точка
. И пусть точка  или
или  . Возьмём из множества
. Возьмём из множества  отличных от
отличных от  при
при  :
: , сходящуюся к
, сходящуюся к  , т.е.
, т.е.  .
. ., т.е.
., т.е.  [30].
[30]. в точке
в точке  называется пределом функции
называется пределом функции  в точке
в точке  , если для любой сходящейся к
, если для любой сходящейся к  схо- дится к числу
схо- дится к числу  или
или 
 .
. , определенная на множестве Х, имеет предел, равный
, определенная на множестве Х, имеет предел, равный  — сходящаяся к
— сходящаяся к  ,
,  ,
,  .
. — сходящаяся к
— сходящаяся к  .
. . Доказать, что эта функция имеет в каждой точке
. Доказать, что эта функция имеет в каждой точке  числовой прямой предел, равный
числовой прямой предел, равный  .
. будет иметь вид:
будет иметь вид:  или
или 
 .
. будет иметь тот же предел в точке
будет иметь тот же предел в точке  .
.

 . Доказать, что в каждой точке
. Доказать, что в каждой точке  числовой прямой эта функция имеет предел, равный
числовой прямой эта функция имеет предел, равный  .
. 


 ,
, 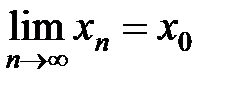 .
. или
или  ,…
,…  .
.
 , т. е.
, т. е.  .
. не имеет предела ни в одной точке
не имеет предела ни в одной точке  предела не имеет [30]. Ч.т.д.
предела не имеет [30]. Ч.т.д. »). Число
»). Число  называется пределом функции
называется пределом функции  в точке
в точке  , если для
, если для 

 выполняется неравенство
выполняется неравенство  .
.
 .
. можно записать так:
можно записать так: .
.


