
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 29. Задача линейного программирования. Экономический анализ задач с использованием теории двойственности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейное программирование — наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений. Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи. В общем виде математическая модель задачи линейного программирования (ЛП) записывается как
…………………………………..
Математическая модель в более краткой записи имеет вид Допустимым решением (планом) задачи линейного программирования называется вектор Х = (x1,…,xn), удовлетворяющий системе ограничений. Множество допустимых решений образует область допустимых решений (ОДР). Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается Хопт. Математическая модель задачи ЛП может быть канонической и неканонической. Если все ограничения системы заданы уравнениями и переменные неотрицательные, то такая модель задачи называется канонической. Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое неравенство ввести балансовую переменную xn+i. Если знак неравенства £, то балансовая переменная вводится со знаком плюс, если знак неравенства ³, то — минус. В целевую функцию балансовые переменные не вводятся. Чтобы составить математическую модель задачи ЛП, необходимо: - ввести обозначения переменных; - исходя из цели экономических исследований, составить целевую функцию; -учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений. Наиболее простым и наглядным методом линейного программирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в неканонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных. С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста. Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор gradL(х) на данной плоскости, который обозначим С. Этот вектор показывает направление наискорейшего изменения целевой функции, он равен Алгоритм решения задач 1. Находим область допустимых решений системы ограничений задачи. 2. Строим вектор С. 3. Проводим линию уровня Lo, которая перпендикулярна С. 4. Линию уровня перемещаем по направлению вектора С для задач на максимум и в направлении, противоположном С, для задач на минимум. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум. Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми. 5. Находим координаты точки экстремума и значение целевой функции в ней. Пример: Выбор оптимального варианта выпуска изделий Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в табл.
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным? решение. Обозначим: x1 — суточный объем выпуска сливочного мороженого, кг; x2 — суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид L(x) = 16 x1 + 14 x2 -> max при ограничениях:
Решая систему, получим координаты точки D(312,5; 300), в которой и будет оптимальное решение, т.е. Х(опт)=(312,5;300), при этом Lmax(x)=16*312,5+14*300=9200р. Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р.
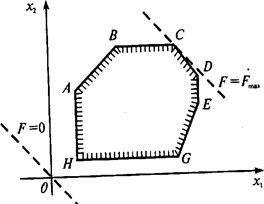
Идея симплексного метода (метода последовательного улучшения плана) заключается в том, что, начиная с некоторого исходного опорного решения, осуществляется последовательно направленное перемещение по опорным решениям задачи к оптимальному. Значение целевой функции при этом перемещении для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оптимальное опорное решение. Опорным решением называется базисное неотрицательное решение. Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому можно предложить такой способ решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограничений и выбрать среди них то, на котором функция цели принимает оптимальное решение. Геометрически это соответствует перебору всех угловых точек многогранника решений. Такой перебор, в конце концов, приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допустимых базисных решений хотя и конечно, но может быть чрезвычайно велико. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или, по крайней мере, "не хуже"), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума F-> max, уменьшение — при отыскании минимума F-> min). Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере. Пусть область допустимых решений изображается многоугольником ABCDEGH. Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем — к оптимальной точке С.
Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию. Рассмотрим две задачи I и II линейного программирования, обладающими следующими свойствами: 1. В одной задаче ищут максимум линейной функции, в другой — минимум. 2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой. 3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "<", а в задаче минимизации — все неравенства вида ">". 4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу. Различают симметричные, несимметричные и смешанные двойственные задачи. Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами. В дальнейшем для простоты будем называть их просто двойственными задачами. Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи. 1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду "≤", а если минимум — к виду "≥". Для этого неравенства, в которых данное требование не выполняется, умножить на -1. 2. Составить расширенную матрицу системы, в которую включить матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции. 3. Найти матрицу, транспонированную к данной матрице. 4. Сформулировать двойственную задачу на основании полученной матрицы и условия неотрицательности переменных. Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. ТЕОРЕМА 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений Х и Y выполняется равенство Если одна из двойственных задач неразрешима ввиду того, что ТЕОРЕМА 2. Для оптимальности допустимых решений Х и У пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой. Пример. Порешению исходной задачи найти решение двойственной, и наоборот. Исходная задача
Двойственная задача будет иметь вид:
Исходную задачу можно решить графически. Получим Х(опт)=(4,1), при этом L(x)=3. На основании первой теоремы двойственности Так как
Тогда система ограничений двойственной задачи примет вид С другой стороны, пусть дано решение двойственной задачи Y(опт)=(0,2/3,1/3), при этом По первой теореме Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле Y(опт)=С*А-1где С – матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи, А-1 –обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы ограничений исходной задачи в оптимальном решении. Двойственные задачи позволяют получить решение исходной задачи, если оно затруднительно или громоздко.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1852; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.008 с.) |

 при ограничениях:
при ограничениях: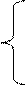

 , где хj — неизвестные; аij, bj, cj — заданные постоянные величины. Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
, где хj — неизвестные; аij, bj, cj — заданные постоянные величины. Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.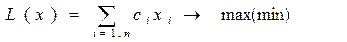 при ограничениях:
при ограничениях: 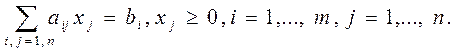
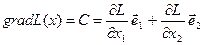 , где е1 и e2 — единичные векторы. Координатами вектора С являются коэффициенты целевой функции L{x).
, где е1 и e2 — единичные векторы. Координатами вектора С являются коэффициенты целевой функции L{x).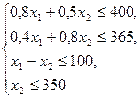
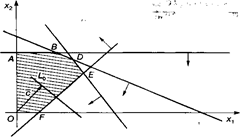 OABDEF — область допустимых решений. Строим вектор с(1,1). Линия уровня задается уравнением 16x1+14x2=const. Перемещаем линию уровня по направлению вектора с. Точкой выхода из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями:
OABDEF — область допустимых решений. Строим вектор с(1,1). Линия уровня задается уравнением 16x1+14x2=const. Перемещаем линию уровня по направлению вектора с. Точкой выхода из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями: 
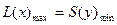 .
.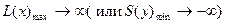 , то другая задача не имеет допустимых решений.
, то другая задача не имеет допустимых решений.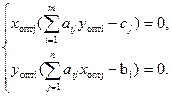
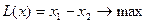 при ограничениях
при ограничениях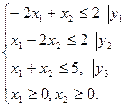
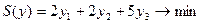 при ограничениях
при ограничениях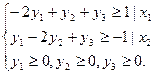

 , то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств
, то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств 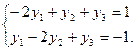 Подставим Х(опт) в систему ограничений исходной задачи.
Подставим Х(опт) в систему ограничений исходной задачи.
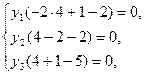
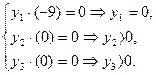
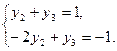 . ЕЕ решение Y(опт)=(0,2/3,1/3), при этом
. ЕЕ решение Y(опт)=(0,2/3,1/3), при этом 
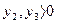 , то по второй теореме второе и третье неравенства обращаются в равенства, то есть
, то по второй теореме второе и третье неравенства обращаются в равенства, то есть 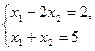 , решением которого является Х(опт)= (4,1).
, решением которого является Х(опт)= (4,1).


