
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 8. Линии второго порядка, их канонические уравнения, фокусы, директрисы., асимптоты.Содержание книги
Поиск на нашем сайте
Взаимное расположение прямых 4. Взаимное расположение прямых а) б) в) Угол между двумя прямыми определяется из формулы г) Расстояние между двумя скрещивающимися прямыми 5. Расстояние от точки М до прямой, заданной точкой М0 и направляющим вектором p:
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ Пусть прямая задана точкой а) Прямая и плоскость параллельны, если б) Прямая принадлежит плоскости, если в) Прямая и плоскость пересекаются, если В этом случае угол между прямой и плоскостью равен
Сложное отношение четырёх точек Пусть на проективной прямой заданы точки: А, В, С, D, так, что точки А, В и С различные, а точка D не совпадает с точкой А. Рассмотрим репер R0=(А, В, С) и обозначим координаты точки D (х1,х2)R, т.к. D не совпадает с т. А, то х2≠0. Число обозначаемое (АВ, СD)=х1/х2 называется сложным отношением четырёх точек. Теорема: Координатное представление сложного соотношения четырёх точек. Пусть в проективном репере т. А, В, С, D имеют координаты А(а1, а2), В(b1, b2), С(c1, c2), D(d1, d2), тогда Свойства сложного отношения четырёх точек. 1. (АВ, СD)=1/ (AB, DC), (АВ, СD)=1/(ВА, DС) 2. (АВ, CD)=(BA,DC) 3. (АВ, СD)=(СD, АВ) 4. (АВ, СС)=1, (АВ, СВ)=0 5. (АВ, СD) + (АС, ВD)=1 Доказательство проводится на основе определения сложного отношения при учете, что рассматривается репер (А, В, С), где А(1, 0), В(0, 1), С(1, 1). Зная сложное отношение четырёх точек А, В, С, D, можно найти сложное отношение всевозможных комбинаций этих точек. Говорят, что точки А, В гармонически разделяют точки С, D, если (АВ, СD)=-1. Алгоритм решения задач 1. Находим область допустимых решений системы ограничений задачи. 2. Строим вектор С. 3. Проводим линию уровня Lo, которая перпендикулярна С. 4. Линию уровня перемещаем по направлению вектора С для задач на максимум и в направлении, противоположном С, для задач на минимум. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума. Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум. Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми. 5. Находим координаты точки экстремума и значение целевой функции в ней. Пример: Выбор оптимального варианта выпуска изделий Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в табл.
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным? решение. Обозначим: x1 — суточный объем выпуска сливочного мороженого, кг; x2 — суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид L(x) = 16 x1 + 14 x2 -> max при ограничениях:
Решая систему, получим координаты точки D(312,5; 300), в которой и будет оптимальное решение, т.е. Х(опт)=(312,5;300), при этом Lmax(x)=16*312,5+14*300=9200р. Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р.
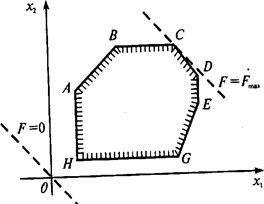
Идея симплексного метода (метода последовательного улучшения плана) заключается в том, что, начиная с некоторого исходного опорного решения, осуществляется последовательно направленное перемещение по опорным решениям задачи к оптимальному. Значение целевой функции при этом перемещении для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оптимальное опорное решение. Опорным решением называется базисное неотрицательное решение. Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому можно предложить такой способ решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограничений и выбрать среди них то, на котором функция цели принимает оптимальное решение. Геометрически это соответствует перебору всех угловых точек многогранника решений. Такой перебор, в конце концов, приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допустимых базисных решений хотя и конечно, но может быть чрезвычайно велико. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или, по крайней мере, "не хуже"), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума F-> max, уменьшение — при отыскании минимума F-> min). Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере. Пусть область допустимых решений изображается многоугольником ABCDEGH. Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем — к оптимальной точке С.
Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию. Рассмотрим две задачи I и II линейного программирования, обладающими следующими свойствами: 1. В одной задаче ищут максимум линейной функции, в другой — минимум. 2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой. 3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "<", а в задаче минимизации — все неравенства вида ">". 4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу. Различают симметричные, несимметричные и смешанные двойственные задачи. Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами. В дальнейшем для простоты будем называть их просто двойственными задачами. Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи. 1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду "≤", а если минимум — к виду "≥". Для этого неравенства, в которых данное требование не выполняется, умножить на -1. 2. Составить расширенную матрицу системы, в которую включить матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции. 3. Найти матрицу, транспонированную к данной матрице. 4. Сформулировать двойственную задачу на основании полученной матрицы и условия неотрицательности переменных. Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. ТЕОРЕМА 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений Х и Y выполняется равенство Если одна из двойственных задач неразрешима ввиду того, что ТЕОРЕМА 2. Для оптимальности допустимых решений Х и У пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой. Пример. Порешению исходной задачи найти решение двойственной, и наоборот. Исходная задача
Двойственная задача будет иметь вид:
Исходную задачу можно решить графически. Получим Х(опт)=(4,1), при этом L(x)=3. На основании первой теоремы двойственности Так как
Тогда система ограничений двойственной задачи примет вид С другой стороны, пусть дано решение двойственной задачи Y(опт)=(0,2/3,1/3), при этом По первой теореме Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле Y(опт)=С*А-1где С – матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи, А-1 –обратная матрица для матрицы А, являющейся матрицей коэффициентов базисных переменных системы ограничений исходной задачи в оптимальном решении. Двойственные задачи позволяют получить решение исходной задачи, если оно затруднительно или громоздко.
Вторая часть. Информатика. Примеры записи нечеткого множества Пусть E = {x1, x2, x3, x4, x5 }, M = [0,1]; A - нечеткое множество, для которого A(x1)=0,3; A(x2)=0; A(x3)=1; A(x4)=0,5; A(x5)=0,9. Тогда A можно представить в виде: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } или A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5, или
. Замечание. Здесь знак "+" не является обозначением операции сложения, а имеет смысл объединения. Пусть Х=(1,2.3.4,5,6,7,8,9.10). Тогда нечеткое множество «большие числа» может быть представлено следующим образом: А= «большие числа»=0,2/6+0,5/7+0,8/8+1/9+1/10. Это следует понимать следующим образом: 9 и 10 с абсолютной уверенностью можно отнести к «большим числам», 8 есть большое число со степенью 0,8, 1,2,3,4,5 абсолютно не являются большими числами. Функцию принадлежности можно изображать графически. Например, график функции принадлежности «Оптимальный возраст работника».
Видно, что возраст от 20 до 30 оценивается экспертами как бесспорно оптимальный, а от 60 и выше- как неоптимальный. В диапазоне от 35 до 60 эксперты проявляют неуверенность в своей классификации, структура которой передается графиком функции принадлежности. Примеры нечетких множеств Пусть E = {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько" можно определить следующим образом: "несколько" = 0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8; его характеристики: высота = 1, носитель={3,4,5,6,7,8}, точки перехода - {3,8}. Пусть E = {1,2,3,...,100} и соответствует понятию "возраст", тогда нечеткое множество "молодой", может быть определено с помощью "молодой"(x) = Нечеткое множество "молодой" на универсальном множестве E' ={Иванов, Петров, Сидоров,...} задается с помощью функции принадлежности "молодой"(x) на E = {1,2,3,..100} (возраст), называемой по отношению к E' функцией совместимости, при этом: "молодой"(Сидоров):= "молодой"(x), где x - возраст Сидорова. Например, известны следующие данные
Тогда данное множество можно описать следующим образом: ={1/18+0,96/26+0,02/64+0,34/32+0,003/85}
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями. В результате операций из исходных множеств получаются новые. Заде предложил набор аналогичных операций над нечеткими множествами через операцию с функциями принадлежности этих множеств. 1) Включение. Пусть A и B - нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если x E A(x) B(x). Обозначение: A B. Иногда используют термин "доминирование", т.е. в случае когда A B, говорят, что B доминирует A. 2) Равенство. A и B равны, если x E A(x) = B (x). Обозначение: A = B. 3) Дополнение. Пусть = [0,1], A и B - нечеткие множества, заданные на E. A и B дополняют друг друга, если xE A(x) = 1 - B(x). Обозначение: B = Очевидно, что 4) Пересечение. AB - наибольшее нечеткое подмножество, содержащееся одновременно в A и B. AB(x) = min(A(x), B(x)). 5) Объединение. А В - наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности: A B(x) = max(A(x), B(x)). 6) Разность. А - B = А A-B(x) = A 7) Дизъюнктивная сумма. АB = (А - B)(B - А) = (А A-B(x) = max{[min{ A(x), 1 - B(x)}];[min{1 - A(x), B(x)}] } Примеры. Пусть: A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4; B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4; C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4. Здесь: AB, т.е. A содержится в B или B доминирует A, С несравнимо ни с A, ни с B, т.е. пары {A, С} и {A, С} - пары недоминируемых нечетких множеств. A B C.
AB = 0,4/x1 + 0,2/x2 + 0/x3 + 1/x4. АВ = 0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4. А - В = А В - А = А В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4. Нечеткие отношения Пусть X={x1, x2, …..xn} Y={y1, y2, …,yм}. Нечетким отношением R называется нечткое множество, определенное на декартовом произведении X*Y, которому соответствует функция принадлежности Пример Пусть Х={конь, осел}, Y={мул, корова}. Нечеткое отношение»подобный» может быть определено следующим образом: R= «подобный»=0,8/(конь, мул)+0,4/(конь, корова)+0,9/(осел, мул)+0,5/(осел, корова), то есть конь похож на мула со степенью 0.8, конь похож на корову со степень. 0,4 и т.д. В любом случае степень истинности оказывается не числом из отрезка [0,1], а нечетким числом.
Содержание
1. Источники и виды погрешностей результата вычислительной задачи 2. Абсолютные и относительные погрешности Примеры решения задач Задача 1. Даны координаты вершин Найти: 1) длину стороны 2) уравнения прямых 3) угол 4) уравнение прямой, содержащей высоты 5) уравнение прямой, содержащей медианы 6) уравнение прямой, проходящей через точку 7) координаты точки Решение: 1. Расстояние между точками
2. Уравнение прямой, проходящей через две точки
Получили уравнения прямых линий с угловым коэффициентом, из которых имеем: 3. Тангенс угла Угол
4. Высота прямой
Уравнение прямой, проходящей через точку
Значит, уравнение прямой
Для того, чтобы найти длину высоты
В результате вычислений получены координаты точки 5. Чтобы найти уравнение прямой, содержащей медианы
Тогда уравнение прямой
И, наконец, координаты точки
6. Если две прямые параллельны, то можно сказать, что их уравнения отличаются только свободным членом. Значит, уравнение прямой, параллельной стороне
Известно, что
И тогда уравнение прямой будет иметь вид:
7. По условию точка
Значит,
Задача 2.
Даны вершины пирамиды: 1. длину стороны 2. площадь грани 3. угол 4. уравнение прямой 5. уравнение плоскости грани 6. уравнение высоты, опущенной из точки 7. точку, симметричную точке 8. объем пирамиды. Решение: 1. Длина стороны
2. Для нахождения площади грани
В нашей задаче
3. Угол 4. В пространстве уравнение прямой, проходящей через две точки
Тогда уравнения прямой
5. Плоскость грани
Подставляя координаты точек и вычисляя определитель, получим уравнение грани
6. Каноническое уравнение прямой в пространстве, заданной точкой По условию, прямая (высота), проходит через точку
Чтобы найти длину высоты, можно воспользоваться формулой для нахождения расстояния от точки В нашей задаче точка имеет координаты
7. Найдем координаты точки
Подставив
Пусть
8. Объем пирамиды следует рассчитать по формуле, выражающей геометрический смысл смешанного произведения векторов:
Задача 3. Даны координаты точек: | |||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 и
и  , заданных точками
, заданных точками 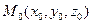 ,
,  и направляющими векторами
и направляющими векторами  соответственно определяется по следующим условиям:
соответственно определяется по следующим условиям: , но
, но 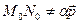 или
или 
 и
и 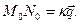
 ,
, 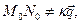 или смешанное произведение из трех определяющих векторов равно нулю:
или смешанное произведение из трех определяющих векторов равно нулю: 
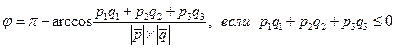
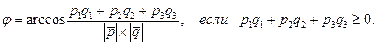


 , а плоскость – уравнением общего вида Ах + Ву + Сz +D = 0. Возможны следующие случаи их взаимного расположения:
, а плоскость – уравнением общего вида Ах + Ву + Сz +D = 0. Возможны следующие случаи их взаимного расположения: , а
, а 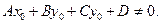


 .
.
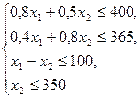
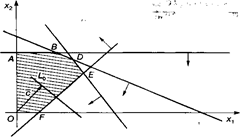 OABDEF — область допустимых решений. Строим вектор с(1,1). Линия уровня задается уравнением 16x1+14x2=const. Перемещаем линию уровня по направлению вектора с. Точкой выхода из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями:
OABDEF — область допустимых решений. Строим вектор с(1,1). Линия уровня задается уравнением 16x1+14x2=const. Перемещаем линию уровня по направлению вектора с. Точкой выхода из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями: 
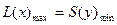 .
.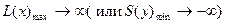 , то другая задача не имеет допустимых решений.
, то другая задача не имеет допустимых решений.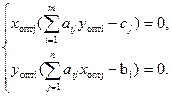
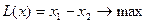 при ограничениях
при ограничениях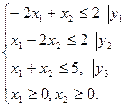
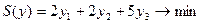 при ограничениях
при ограничениях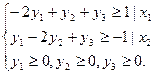

 , то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств
, то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств 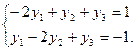 Подставим Х(опт) в систему ограничений исходной задачи.
Подставим Х(опт) в систему ограничений исходной задачи.
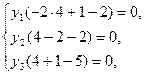
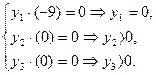
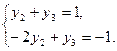 . ЕЕ решение Y(опт)=(0,2/3,1/3), при этом
. ЕЕ решение Y(опт)=(0,2/3,1/3), при этом 
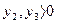 , то по второй теореме второе и третье неравенства обращаются в равенства, то есть
, то по второй теореме второе и третье неравенства обращаются в равенства, то есть 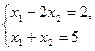 , решением которого является Х(опт)= (4,1).
, решением которого является Х(опт)= (4,1).
 .
. или A =
или A =  .
. = A. (Дополнение определено для M = [0,1], но очевидно, что его можно определить для любого упорядоченного M).
= A. (Дополнение определено для M = [0,1], но очевидно, что его можно определить для любого упорядоченного M). .
.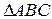 .
.  ,
,  ,
,  .
. ;
; и их угловые коэффициенты;
и их угловые коэффициенты; ;
;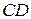 и ее длину;
и ее длину;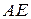 и координаты точки
и координаты точки  пересечения этой медианы с высотой
пересечения этой медианы с высотой  , расположенной симметрично точке
, расположенной симметрично точке  относительно прямой
относительно прямой  и
и 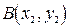 определяется по формуле:
определяется по формуле:  . Значит, длина стороны
. Значит, длина стороны  .
. . Подставляя в равенство координаты данных точек, получим уравнения прямых
. Подставляя в равенство координаты данных точек, получим уравнения прямых 



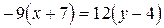







 ;
;  .
. между двумя прямыми, угловые коэффициенты которых соответственно равны
между двумя прямыми, угловые коэффициенты которых соответственно равны  и
и 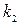 , вычисляется по формуле:
, вычисляется по формуле:  .
. ;
; 
 для прямой
для прямой 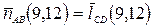
 :
:




 – точки пересечения прямых
– точки пересечения прямых 


 .
. как середину стороны
как середину стороны 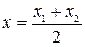 ;
; 






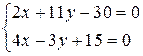
 ;
;  .
.
 эта прямая проходит через точку
эта прямая проходит через точку  , значит, координаты точки должны удовлетворять уравнению искомой прямой:
, значит, координаты точки должны удовлетворять уравнению искомой прямой:
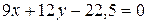 или после деления на 3:
или после деления на 3:
 . Воспользуемся уже известными формулами для определения координат середины отрезка:
. Воспользуемся уже известными формулами для определения координат середины отрезка: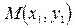 .
. и
и 


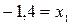
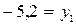
 .
. и
и 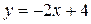 .
. ,
,  ,
,  ,
,  . Необходимо найти:
. Необходимо найти: ;
; ;
; ;
;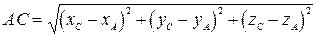
 .
.



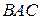 равен
равен 
 и
и  , имеет следующий вид:
, имеет следующий вид: , где t – некоторый параметр.
, где t – некоторый параметр.
 ,
,  ,
,  .
. и имеющую уравнение
и имеющую уравнение


 и направляющим вектором
и направляющим вектором  имеет вид:
имеет вид: 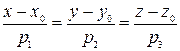


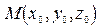 до плоскости
до плоскости  :
: 
 , а уравнение плоскости:
, а уравнение плоскости: 
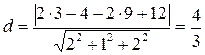 .
. ,
,  ,
,  через параметр в уравнение плоскости
через параметр в уравнение плоскости  :
: ,
,  ,
, 

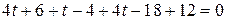 .
.



 ;
; 
 – точка, симметричная точке
– точка, симметричная точке  . Подставляя координаты точек в известные формулы для определения координат середины отрезка, получим координаты точки
. Подставляя координаты точек в известные формулы для определения координат середины отрезка, получим координаты точки  ,
,  ,
, 
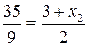 ,
, 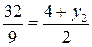 ,
, 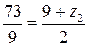
 ,
,  ,
, 
 .
.



