
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила записи приближенных чисел
Для решения инженерных задач часто приходится определять различные числа, как точные, так и приближенные. При этом требуется, чтобы погрешность, возникающая при округлении была бы минимальной. Пусть некоторое десятичное число представлено его разложением
где 10S – единица разряда S, aS – цифра разряда, S – номер разряда. Все цифры числа от первой слева, неравной нулю, до последней цифры справа называются значащими цифрами. Например, пусть заданы следующие числа:
a1 = 2.67; a2 = 0.267; a3 = 0.00267; a4 = 0.26700
Тогда для a1, a2, a3 имеем 3 значащие цифры и для a4 - 5 значащих цифр. Если крайние справа нули не считают значащими, то число записывают в экспоненциальной форме:
где m - экспонента, p – порядок числа. Значащая цифра числа aS называется верной, если абсолютная погрешность этого числа не превосходит половины единицы разряда S, т. е.
Если абсолютная погрешность числа не указана, то все его значащие цифры считают верными. Под округлением числа а будем понимать его замену числом а’, которое имеет меньшее количество значащих цифр, чем исходное число а. Округление должно производиться таким образом, чтобы возникающая ошибка была минимальной. Для оценки величины ошибки вводят следующие характеристики: - абсолютная погрешность округления - относительная погрешность округления При необходимости могут использоваться их предельные значения:
Если округляется приближенное число, то погрешность полученного числа включает две составляющие: - погрешность округления; - погрешность исходного числа. Округление чисел производится по следующим правилам. 5. Если первая из отбрасываемых цифр меньше 5, то последняя сохраняемая цифра не изменяется. 6. Если первая из отбрасываемых цифр больше 5, то последняя сохраняемая цифра увеличивается на 1. 7. Если первая из отбрасываемых цифр равна 5, и за ней идут не нули, то последняя сохраняемая цифра увеличивается на 1. 8. Если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней равны нулю, то последняя сохраняемая цифра увеличивается на 1, если она нечетная, и не изменяется, если она четная.
4. Погрешность суммы и разности приближенных чисел
Абсолютная погрешность алгебраической суммы или разности нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел:
Предельная абсолютная погрешность суммы или разности определяется следующим образом:
Оценим относительную погрешность
где Предельная относительная погрешность суммы двух чисел вычисляется как
где Формулы (1) и (2) можно обобщить на случай произвольного количества слагаемых:
Таким образом, при суммировании чисел одного знака не происходит потери относительной точности, что видно из приведенных соотношений. Оценка относительной погрешности для разности двух чисел осуществляется по формуле
Где
Формулы для предельных относительных погрешностей имеют вид:
Очевидно, что для разности приближенных чисел относительные погрешности возрастают в n раз, где n > 1. При этом возможна существенная потеря точности, которая происходит в том случае, если числа X1, X2 настолько близки, что их сумма значительно превышает их разность
5. Погрешности произведения и частного приближенных чисел
Формулы для оценки абсолютной погрешности произведения и частного является более сложными, чем для суммы и разности. Поэтому для частного и произведения абсолютные погрешности обычно определяют, используя известную формулу
для a = x1x2...xn или a = x1/x2, где относительная погрешность произведения приближенных чисел определяется следующим образом:
Формула показывает, что относительные погрешности нескольких приближенных чисел складываются при выполнении операции умножения над этими числами. Для предельной относительной погрешности формула имеет вид:
Аналогичным образом можно получить оценки погрешности частного двух приближенных чисел:
6. Погрешность функции
Основная задача теории погрешностей заключается в следующем: по известным значениям погрешностей исходных данных определить погрешность некоторой функции от этих величин. Пусть задана функция f(x), значение которой требуется вычислить для приближенного значения аргумента погрешность вычислительный приближенный функция
Считается, что формула справедлива, если относительные ошибки аргумента и результата малы по сравнению с единицей, т.е. dx0 << 1 и df(x0) << 1.
Нетрудно заметить, что вычисление функции в точке с большим модулем производной может привести к значительному увеличению погрешности результата по сравнению с погрешностью аргумента (катастрофическая потеря точности).
7. Погрешность функции нескольких переменных
Пусть y = f(x1, x2, …, xn) – приближенное значение функции от приближенных аргументов Для определения
где производная определяется по x1. Затем вычисляется частная ошибка, вносимая аргументом
В итоге искомая погрешность функции
Условиями применимости этой формулы считается выполнение следующих неравенств:
dxi << 1 (i =
8. Обратная задача теории погрешностей
Обратная задача теории погрешностей заключается в определении погрешностей исходных данных по заданной погрешности результата. С использованием понятия функции нескольких переменных эта задача формулируются следующим образом: определить предельные погрешности аргументов функции, чтобы погрешность функции в целом не превышала бы заданной величины. Эта задача является математически неопределенной, так как одна и та же погрешность результата может быть получена при разных погрешностях исходных данных. В простейшем случае для решения этой задачи используют принцип равных влияний, согласно которому в формуле для определения предельной абсолютной погрешности функции нескольких аргументов вида
все слагаемые из правой части принимаются равными:
Отсюда значения предельных абсолютных погрешностей аргументов определяются следующим образом:
Список литературы
1. Адаптивные телеизмерительные системы, под ред. А. Б. Фремке, М. 1981 г. 2. Левин, Плоткин, Цифровые системы передачи информации, 1982 г. 3. Свиридов Н. Г. Проектирование РТС передачи информации Рязань, РРТИ, 1988 г. Размещено на Allbest.ru Примеры решения задач Задача 1. Даны координаты вершин Найти: 1) длину стороны 2) уравнения прямых 3) угол 4) уравнение прямой, содержащей высоты 5) уравнение прямой, содержащей медианы
6) уравнение прямой, проходящей через точку 7) координаты точки Решение: 1. Расстояние между точками
2. Уравнение прямой, проходящей через две точки
Получили уравнения прямых линий с угловым коэффициентом, из которых имеем: 3. Тангенс угла Угол
4. Высота прямой
Уравнение прямой, проходящей через точку
Значит, уравнение прямой
Для того, чтобы найти длину высоты
В результате вычислений получены координаты точки 5. Чтобы найти уравнение прямой, содержащей медианы
Тогда уравнение прямой
И, наконец, координаты точки
6. Если две прямые параллельны, то можно сказать, что их уравнения отличаются только свободным членом. Значит, уравнение прямой, параллельной стороне
Известно, что
И тогда уравнение прямой будет иметь вид:
7. По условию точка
Значит,
Задача 2.
Даны вершины пирамиды: 1. длину стороны 2. площадь грани 3. угол 4. уравнение прямой 5. уравнение плоскости грани 6. уравнение высоты, опущенной из точки 7. точку, симметричную точке 8. объем пирамиды. Решение: 1. Длина стороны
2. Для нахождения площади грани
В нашей задаче
3. Угол 4. В пространстве уравнение прямой, проходящей через две точки
Тогда уравнения прямой
5. Плоскость грани
Подставляя координаты точек и вычисляя определитель, получим уравнение грани
6. Каноническое уравнение прямой в пространстве, заданной точкой По условию, прямая (высота), проходит через точку
Чтобы найти длину высоты, можно воспользоваться формулой для нахождения расстояния от точки В нашей задаче точка имеет координаты
7. Найдем координаты точки
Подставив
Пусть
8. Объем пирамиды следует рассчитать по формуле, выражающей геометрический смысл смешанного произведения векторов:
Задача 3. Даны координаты точек: 1) составить уравнение гиперболы, проходящей через эти точки, если ее фокусы расположены на оси 2) найти полуоси, эксцентриситет, фокусы; 3) написать уравнение гиперболы в полярной системе координат; 4) найти уравнения директрис и асимптот; 5) написать уравнения касательных к гиперболе в точке Решение: 1. Каноническое уравнение гиперболы имеет вид
Решая систему, например, способом сложения, получим:
2. Полуоси гиперболы – это числовые значения a и b: Эксцентриситет гиперболы – это число 3. В полярной системе координат уравнение гиперболы имеет вид:
Подставляем известные значения:
4. Директрисы гиперболы имеют уравнения Прямые, заданные уравнениями
5. Уравнение касательной к гиперболе, заданной уравнением Точка И тогда уравнение касательной будет следующим:
Вычисляем дискриминант квадратного уравнения:
Так как прямая и гипербола имеют одну общую точку, то это уравнение имеет единственное решение и
Значит, касательные задаются уравнением Задача 4. Определить вид заданной линии второго порядка, найти ее центр, векторы оси асимптотического направления, главные направления и главные диаметры.
Решение: Для определения вида заданной линии второго порядка упростим общее уравнение линии, чтобы свести к каноническому. Такое упрощение достигается при переходе к канонической системе координат посредством поворота осей системы на определенный угол и переноса начала в нужную точку. Поворот осей исходной системы В полученном после соответствующих преобразований уравнении необходимо выделить полные квадраты и реализовать перенос начала полученной системы координат. Таким образом, реализуется двойной переход: 1) от системы 2) от системы Единичные векторы главных направлений линии имеют координаты
Для их нахождения, а, следовательно, для упрощения уравнения заданной линии используем общую схему приведения уравнения линии II порядка к каноническому виду. Решаем характеристическое уравнение данной линии:
Его корни Находим угловые коэффициенты главных направлений:
Из курса тригонометрии известны формулы
Найдем координаты векторов
Очевидно, что наша линия второго порядка поворачивается на угол
В новой системе координат
Выделяя полные квадраты и преобразовывая, получаем уравнение эллипса в системе координат
Координаты нового начала координат
Вектор асимптотического направления должен иметь координаты
Для удобства выберем угловой коэффициент прямой асимптотического направления
Пусть
Главные диаметры описываются уравнениями:
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.21 с.) |
 ,
,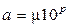 ,
, .
. ;
;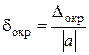 .
.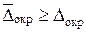 ;
; 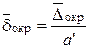 .
. ;
;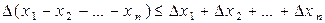 .
. ;
; .
. суммы приближенных чисел. Пусть Х1, Х2 - точные числа одного знака, х1, х2 - их приближения. Тогда
суммы приближенных чисел. Пусть Х1, Х2 - точные числа одного знака, х1, х2 - их приближения. Тогда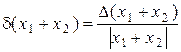 £
£ 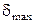 (1)
(1)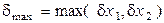 .
.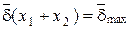 , (2)
, (2) .
.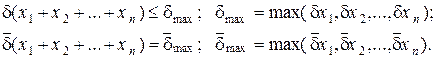
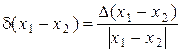 £ ndmax,
£ ndmax, .
.
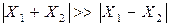 . Тогда n >> 1, что приводит к полной или почти полной потере точности. Такая ситуация называется катастрофической потерей точности.
. Тогда n >> 1, что приводит к полной или почти полной потере точности. Такая ситуация называется катастрофической потерей точности. ,
,

 ;
; 
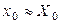 , имеющего известную предельную абсолютную погрешность
, имеющего известную предельную абсолютную погрешность  . Если функция f(x) дифференцируема в точке x0, то погрешность ее значения в этой точке можно оценить как
. Если функция f(x) дифференцируема в точке x0, то погрешность ее значения в этой точке можно оценить как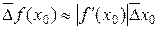 .
.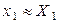 ,
, 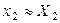 , …,
, …, 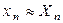 , которые имеют абсолютные ошибки
, которые имеют абсолютные ошибки 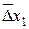 ,
, 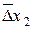 , …,
, …, 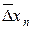 .
.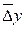 используют принцип наложения ошибок, согласно которому учитывают влияние погрешностей каждого из аргументов в отдельности, а затем полученные погрешности суммируют. Для этого вначале временно предполагают, что все аргументы, кроме x1 являются точными числами, и находится соответствующая частная ошибка, вносимая только погрешностью этого аргумента
используют принцип наложения ошибок, согласно которому учитывают влияние погрешностей каждого из аргументов в отдельности, а затем полученные погрешности суммируют. Для этого вначале временно предполагают, что все аргументы, кроме x1 являются точными числами, и находится соответствующая частная ошибка, вносимая только погрешностью этого аргумента 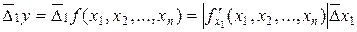 ,
,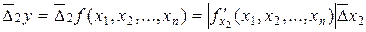 .
. .
. ); d f(x1, x2, …, xn) << 1.
); d f(x1, x2, …, xn) << 1.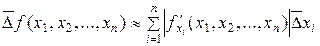 .
.
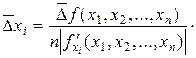
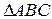 .
.  ,
,  ,
,  .
. ;
; и их угловые коэффициенты;
и их угловые коэффициенты; ;
;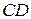 и ее длину;
и ее длину;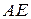 и координаты точки
и координаты точки  пересечения этой медианы с высотой
пересечения этой медианы с высотой  , расположенной симметрично точке
, расположенной симметрично точке  относительно прямой
относительно прямой  и
и 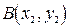 определяется по формуле:
определяется по формуле:  . Значит, длина стороны
. Значит, длина стороны  .
. . Подставляя в равенство координаты данных точек, получим уравнения прямых
. Подставляя в равенство координаты данных точек, получим уравнения прямых 



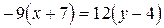







 ;
;  .
. между двумя прямыми, угловые коэффициенты которых соответственно равны
между двумя прямыми, угловые коэффициенты которых соответственно равны  и
и 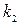 , вычисляется по формуле:
, вычисляется по формуле:  .
. ;
; 
 для прямой
для прямой 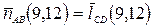
 :
:




 – точки пересечения прямых
– точки пересечения прямых 


 .
. как середину стороны
как середину стороны 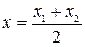 ;
; 






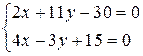
 ;
;  .
.
 эта прямая проходит через точку
эта прямая проходит через точку  , значит, координаты точки должны удовлетворять уравнению искомой прямой:
, значит, координаты точки должны удовлетворять уравнению искомой прямой:
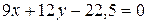 или после деления на 3:
или после деления на 3:
 . Воспользуемся уже известными формулами для определения координат середины отрезка:
. Воспользуемся уже известными формулами для определения координат середины отрезка: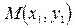 .
. и
и 


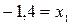
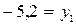
 .
. и
и 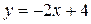 .
. ,
,  ,
,  ,
,  . Необходимо найти:
. Необходимо найти: ;
; ;
; ;
;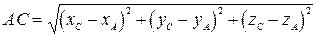
 .
.



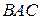 равен
равен 
 и
и  , имеет следующий вид:
, имеет следующий вид: , где t – некоторый параметр.
, где t – некоторый параметр.
 ,
,  ,
,  .
. и имеющую уравнение
и имеющую уравнение


 и направляющим вектором
и направляющим вектором  имеет вид:
имеет вид: 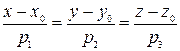


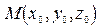 до плоскости
до плоскости  :
: 
 , а уравнение плоскости:
, а уравнение плоскости: 
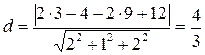 .
. ,
,  ,
,  через параметр в уравнение плоскости
через параметр в уравнение плоскости  :
: ,
,  ,
, 

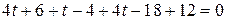 .
.



 ;
; 
 – точка, симметричная точке
– точка, симметричная точке  . Подставляя координаты точек в известные формулы для определения координат середины отрезка, получим координаты точки
. Подставляя координаты точек в известные формулы для определения координат середины отрезка, получим координаты точки  ,
,  ,
, 
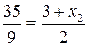 ,
, 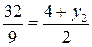 ,
, 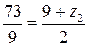
 ,
,  ,
, 
 .
.
 и
и 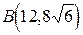 . Требуется:
. Требуется: ;
;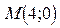 , в точке
, в точке 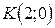 .
.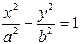 . По условию, точки
. По условию, точки  и
и 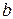 .
.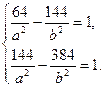
 и
и 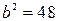 . И тогда искомое уравнение имеет вид:
. И тогда искомое уравнение имеет вид: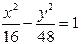 .
.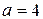 и
и 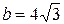 . Координаты фокусов гиперболы, расположенных на оси
. Координаты фокусов гиперболы, расположенных на оси 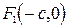 и
и 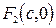 , где
, где 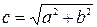 :
: 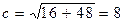 . Значит, координаты фокусов данной гиперболы:
. Значит, координаты фокусов данной гиперболы:  ,
, 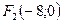 .
.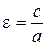 . Определяем его:
. Определяем его:  .
.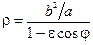 .
. .
. , в данном случае это будут прямые
, в данном случае это будут прямые 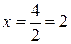 и
и  .
. и
и 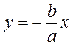 , называются асимптотами гиперболы; в данной задаче уравнения имеют вид:
, называются асимптотами гиперболы; в данной задаче уравнения имеют вид: 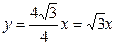 и
и 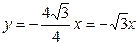 .
.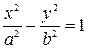 , в точке
, в точке 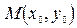 , лежащей на гиперболе, имеет вид:
, лежащей на гиперболе, имеет вид:  . Для
. Для 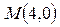 оно таково:
оно таково:  .
. не принадлежит гиперболе. Уравнение касательной можно записать в виде
не принадлежит гиперболе. Уравнение касательной можно записать в виде  (так как касательная – это прямая линия). Точка
(так как касательная – это прямая линия). Точка  ;
; 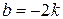 .
.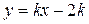 . Касательная и гипербола имеют единственную общую точку. Попробуем решить систему уравнений:
. Касательная и гипербола имеют единственную общую точку. Попробуем решить систему уравнений: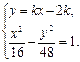
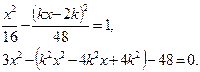
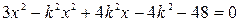 ,
,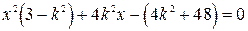 .
.
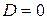 :
: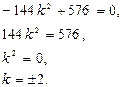
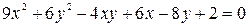 .
.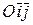 необходим лишь при присутствии в уравнении линии слагаемого, содержащего произведение
необходим лишь при присутствии в уравнении линии слагаемого, содержащего произведение 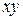 , и он реализуется на такой угол, чтобы уравнение линии в новой системе координат
, и он реализуется на такой угол, чтобы уравнение линии в новой системе координат  не содержало произведения. Такая система координат всегда присутствует, а направления осей этой системы называются главными направляющими линии II порядка.
не содержало произведения. Такая система координат всегда присутствует, а направления осей этой системы называются главными направляющими линии II порядка. .
.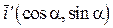 ,
, 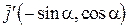 .
.
 .
. и
и  .
.
 .
.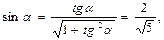
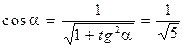 .
.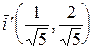 и
и  .
.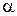 . Преобразования координат при повороте на угол
. Преобразования координат при повороте на угол 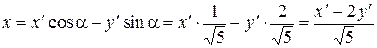 ,
, .
.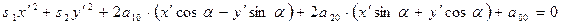 ,
, ,
,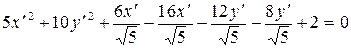 ,
,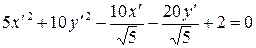 .
.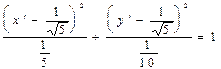 .
.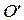 – центра линии II порядка – в системе
– центра линии II порядка – в системе 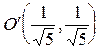 . Для нахождения координат центра линии в исходной системе координат
. Для нахождения координат центра линии в исходной системе координат 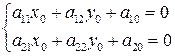
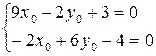 . Центр имеет координаты
. Центр имеет координаты  .
.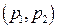 , удовлетворяющие условию:
, удовлетворяющие условию: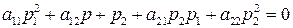 ,
, .
. , получим уравнение
, получим уравнение 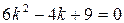 , которое не имеет корней, значит, у данной линии асимптотических направлений нет, что и должно быть: эллипс не имеет асимптотических направлений. Необходимым и достаточным условием главного направления
, которое не имеет корней, значит, у данной линии асимптотических направлений нет, что и должно быть: эллипс не имеет асимптотических направлений. Необходимым и достаточным условием главного направления 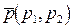 является условие
является условие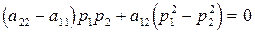 ,
,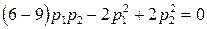 ,
,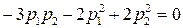 .
.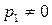 и
и 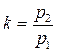 – угловой коэффициент главного направления,
– угловой коэффициент главного направления,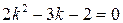
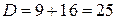
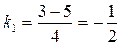 ,
, 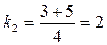 .
.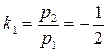 , значит, первый вектор главного направления имеет координаты
, значит, первый вектор главного направления имеет координаты 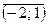 , аналогично
, аналогично 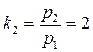 вторым вектором будет вектор
вторым вектором будет вектор 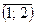 .
.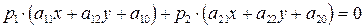 ,
,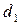 : –
: – 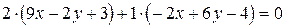 ,
,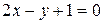 ,
,


