Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели, аппроксимации, и действительностьСодержание книги
Поиск на нашем сайте
Введение Вычисления в настоящее время может делать любой. Любой может также работать и скальпелем. Однако еще не решены все наши медицинские проблемы. - Карл Irikura Последние годы засвидетельствовали увеличение числа людей, использующих компьютерную химию. Многие из них - теоретики, и работают в химии большую часть времени над другими проблемами. Это увеличение было обеспечено развитием программного обеспечения, которое является все более и более легким в использовании. Теперь можно настолько легко использовать компьютерную химию, что вычисления могут быть выполнены без знания основных принципов. В результате, много людей вовлеченных в вычисления не понимают даже наиболее основных концепций. В результате их работа является в значительной степени непрофессиональной и зачастую третьесортной. Термин теоретическая химия может быть определен как математическое описание химии. Термин компьютерная химия – обычно используется, когда достаточно хорошо развит математический метод, и его можно автоматизировать для выполнения на компьютере. Обратите внимание, что термины " точные " и " совершенные " не появляются в этом определении. Очень немного аспектов в химии могут быть точно вычислены, но почти каждый аспект химии был описан в форме качественной или приблизительно количественной вычислительной схемы. Самая большая ошибка, которую может сделать химик при вычислениях, состоит в том, что он может полагать, что любое вычисленное значение является точным. Однако, также как совершенно не все линии спектра могут быть разрешены, часто качественное или приблизительное вычисление может давать полезное знание в химии, если исследователь понимает то, что он делает. Большинство химиков хочет избежать работы рукописного типа, которую теоретическая химия в ее наиболее истинной форме влечет за собой. Эта книга сосредоточится почти исключительно на знании, необходимом, чтобы эффективно использовать существующее программное обеспечение для молекулярного моделирования.
КАК ИСПОЛЬЗУЕТСЯ КОМПЬТЕРНАЯ ХИМИЯ Компьютерная химия используется различными путями. Один, особенно важный путь, состоит в том, чтобы смоделировать молекулярную систему до синтеза этой молекулы в лаборатории. Хотя вычислительные модели часто не совершенны, но они достаточно хороши, чтобы исключить 90 % возможных соединений неподходящих для их использования. Это - очень полезная информация, потому что синтез отдельного вещества может требовать месяцев работы и сырья, а также производить токсические выбросы. Второе использование компьютерной химии находится в более полном понимании проблемы. Есть некоторые свойства молекулы, которые могут быть получены в вычислительном отношении более легко, чем экспериментальными средствами. Есть также понимание в молекулярном связывании, которое может быть получено из результатов вычислений, которые не могут быть получены ни от какого экспериментального метода. Таким образом, много химиков экспериментаторов теперь используют вычислительное моделирование, чтобы получить дополнительное понимание о соединениях, исследуемых в своей лаборатории. Поскольку компьютерная химия стала более легкой, то профессиональные химики- компьютерщики изменили свое отношение к проблемам моделирования. Независимо от того, какой легкой бы компьютерная химия не становилась, будут всегда возникать проблемы настолько трудные, что только профессионал может заняться ими. ЧАСТЬ I Фундаментальные Принципы Эта глава, как предполагается, передает полное понимание теоретических принципов, на которых основаны вычислительные методы. Есть много доступных литературных источников, которые внесены в библиографический список. Эта книга предполагает, что читатель - химик и уже знаком с вводными курсами, использующими эти фундаментальные принципы. Эта глава даёт представление и терминологию, которая будет использоваться в остальной части книги. Здесь приводится напоминание нескольких ключевых теоретических пунктов, на которых основана вычислительная химия. ЭНЕРГИЯ Энергия - одна из наиболее полезных концепций в науке. Анализ энергии может предсказывать то, какие молекулярные процессы, вероятно, проходят или способны произойти. Все методы компьютерной химии определяют энергию такой, что система с самой низкой энергией является наиболее устойчивой. Таким образом, находят форму молекулы, которая соответствует самой низкой энергии. Вся энергия в системе часто делится на кинетическую энергию и потенциальную энергию. Кинетическая энергия может быть разделена на колебательное, поступательное и вращательное движение. Различие также сделано между кинетической энергией ядерного движения и электронного движения. Потенциальная энергия вполне может быть выражена через закон Кулона, и её можно разделить на энергию длин связей, изгибов связей, конформационной энергии, водородных связей и так далее. Химические процессы типа изменения длины связи или реакций, могут быть разделены на адиабатический (изоэнтропийный) и диабатические процессы. Адиабатные процессы - те, в которых система не изменяет состояние в ходе процесса. Диабатический, или неадиабатический, процессы - те, в которых изменение в электронном состоянии является частью процесса. Диабатические процессы обычно протекают с незначительным изменением энергии, изменяя состояние по мере необходимости. В математическом представлении молекул, необходимо определить систему отсчета, которая будет определена как нулевая энергия. Этот нуль энергии отличается от одной аппроксимации до другой. Для методов моделирования ab initio или теории Функционала плотности (DFT), все электроны в системе, имеют нулевую энергию, что соответствует расположению всех ядер и электронов на бесконечном расстоянии друг от друга. Полуэмпирические методы используют валентную энергию, которая соответствует наличию удаленных валентных электронов и получающихся из них ионов на бесконечном расстоянии. Несколько методов молекулярной механики используют как нулевую энергию стандартные химические состояния, и большинство используемых недеформированных молекул берется с нулевой энергией. Для некоторых методов молекулярной механики нулевая энергия может быть полностью произвольна. Даже в пределах определенной аппроксимации, полное значение энергии относительно нуля часто берется очень неточно. Совершенно понятно, что эта погрешность – будет почти всегда результатом систематической ошибки. Так, даже наиболее точные значения - это относительные энергии, полученные, вычитанием отдельных вычислений из полных энергий. Чрезвычайно точно может быть вычислено различие в энергии между конформерами и энергиями диссоциации связи ЭЛЕКТРОСТАТИКА Электростатика изучает из взаимодействий между заряженными объектами. Одна электростатика не может полностью описать молекулярные системы, но она очень важна для понимания взаимодействий электронов, которые описываются волновой функцией или электронной плотностью. Центральный столп электростатики - Закон Кулона, который является математическим описанием того, как одноименные заряды отталкиваются, и разноименные заряды притягиваются. Уравнения Закона Кулона для энергии и силы взаимодействия между двумя частицами с зарядами q1 и q2 на расстоянии r12 записываются так:
Обратите внимание, что эти уравнения не содержат константы, которые обычно включены во многие учебники, типа константы диэлектрической проницаемости в вакууме. Была разработана своя система единиц, которую назвали атомными единицами. В пределах этой системы единицы, многие из фундаментальных констант определены как имеющие значения = 1. В этой книге будут использоваться повсюду атомные единицы, если не будет сказано дополнительно. Другая очень полезная функция из электростатики это электростатический потенциал - Φ. Электростатический потенциал – функция, которая может быть определена в каждой точке реального трехмерного пространства. Если заряженная частица может быть добавлена к системе, без нарушения системы, то энергия распределяется в любой точке в пространстве – разделяясь на электростатические потенциальные заряды на этой частице. Часто используется такое требование, что не происходит никакого движения существующего заряда (поляризация электронной плотности) и что электростатический потенциал является энергией размещения бесконечно малого точечного заряда в системе. Применение электростатических потенциалов к химическим системам будет обсуждено далее в Главе 13. Формулировка Закона Кулона выше предполагает, что заряды отделены вакуумом. Уравнение Пуассона связывает электростатический потенциал Φ с плотностью заряда ρ Уравнение Пуассона. АТОМНЫЕ ЕДИНИЦЫ Система атомных единиц была развита, чтобы упростить математические уравнения, приравнивая многие фундаментальные константы к 1. Это - средства для теоретиков, которые проводят расчеты с помощью карандаша, и могут исключить, таким образом, возможные ошибки. Это также уменьшает и количество компьютерного времени, необходимого чтобы провести химические вычисления, которые могут быть очень длительны. Третье преимущество - любые изменения в измеренных значениях физических констант не затрагивают теоретические результаты. Некоторые теоретики работают полностью в атомных единицах, но много исследователей преобразовывают их теоретические результаты в более знакомые системы единицы. Таблица 2.1 дает некоторые коэффициенты пропорциональности для атомных единиц. ТЕРМОДИНАМИКА Термодинамика - одно из наиболее хорошо-развитых математических описаний химии. Термодинамика определяет многие из концепций энергии, свободной энергии и энтропии. См текст в книгах по физической химии. Очень часто, любая термодинамическая обработка может быть точно описана очень простыми математическими выражениями. Результаты вычислений могут быть связаны с термодинамикой. Результатами вычислений могут быть - внутренние энергии, свободные энергии и так далее, в зависимости от сделанного вычисления. Аналогично, возможно, вычислять различные значения энтропии. Однако, вычислительное программное обеспечение не всегда делает очевидным то, какая энергия вносится в это значение, что происходит из-за различий в терминологии между компьютерной химией и термодинамикой. Некоторые из этих различий будут отмечены в соответствующем месте этой книги. КВАНТОВАЯ МЕХАНИКА Квантовая механика (QM) - правильное математическое описание поведения электронов в молекуле и таким образом в химии. Теоретически QM может точно предсказывать любое свойство индивидуального атома или молекулы. Практически, уравнения QM, были точно решены только для одноэлектронных систем. Бесчисленное количество методов было развито, чтобы аппроксимировать решение для многоэлектронных систем. Эти аппроксимации могут быть очень полезны, но это вызывает сложность для исследователя, так как он должен знать, когда какая аппроксимация имеет силу и насколько точный будет результат. Значительная часть этой книги дает ответы на эти вопросы. Две эквивалентных формулировки QM были даны Шрёдингером и Гейзенбергом. Здесь, мы представим только формулировку Шрёдингера, так как она лежит в основе почти всех мето дов компьютерной химии. Уравнение Шрёдингера Где Н - оператор Гамильтониана, ψ - волновая функция и E - энергия. На языке математики, уравнение в этой форме называется собственным уравнением. ψ -тогда называется собственной функцией и E - собственное значение. Оператор и собственная функция могут быть соответственно матрицей и вектором, но это - не во всех случаях. Волновая функция ψ - функция электрона и положения ядер. Название подразумевает, что она описывает электрон как волну. Она - вероятностное описание поведения электрона. Также, она может описывать вероятность нахождения электронов в некоторых местоположениях, но не может предсказывать точно, где электроны расположены. Волновая функция также называется амплитудой вероятности, потому что - квадрат волновой функция это значение вероятности. Это единственно строго правильное значение волновой функции. Чтобы получить физически уместное решение уравнения Шрёдингера, волновая функция должна быть непрерывна,однозначна, нормирована, и антисимметрична относительно обмена электронами. Оператор Гамильтониана ^ Н, вообще определяется через уравнения, где
Где Но в настоящее время в доступном программном обеспечении, такой Гамильтониан почти никогда не используется. Проблема может быть упрощена, отделяя ядерные и электронные движения. Это называется аппроксимацией Борна-Опенгеймера. Гамильтониан для молекулы с постоянными ядрами: Здесь, первый член - только кинетическая энергия электронов. Второй - взаимодействия электронов с ядрами. Третий - отталкивание между электронами. Отталкивание между ядрами может быть добавлено к этой энергии в конце вычисления. Движение ядер может быть описано, рассматривая эту полную формулу, на поверхности потенциальной энергии, по которой двигаются ядра. Как только волновая функция будет определена, любое свойство индивидуальной молекулы может быть определено. Это можно сделать, беря значение используемого оператора для этого свойства, что обозначено угловыми скобками <>. Например, энергия ожидаемое значение, данного оператора Гамильтониана, Для точного решения, подобно энергия определяется уравнением Шрёдингера. Для приблизительной волновой функции, вводят аппроксимацию энергии и она является основанием для многих методов, описанных в последующих главах. Это называется вариационной энергией, потому что значение всегда больше чем точная энергия. Используя различные операторы. Можно получить различные наблюдаемые свойства, типа дипольного момента или электронной плотности. Другие свойства, кроме энергии - не вариационны, так как используется только Гамильтониан, чтобы получить волновую функцию в широко используемых методах компьютерной химии. Другой путь получения молекулярных свойств состоит в том, чтобы использовать теорему Hellmann-Feynman. Из этой теоремы, производная энергии относительно некоторого свойства P дается выражением: Это соотношение часто используется для вычисления электростатических свойств. Не все методы последовательных приближений подчиняются теореме Hellmann-Feynman. Только вариационные методы используют теорему Hellmann-Feynman. Некоторые из вариационных методов, которые будут обсуждены в этой книге - обозначены ХФ, MCSCF, CI, и CC. СТАТИСТИЧЕСКАЯ МЕХАНИКА Статистическая математическая механика, может вычислять термодинамические свойства веществ в массе из большого числа молекул и используется для описания материалов. Многое из статистической механики - все еще находится в рукописной стадии теории и не переложено в компьютерные программы. Так как квантовая механика не может точно решить уравнение Шрёдингера, то статистическая механика действительно не имеют даже исходной точки для строгой точной обработки. Несмотря на это ограничение, некоторые очень полезные результаты для веществ в большой массе могут быть получены. Вычисления статистической механикой часто проводят в конце ab initio вычислений колебательных частот для свойств в газовой фазе при низком давлении. Для изучения свойств конденсированных фаз, чтобы получить статистические данные, часто необходимы молекулярная динамика или вычисления Монте-Карло. Далее следуют принципы, на которых это возможно сделать. Рассмотрим некоторое количество жидкости, скажем, каплю воды, которая составлена из N индивидуальных молекул. Чтобы описать геометрию этой системы, если мы принимаем молекулы как твердые несжимаемые частицы, а каждая молекула должна быть описана шестью числами: три, чтобы указать её положение и три, чтобы описать его вращательную ориентацию. Это 6N размерное пространство называется фазовым пространством. Динамические вычисления должны дополнительно включать еще набор скоростей. Индивидуальная точка в фазовом пространстве, обозначенном Г, соответствует специфической геометрии всех молекул в системе. Есть много точек в этом фазовом пространстве, которые, никогда не будут встречаться ни в какой реальной системе, типа конфигураций с двумя атомами в одном и том же месте. Чтобы описывать реальную систему, необходимо определить то, какие конфигурации могут встречаться и указать вероятность их местонахождения. Вероятность появления конфигурации – это функция энергии данной конфигурации. Эта энергия - сумма потенциальной энергии из межмолекулярных сил притяжения или отталкивания и кинетической энергии из-за молекулярного движения. Для идеального газа, только кинетическая энергия должна рассматриваться. Для молекулярного газа, кинетическая энергия составлена из поступательного, вращательного, и колебательного движения. Для идеального одноатомного газа, энергия зависит только от поступательного движения. Для простоты обсуждения, мы обратимся к энергии системы или молекулы без дифференцирования типа энергии. Есть различие между энергией системы, составленной из всех молекул, и энергии индивидуальных молекул. Количество энергии в полной системе измеряется как температура системы. Однако, не все молекулы будут иметь одну и ту же энергию. Индивидуальные молекулы будут иметь большую или меньшую энергию, в зависимости от их движения и взаимодействия с другими молекулами. Есть некоторое вероятное распределения молекул с любой данной энергией. Это вероятность зависит от температуры T системы. Функция, которая дает отношение числа молекул, Ni, с различными энергиями, Ei, к числу молекул в состоянии j - распределение Больцмана, которое выражено уравнением: Где kb - константа Больцмана, 1,38066 *10-23 J/K. Уравнение (2.10) имеет силу, тогда когда есть равное число путей поместить систему в оба состояния энергии. Очень часто, есть большее количество состояний, доступных с высшими энергиями из-за увеличения числа вырожденных состояний. Когда это встречается, процент молекул в каждом состоянии определяется, умножая ранее записанное уравнение на число доступных состояний. Таким образом, часто имеется большая вероятность обнаружения высокоэнергетических молекул при высоких температурах как показано на рисунке 2.1. Обратите внимание, что основное состояние может быть недостаточной аппроксимацией к среднему числу. Когда некоторое свойство системы измерено экспериментально, то результат – это среднее число для всех молекул с соответствующими им энергиями. Это найденное количество - среднее статистическое число, называемое утяжеленным средним числом. Оно передает результат, полученному, определяя свойство для каждого возможного состояния энергии системы A(Г), и умножения вероятности обнаружения системы в том же состоянии энергии, w(Г). Это утяжеленное среднее число должно быть нормализовано функцией разделения Q, Это методика для обнаружения утяжеленного среднего числа используется для свойств идеального газа и квантово-механических систем с квантованными энергетическими уровнями. Это - не очень удобный способ проектировать компьютерные моделирования для реального газа или конденсировано фазовых систем, потому что определение каждого возможного состояния энергии ни в коем случае не тривиальная задача. Могут возникать также и систематические ошибки, которые не отражены этим соотношением. Другой путь решения этой проблемы состоит в том, чтобы использовать производные функции разделения без функции веса. Это можно сделать, используя следующие соотношения:
Другие термодинамические функции могут быть вычислены из этих значений. Это - не идеальный способ чтобы вычислять свойства из-за потребности определять состояние полной энергии системы, Q. Самое трудное получить точное значению для энтальпийного значения A, S и G, потому что они значительно зависят от высокоэнергетического состояния, которого система достигает нечасто. Эти функции зависят от фактического значения Q, а не только его производных. Есть несколько других, эквивалентных способов получить среднее статистическое значение. Один из них должен использовать среднее значение времени. В этой формуле, вычисление предназначено, для того чтобы моделировать движение молекул. При каждом шаге в моделировании, свойство будет вычислено для одной молекулы и усреднено одинаково на время всех шагов. Это будет эквивалентно утяжеленному среднему числу, потому что больший процент времени молекула будет находиться в наиболее вероятной энергии. Точность этого результата зависит от числа шагов времени и способности моделирования, чтобы правильно описать, как реальная система будет вести себя. Другая методика усреднения - использование понятия среднего значение ансамбля. Моделирование часто включают тысячи молекул. Значение может быть усреднено включением каждого результата для каждой молекулы в моделировании. Это соответствует концепции ансамбля молекул и таким образом называется средним значением ансамбля. Часто наиболее эффективно объединить средние числа времени и средние числа ансамблей, таким образом, составляющие в среднем все молекулы по многим шагам времени. Другой тип свойств для исследования - геометрическая ориентация молекул. Набор Декартовых координат опишет точку в фазовом пространстве, но это не передает статистическую тенденцию молекул, чтобы ориентировать их определенным способом. Это статистическое описание геометрии дается радиальной функцией распределения, также называемой функцией распределения пары. Эта - функция, которая дает вероятность обнаружения между атомами обособленно различными интервалами. Радиальная функция распределения дает индикацию относительно фазового поведения, как показано на рисунке 2.2. Большее количество подробностей может быть получено, используя определенные атомом радиальные функции распределения, типа вероятности обнаружения атомом водорода на различных расстояниях от атома кислорода. Сопоставление между моделированием и термодинамикой можно провести и дальше. Моделирования могут быть установлены так, чтобы использовать постоянный объем, давление, температуру и так далее. Некоторые из наиболее сложных моделирований - это многокомпонентные фазы или фазовые переходы. Эти методы обсуждены далее в Главе 7.
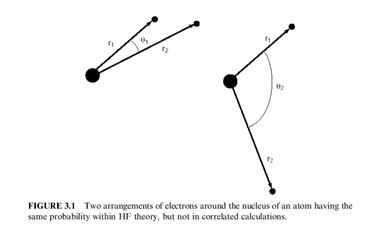
Методы Ab initio Термин ab initio - с латинского " с начала". Это название дается вычислениям, которые получены непосредственно из теоретических принципов без включения экспериментальных данных. Это - приблизительное квантовомеханическое вычисление. Используемые аппроксимации, - обычно математические аппроксимации, типа использования более простой функциональной формы для функции или обнаружения приблизительного решения дифференциального уравнения. АППРОКСИМАЦИЯ ХАРТРИ-ФОКА Наиболее общий тип ab initio вычисления называется вычислением Хартри-Фока (упрощенно HF), в котором первичная аппроксимация является аппроксимацией центрального поля. Это означает, что Кулоновское электрон-электронное отталкивание будет принято во внимание, объединяя все отталкивания. Это дает средний эффект отталкивания, но не явное взаимодействие отталкивания. Это - вариационное вычисление, означает, что приблизительные все расчетные энергии являются равными или большими чем точная энергия. Энергии рассчитаны в единицах по имени Хартри (1 Хартри = 27.2116 eV). Из-за аппроксимации центрального поля, энергии из вычислений HF всегда больше, чем точная энергия и при улучшении базисного набора имеют тенденцию идти к предельному значению называемому пределом Хартри-Фока,. Одно из преимуществ этого метода - он переводит многоэлектронное уравнение Шрёдингера в намного более простые одноэлектронные уравнения. Каждое одноэлектронное уравнение будет решено, чтобы выдать одноэлектронную волновую функцию, называемую орбиталью, и энергию, называемую орбитальной энергией. Орбиталь описывает поведение электрона в поле всех других электронов. Вторая аппроксимация в вычислениях HF возникает вследствие того, что волновая функция должна быть описана некоторой математической функцией, которая известна точно только для нескольких одноэлектронных систем. Функции, используемые наиболее часто – это линейные комбинации орбиталей гауссова типа exp (-ar2), аббревиатура GTO. Волновая функция будет сформирована из линейных комбинаций атомных орбиталей или более правильно, из линейных комбинаций базисных функций. Из-за этой аппроксимации, большинство вычислений HF дает вычисленную энергию большую, чем предел Хартри-Фока. Точный набор используемых базисных функций часто определяется сокращением, типа STO-3G или 6-311 ++ **. Базисные наборы обсуждены далее в Главах 10 и 28. Функции Gaussian должны быть умножены на угловую функцию, чтобы дать симметрию s, p, d орбиталей и так далее. Постоянные угловые моменты характерны для s симметрии. Угловые значения x, y, z дают симметрию для p. Угловые значения xy, xz, yz, x2-y2, 4z2-2x2-2y2 дают d симметрию. Это образец может быть продолжен и для других орбиталей. Эти орбитали будут объединены в детерминант. Это сделано для того, чтобы удовлетворить двум требованиям квантовой механики. Первое требование - электроны должны быть неразличимы. При линейной комбинации орбиталей на каждой орбитали имеется отдельный электрон, и можно говорить только, что электрон был помещен на новую орбиталь, но нельзя различить какой это электрон. Второе требование - волновая функция для фермионов (электрон это фермион) должна быть антисимметрична относительно обмена двумя частицами. Таким образом, если электрон 1 и электрон 2 переместить, должен измениться только знак полной волновой функции. Это определено детерминантом, потому что перемещение двух электронов эквивалентно обмену двумя колонками детерминанта, который изменяет его знак. Функции, помещенные в детерминант не должны быть индивидуальными функциями GTO, и называются примитивами Gaussian. Они могут быть утяжеленной суммой базисных функций на том же самом атоме или на различных атомах. Сумма функций на том же самом атоме часто используются, чтобы сделать быстрее вычисление, выполнение обсуждено в Главе 10. Суммы базисных функций на различных атомах используются, чтобы придать орбиталям специфическую симметрию. Например, молекула воды с C2v симметрией будет иметь орбитали, которые обозначаются как A1, A2, B1, B2, и являются неприводимыми представлениями точечных групп для C2v. Получающиеся орбитали, которые используют функции от нескольких атомов, называются молекулярными орбиталями. Это сделано для того, чтобы намного быстрее провести вычисление. Шаги в вычислении Хартри-Фока начинаются с начального приближения для орбитальных коэффициентов, обычно используя полуэмпирический метод. Эта функция используется, чтобы вычислить энергию и новый набор орбитальных коэффициентов, которые могут снова использоваться, чтобы получить новый набор и так далее. Эта процедура продолжается многократно, пока энергии и орбитальные коэффициенты не остаются постоянными при переходе от одного расчета до следующего. Это вычисление называется сходимостью. Нет никакой гарантии, что вычисление всегда будет сходиться. В случаях, когда это не происходит, требуется техническая экспертиза, чтобы решить проблему, и это обсуждено в Главе 22. Эта повторяющаяся процедура называется процедурой самосогласования поля (SCF). Некоторые исследователи обращаются к вычислению SCF, чтобы отличить их от более раннего метода, созданного Хартри, но процедура HF используются более широко. Можно провести изменение в процедуре HF – указав путь, по которому были созданы орбитали, чтобы отразить спаренные или неспаренные электроны. Если молекула имеет синглетный спин, то та же самая орбитальная пространственная функция может использоваться и для α и β электронов, для указания спина в каждой паре. Это называется ограниченным методом Хартри-Фока (RHF). Есть два метода HF для построения волновых функций молекул с неспаренными электронами. Одна методика может использовать два полностью отдельных набора орбиталей для α и β электронов. Это называется неограниченной волновой функцией Хартри-Фока (UHF) и означает, что спаренный электрон не будет иметь того же самого пространственного распределения. Это дает ошибку в вычислении, называемую загрязнением спина. В зависимости от типа расчетной химической системы загрязнение спина может представлять незначительную ошибку или ошибка может быть достаточно большая, чтобы сделать результаты непригодными. Загрязнение спина будет обсуждено более подробно в Главе 27. UHF вычисление популярно, потому что оно легко осуществляется и довольно эффективно выполняется. Другой путь построения волновой функции для молекул с открытой оболочкой – ограниченно открытый метод Хартри-Фока (ROHF). В этом методе, спаренный электроны совместно используют ту же самую пространственную орбиталь; таким образом, нет никакого загрязнения спина. Методику ROHF более трудно осуществить, чем UHF и может потребоваться большее количество времени CPU, для его выполнения. ROHF прежде всего используется для случаев, где имеет большое значение загрязнение спина. Для молекул с синглетным спином, RHF и UHF волновые функции почти всегда одинаковы. RHF волновые функции используются для синглетов, потому что их вычисление требует меньшего количества времени CPU. В некоторых редких случаях, синглетная молекула имеет резонансные структуры, типа бирадикала, и тогда даст лучшее описание молекулы UHF (например - озон). Схема RHF предполагает для электронов, что они остаются спаренными и означает, что вычисление будет не в состоянии отражать случаи, где пары электронов должны расщепиться. Например, ряд RHF вычислений для H2 с последовательным удлинением связи покажет, что H2 диссоциирует скорее на ионы Н+ и H-, чем на два атома Н. Это ограничение должно рассматриваться всякий раз, когда в процессе происходит моделирование образования и разрыва электронных пар. Эти расчеты ответственны и за некоторые систематические ошибки в результатах HF, типа энергий активации, которые могут быть завышены, а длины связи слегка слишком короткие, колебательные частоты слишком высокими, а дипольные моменты и заряды атома являются слишком большими. Волновые функции UHF обычно правильно учитывают диссоциацию. Есть множество других технических деталей, связанных с HF и другими ab initio методами, которые обсуждены в других главах. Базисные наборы и ошибка суперпозиции базисных наборов обсуждены более подробно в Главах 10 и 28. Для систем с открытой оболочкой, накладываются дополнительные условия: поляризация спина, изменение симметрии и загрязнение спина. Они обсуждены в Главе 27 КОРРЕЛЯЦИЯ Одно из ограничений вычислений HF - они не включают электронную корреляцию и означает, что HF принимает во внимание только среднее значение электронного отталкивания, но не явное взаимодействие электрон-электрон. В пределах теории HF вероятность обнаружения электрона на некотором местоположении в атоме определена расстоянием от ядра, а не расстоянием по отношению к другим электронам, как показано на рисунке 3.1. Это физически неверно, но это - следствие аппроксимации центрального поля, которую определяет метод HF. Множество типов вычислений начинают с вычисления HF и затем исправляют с помощью корреляции. Некоторые из этих методов - теория возмущения Мёллер-Плессета (MPn, где n - порядок исправления), метод обобщенной валентной связи (GVB), мультиконфигурационное самосогласованное поле (MCSCF), Конфигурационное взаимодействие (CI), и теория соединенных кластеров (CC). Эта группа методов будет упомянута как коррелированные вычисления. Корреляция важна по многим различным причинам. Включение корреляции обычно улучшает точность вычисленных энергий и молекулярных конфигураций. Для органических молекул, корреляция - дополнительное исправление для работы очень высокой точности, но она обычно не нужна, чтобы получить количественные результаты. Одно исключение, соединения, показ
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.011 с.) |

 (2.1)
(2.1) (2.2)
(2.2) Если заряд отделен некоторой средой континуума (сплошной среды), это взаимодействие будет изменено включением диэлектрической проницаемости для этой среды. Для описания молекул, правильно предположить, что ядра и электроны находятся в вакууме. Однако, диэлектрические эффекты часто включаются при описании эффектов растворителей, как описано в Главе 24.
Если заряд отделен некоторой средой континуума (сплошной среды), это взаимодействие будет изменено включением диэлектрической проницаемости для этой среды. Для описания молекул, правильно предположить, что ядра и электроны находятся в вакууме. Однако, диэлектрические эффекты часто включаются при описании эффектов растворителей, как описано в Главе 24. Оно может быть решено в цифровой форме или в пределах некоторой аналитической аппроксимации. Уравнение Пуассона используется, чтобы получить электростатические свойства молекул.
Оно может быть решено в цифровой форме или в пределах некоторой аналитической аппроксимации. Уравнение Пуассона используется, чтобы получить электростатические свойства молекул.
 (2.5)
(2.5)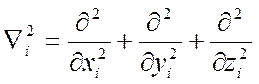 (2.6)
(2.6) - оператор Лапласиана, действующий на частицу i. Частицы являются электронами и ядрами. Символы mi и qi - масса и заряд частицы i, и rij - расстояние между частицами. Первое слагаемое дает кинетическую энергию частицы в пределах волновой формулировки. Второе слагаемое - энергия Кулоновского притяжения или отталкивания частиц. Эта формула – зависимое от времени нерелятивистическое уравнение Шрёдингера. Дополнительные условия могут появляться в Гамильтониане, когда принцип относительности или взаимодействия с электромагнитным излучением или полями могут быть приняты во внимание.
- оператор Лапласиана, действующий на частицу i. Частицы являются электронами и ядрами. Символы mi и qi - масса и заряд частицы i, и rij - расстояние между частицами. Первое слагаемое дает кинетическую энергию частицы в пределах волновой формулировки. Второе слагаемое - энергия Кулоновского притяжения или отталкивания частиц. Эта формула – зависимое от времени нерелятивистическое уравнение Шрёдингера. Дополнительные условия могут появляться в Гамильтониане, когда принцип относительности или взаимодействия с электромагнитным излучением или полями могут быть приняты во внимание. (2.7)
(2.7) (2.8)
(2.8)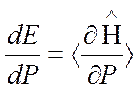 (2.9)
(2.9)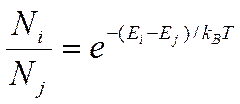
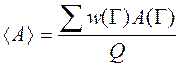 (2.11) где
(2.11) где  (2.12)
(2.12)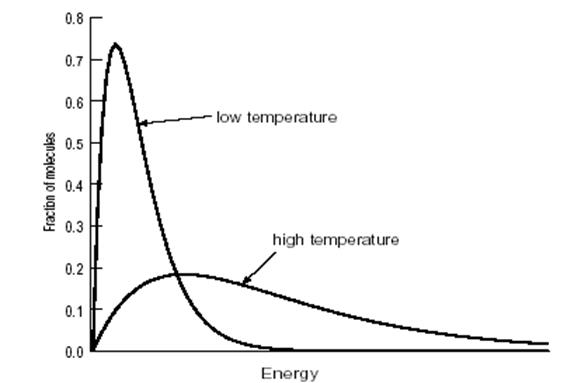 Однако, хороший результат может быть получен осуществлением выборкой состояний. Эти значения результатов, имеют статистическую неопределенность, которая связана с числом состоянии с отбираемым М.
Однако, хороший результат может быть получен осуществлением выборкой состояний. Эти значения результатов, имеют статистическую неопределенность, которая связана с числом состоянии с отбираемым М. 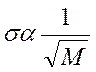 (2.13)
(2.13)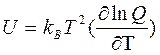 (2.14)
(2.14)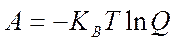 (2.15)
(2.15)
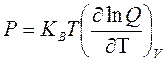 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19)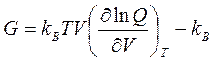 T ln Q (2.20)
T ln Q (2.20)