Моделирование последовательностной схемы

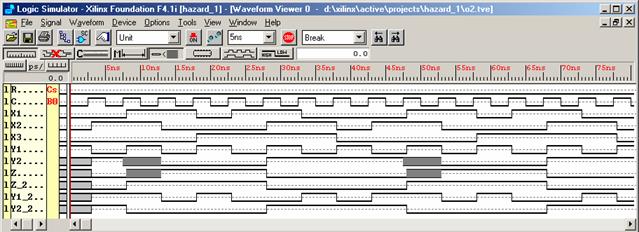
Следует отметить, что при проведении эксперимента ошибоч- ный переход может и отсутствовать. Все зависит от реального со- отношения задержек в цепях, определяющих порядок изменения сигналов обратной связи Y 1 и Y 2.

Для того чтобы убедиться, возможен предсказанный на ленте

ошибочный переход или нет, следует:

выполнить моделирование схемы с использованием единичных задержек элементов на полной последовательности смежных входных состояний;

затем реализовать временное моделирование схемы, предвари- тельно подсоединив макроэлементы лабораторного стенда и вы- полнив размещение проекта на кристалл;

сделать заключение о реальности ошибочного перехода схемы. На рис. 6.20 приведены результаты одновременного моделирова-

ния схем, изображенных на рис. 6.9 и 6.16, с единичными задержка- ми элементов. На рис. 6.20(а) временная диаграмма воспроизводит отрезок времени, приведенный в табл. 6.6, а на рис. 6.20(б) — де- тальный фрагмент указанной временной диаграммы.

Как видно, система моделирования неопределенное состояние элементов схемы в начальный момент времени (x 1 x 2 = 00) отобра- жает светло-серым цветом (см. рис. 6.20).

 

 

 

 

а)

б)

Рис. 6.20. Временные диаграммы работы схемы с единичными задержками элементов

 

Из сопоставления выходных сигналов z и z_2 одной и другой схем видно, что первая схема, содержащая условия для критиче- ских состязаний, ведет себя некорректно при переходе из состоя- ния x 1 x 2 = 01, y 1 y 2 = 01 в состояние x 1 x 2 = 11, y 1 y 2 = 10 (см. табл. 6.6). Более детальное рассмотрение этого перехода (см. рис. 6.20(б)) обнаруживает, что схема генерирует на входном набо- ре x 1 x 2 = 11. Это обстоятельство является следствием используемо- го метода моделирования и транспортной модели единичной за- держки элемента.

Схема, не содержащая условий для критических состязаний сигналов (см. рис. 6.16 и 6.20), функционирует правильно в соот- ветствии с заданным законом поведения.

На рис. 6.21 приведены временные диаграммы поведения ука- занных схем с учетом фактических задержек элементов и задержек в линиях связи, полученных в результате размещения элементов схем на кристалле. Здесь уже не наблюдается генерация первой схемы. Но из рассмотрения временных диаграмм видно, что оши- бочная работа первой схемы (см. рис. 6.9) из-за критических состя- заний сигналов происходит во всех предсказанных в ленте табл. 6.6 переходах. Вторая схема функционирует безошибочно.

Таким образом, остается только убедиться в правильности ука- занных предсказаний, выполнив загрузку проекта в реальный кри- сталл лабораторной установки и сличив наблюдаемую осцилло- грамму выхода z (Y 1, Y 2) с полученной временной диаграммой.

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

1. Изучить описание лабораторной работы.

2. Построить по заданной функции (см. п. а варианта зада- ния) комбинационную схему на элементах И-НЕ.

 

 

 

Рис. 6.21. Временные диаграммы работы схемы с учетом фактических задержек

 

Внимание! Для инверсии переменных следует использовать отдельные элементы инверторов.

 

3. Определить для построенной схемы все статические и ло- гические состязания, т.е. определить пары наборов, переход между которыми может вызвать ошибочное переключение схемы. Найти также одну пару наборов, переход между которыми вызывает функциональное состязание.

4. Произвести синтез схемы, выполняющей ту же функцию, что и в варианте, но свободную от статических и логических состя- заний.

5. Построить асинхронную последовательностную схему на элементах И-НЕ по заданным уравнениям (см. п. б варианта до- машнего задания).

 

Внимание! Для инверсии переменных следует использовать отдельные элементы инверторов.

 

6. Составить ленту для исследуемой схемы (см. табл. 6.6).

7. Выполнить синтез схемы, выполняющей ту же функцию, что и в варианте, но свободную от критических состязаний.

8. Разработать и изобразить схему исследования ассинхрон- ных последовательностных схем с использованием макроэлементов стенда и осциллографа.

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Выполнить ввод двух вариантов комбинационной схемы в редакторе схем системы Xilinx Foundation.

2. Исследовать моделированием процесс переключения ком- бинационных схем при переходах между всеми найденными пара-

 

ми входных наборов. Моделирование выполнить в режиме Unit,

учитывающем единичные задержки элементов.

3. Показать преподавателю на экране дисплея работу схем на найденных переходах.

4. Выполнить на новом листе ввод двух вариантов последо- вательностной схемы, подсоединив к её входам макроэлементы генератора тестовой последовательности сигналов х 1, х 2.

5. Выполнить в режиме моделирования с учетом единичных

задержек элементов Unit анализ переходов введенных схем.

6. Показать преподавателю полученные временные диаграм- мы работы введенных схем.

7. Выполнить размещение проекта на кристалл, предвари- тельно удалив из проекта лист с ранее введенными комбинацион- ными схемами и подсоединив к анализируемым схемам макроэле- менты лабораторной установки.

8. Выполнить временное моделирование и анализ переходов асинхронных схем.

9. Показать преподавателю полученные временные диаграм- мы работы введенных схем.

10. Выполнить загрузку проекта в ПЛИС стенда.

11. Продемонстрировать преподавателю работу схем на экране виртуального осциллографа.

12. Сдать преподавателю оформленный отчет в конце занятия.

 

ОТЧЕТ ПО РАБОТЕ

Отчет должен содержать:

1) комбинационную схему, построенную по функции, задан- ной в варианте;

2) этап определения состязаний в комбинационной схеме;

 

3) синтез комбинационной схемы, свободной от статических и логических состязаний, и саму схему;

4) асинхронную последовательностную схему, построенную по уравнениям заданным в варианте;

5) ленту для последовательностной схемы;

6) синтез последовательностной схемы, свободной от состя- заний, и саму схему;

7) схему исследования асинхронных последовательностных схем с использованием макроэлементов стенда и осциллографа.

 

Список литературы

1. Ковригин Б.Н. Триггерные схемы. Ч. 2. Синтез и анализ. М.: МИФИ, 1977.

2. Ангер С. Асинхронные последовательностные схемы. М.: Наука, 1977.

3. Фридман А., Менон П. Теория и проектирование переклю- чательных схем. М.: Мир, 1978.

4. Миллер Р. Теория переключательных схем. Т. 2. Последо- вательностные схемы и машины. М.: Наука, 1971.

5. Мак-Класки Э. Дж. Переходные процессы в комбинацион- ных логических схемах. В кн.: Методы введения избыточности для вычислительных систем. / Под ред. Пугачева В.С. М.: Сов. радио, 1966.

 

Приложение 1

БИБЛИОТЕЧНЫЕ ЭЛЕМЕНТЫ СХЕМНОГО РЕДАКТОРА

Данное приложение содержит краткие сведения по тем функ- циональным группам библиотечных элементов, которые использу- ются при выполнении лабораторного практикума по курсу «Схемо- техника ЭВМ».

 

Логические элементы

Расшифровка обозначений элементов этой группы достаточно проста, поскольку тип элемента явно указан в его названии, а число обозначает количество входов. Кроме того, у элементов некоторые входы могут быть проинвертированы, что отмечается символом B в обозначении элемента. Пример соглашения, принятого для обозна- чения логических элементов, приведен на рис. П1.1.

 

Рис. П1.1. Обозначение логических элементов

Рис. П1.2. Условное графическое

обозначение инвертора

 

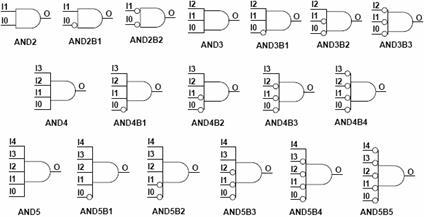
Инвертор НЕ (INV)

Условное графическое обозначение инвертора приведено на рис. П1.2.

Элементы И (AND)

Условные графические обозначения элементов AND приведены на рис. П1.3. Элементы AND до 5 входов включительно являются базовыми элементами и могут иметь инверсные входы в любой комбинации (см. рис. П1.3).

Элементы AND с числом входов от 6 до 9 не имеют инверсных входов и являются макроэлементами.

 

Рис. П1.3. Условное графическое обозначение элементов AND

 

Элементы ИЛИ (OR)

Условные графические обозначения элементов OR приведены на рис. П1.4. Элементы OR до 5 входов включительно являются базовыми элементами и могут иметь инверсные входы в любой комбинации (см. рис. П1.4).

Элементы OR с числом входов от 6 до 9 не имеют инверсных входов и являются макроэлементами.

 

 

Рис. П1.4. Условное графическое обозначение элементов OR

 

Элементы ИНЕ (NAND)

Условные графические обозначения элементов NAND приведе- ны на рис. П1.5. Элементы NAND до 5 входов включительно явля- ются базовыми элементами и могут иметь инверсные входы в лю- бой комбинации.

Рис. П1.5. Условное графическое обозначение элементов NAND

 

Элементы ИЛИ-НЕ (NOR)

Условные графические обозначения элементов NOR приведены на рис. П1.6. Элементы NOR до 5 входов включительно являются

базовыми элементами и могут иметь инверсные входы в любой комбинации (см. рис. П1.6).

Элементы NOR с числом входов от 6 до 9 не имеют инверсных входов и являются макроэлементами.

Рис. П1.6. Условное графическое обозначение элементов NOR

 

Элементы 2-2И-2ИЛИ (SOP4)

Условные графические обозначения элементов SOP4 приведены на рис. П1.7. Элементы SOP4 являются макроэлементами и могут иметь инверсные входы в любой комбинации (см. рис. П1.7).

Рис. П1.7. Условное графическое обозначение элементов SOP4

Элементы 1-2И-2ИЛИ (SOP3)

Условные графические обозначения элементов SOP3 приведены на рис. П1.8. Элементы SOP3 являются макроэлементами и могут иметь инверсные входы в любой комбинации (см. рис. П1.8).

Рис. П1.8. Условное графическое обозначение элементов SOP3