
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез комбинационных многовыходных схемСодержание книги
Поиск на нашем сайте
На практике относительно редко встречаются комбинационные схемы с одним выходом, т.е. реализующие одну функцию. Обычно схемы имеют несколько выходов, причем значения сигналов на всех выходах зависят от одних и тех же входных сигналов. Работа комбинационной схемы, имеющей п входов и k выходов, описыва- ется совокупностью k функций (2.1), каждая из которых определяет закон функционирования схемы по одному выходу. Если провести минимизацию переключательных функций, вхо- дящих в совокупность, независимо друг от друга, то схема с мно- гими выходами, реализующая эти функции, будет содержать k изо- лированных цепей. Однако в общем случае схему можно сущест- венно упростить за счет объединения участков схемы, реализую- щих одинаковые члены (или группы членов), содержащиеся в не- скольких переключательных функциях. Например, реализация двух функций в МДНФ
потребует применения четырех элементов И и двух элементов ИЛИ. Если же первую из них представить в виде
то, отказываясь от минимального представления, но не изменяя значения функции (это легко проверить, например, по диаграмме Вейча), можно упростить реализацию, поскольку первый член яв- ляется общим для обеих функций. В этом случае потребуется три элемента И и два элемента ИЛИ.
Общая идея минимизации схем с многими выходами сводится к получению таких выражений для совокупности переключательных функций, в которых оптимально используются члены, общие для нескольких функций. Минимизация системы логических функций Рассмотрим один из методов совместной минимизации системы логических функций — метод меток [1-4]. Данный метод предусматривает выполнение следующих этапов: • нахождение всех простых импликант системы логических функций; • определение простых импликант для минимального пред- ставления системы логических функций; • запись каждой логической функции в дизъюнктивной нор- мальной форме. Нахождение всех простых импликант системы логических Функций Пусть даны три функции, каждая из которых зависит от четырех переменных:
F 2 (A, B, C, D) = å (2, 3,10), ⎪ (2.4)
Таким образом, сначала находят все простые импликанты каж- дой функции системы F 1, F 2, F 3. Затем из функций системы обра- зуют все возможные подсистемы, состоящие из двух функций: F 1× F 2, F 1· F 3, F 2· F 3. Для каждой из полученных подсистем функций находят все простые импликанты. Затем образуют подсистему из трех функций F 1· F 2· F 3 и для нее находят все простые импликанты. Эту процедуру удобнее всего выполнить, используя диаграм- мы Вейча. Занесем исходные функции на три диаграммы Вейча (рис. 2.4).
Рис. 2.4. Диаграммы Вейча трех функций Найдем все простые импликанты для этих функций, т.е. сокра- щенную дизъюнктивную нормальную форму (СкДНФ) функций F 1, F 2, F 3:
F 1 = BD Ú CD Ú AD,⎫
F 2 = BCD Ú ABC, ⎬
(2.5)
Затем необходимо найти СкДНФ функций, представляющих со- бой все сочетания логических произведений исходных функций: F 1· F 2, F 1· F 3, F 2· F 3 и F 1· F 2· F 3. Получение логического произведения функций легко осущест- вить с помощью диаграммы Вейча. Для этого необходимо совмес- тить диаграммы Вейча соответствующих функций. Затем в каждой клетке совмещенной диаграммы выполнить операцию конъюнкция над значениями совмещаемых функций. Данная операция показана на рис. 2.5 для функции F 1· F 2. На этом же рисунке представлены диаграммы Вейча и для ос- тальных логических произведений исходных функций.
По полученным диаграммам найдем простые импликанты дан- ных функций: F 1 × F 2 = BCD, ⎫ F × F = ABD, ⎪
1 3 ⎪ (2.6)
F 2 × F 3 = ABC,
Рис. 2.5. Диаграммы Вейча логических произведений трех функций
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.46.174 (0.008 с.) |






 f 1 = x 1 x 2 x 3 Ú x 1 x 2,
f 1 = x 1 x 2 x 3 Ú x 1 x 2, Из этого примера следует, что задача минимизации для системы переключательных функций не может быть сведена к задаче минимизации отдельных функций.
Из этого примера следует, что задача минимизации для системы переключательных функций не может быть сведена к задаче минимизации отдельных функций. Простые импликанты системы логических функций (2.4) представляют собой совокупность простых импликант всех сочетаний логических произведений исходных функций, включая и функции системы: F 1, F 2, F 3, F 1× F 2, F 1· F3, F 2· F 3 и F 1 ·F 2 ·F 3.
Простые импликанты системы логических функций (2.4) представляют собой совокупность простых импликант всех сочетаний логических произведений исходных функций, включая и функции системы: F 1, F 2, F 3, F 1× F 2, F 1· F3, F 2· F 3 и F 1 ·F 2 ·F 3.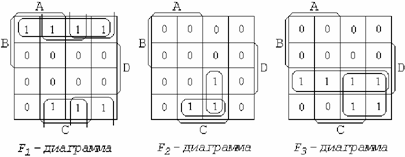



 ⎪
⎪









