Построение асинхронной схемы на заданной системе элементов

Представим полученные выражения в базисе Шеффера:

 

Y 1 = (⎯x 1 | x 2) | (⎯ x 1 |⎯ y 2) | (x 2 | y 1),

Y 2 = (⎯ x 1 | x 2) | (⎯x 1 | y 2) |(x 2 |⎯ y 1),

z = y 2.

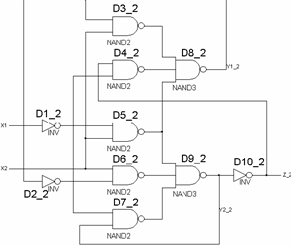
Затем по данным выражениям построим комбинационную схе- му на элементах И-НЕ, после чего соединим ее одноименные по- люса (вход y — выход Y), т.е. образуем обратные связи (рис. 6.16). В результате получим структуру асинхронной последовательност- ной схемы, свободной от критических состязаний.

 

 

Рис. 6.16. Cхема, свободная от критических состязаний сигналов

 

Изложенный материал далеко не исчерпывает всех проблем, связанных с состязаниями в цифровых схемах, однако может по- мочь во многих случаях обнаружить состязания и принять меры по их устранению.

ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ СОСТЯЗАНИЙ СИГНАЛОВ

Экспериментальное исследование состязаний сигналов в цифро- вых схемах проводится как с помощью моделирования, так и на универсальном лабораторном стенде.

 

Исследование комбинационной схемы

Исследование состязаний сигналов в комбинационной схеме выполняется только моделированием с использованием единичных задержек элементов. Для этого необходимо задать на входах ком- бинационной схемы переходы между всеми парами состояний, вы- зывающих состязания сигналов.

Исследование последовательностной схемы

Для исследования состязаний сигналов в последовательностной схеме необходимо подать на ее вход полную последовательность смежных входных состояний x 1 ,x 2: 00 ® 01 ® 11 ® 10 ® 00 ®

10 ® 11 ® 01 ® 00 и т.д.

Данную последовательность вырабатывает схема, изображен- ная на рис. 6.17. Временная диаграмма ее работы приведена на рис. 6.18.

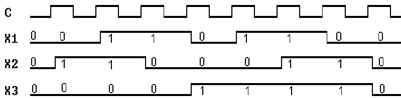
Рис. 6.17. Генератор последовательности смежных состояний х 1, х 2

 

Рис. 6.18. Временная диаграмма генератора последовательности смежных состояний х 1, х 2

Схема генератора тестовой последовательности сигналов х 1, х 2 оформлена в виде макроэлемента, условное графическое обозначе- ние которой приведено на рис. 6.19. Данный макроэлемент содер- жится в библиотеке проекта maket.

Доступность выходного сигнала Х 3 макроэлемента облегчает выделение периода работы исследуемой схемы на временной диа- грамме при моделировании, а также данный сигнал необходим для синхронизации осциллографа при выполнении эксперимента на лабораторном стенде.

 

 

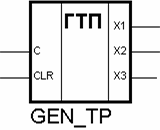
Рис. 6.19. Условное графическое обозначение генератора тестовой последовательности смежных состояний х 1, х 2

 

Исследование заданной асинхронной схемы выполняют как мо- делированием в САПР Xilinx, так и на универсальном лаборатор- ном стенде.

 

Построение ленты схемы

С целью фиксации ошибочного перехода исследуемой схемы из-за состязаний сигналов необходимо заранее по таблице перехо- дов и выхода определить реакцию схемы на заданную полную по- следовательность смежных входных состояний (см. рис. 6.18).

В табл. 6.6 приведена заданная последовательность входных сигналов и соответствующие ей последовательности состояний внутренних переменных и выхода для схемы рис. 6.9. Закон функ- ционирования этой схемы определен табл. 6.1. Табл. 6.6 называют лентой схемы. Ленту схемы строят по кодированной таблице пере-

ходов (см. табл. 6.1), определяя возможные переходы при измене- нии входного состояния.

После включения питания и установки в нулевое состояние ге- нератора последовательности x 1 ,x 2 исследуемая схема может ока- заться в одном из двух устойчивых состояний y 1 y 2 z = 101 или y 1 y 2 z = 110 (см. табл. 6.1). При составлении табл. 6.6 за начальное принято состояние схемы y 1 y 2 z = 1ХХ.

Из табл. 6.1 определяем переходы с критическими состязаниями и фиксируем в табл. 6.6 возможные ошибочные переходы.

Для рассматриваемого примера схема из ошибочного состояния вновь переходит в русло правильной работы (см. табл. 6.1). В об- щем случае после ошибочного перехода последовательность со- стояний схемы может отличаться от правильной. В этом случае в ленте фиксируют как правильную последовательность состояний схемы, так и последовательность состояний после ошибочного пе- рехода.

Как видно из табл. 6.6, после первого завершения периода вход- ной последовательности схема переходит в состояние y 1 y 2 z = 110, которое отлично от исходного состояния y 1 y 2 z = 1ХХ01. Поэтому необходимо продолжить построение ленты исследуемой схемы до выделения периода работы схемы. Это необходимо для исследова- ния работы схемы в динамическом режиме.

Поскольку после второго периода входной последовательности схема переходит в состояние y 1 y 2 z = 110, т.е. совпадает с состояни- ем схемы в начале этого периода, то построение ленты можно за- вершить (см. табл. 6.6).

 

Таблица 6.6