
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое натуральное число? Как обозначается множество натуральных чисел?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Числовые системы Что такое натуральное число? Как обозначается множество натуральных чисел? Натуральные числа – это абстрактные объекты, при помощи которых описываются конечные множества отдельных предметов. Натуральное число является общей характеристикой всех мыслимых конечных множеств, между элементами которых можно установить взаимно-однозначное соответствие. Если между элементами двух конечных множеств невозможно установить взаимно-однозначное соответствие, то этим множествам соответствуют отличные натуральные числа. Обозначаются натуральные числа буквой N.:
Что такое число НОЛЬ Число ноль - это такое число, которое характеризует ситуацию? когда в рассматриваемом множестве нет элементов. Как определяется операция сложения натуральных чисел? Сложение натуральных чисел определяется исходя из смысла натуральных чисел. Если имеются два натуральных числа, то им соответствуют какие-то множества отдельных предметов. Натуральное число, описывающее множество отдельных предметов, состоящее из элементов обоих данных множеств и называется суммой двух, начально взятых натуральных чисел.
Как определяется операция вычитания натуральных чисел? Вычитание натуральных чисел можно определить двумя способами: первый способ (естественный) - определение производится как и в случае сложения исходя из смысла натуральных чисел. Вычитание натуральных чисел отражает идею изъятия части элементов какого-нибудь конечного множества из множества всех его элементов. Как видно из этого описания операции вычитания, она выполнима не всегда. Второй способ (формально – логический) – определение производится строго формально. Операция вычитания в этом случае определяется как обратная операция для операции сложения. Какие свойства операции сложения можно наблюдать исходя непосредственно из смысла натуральных чисел и смысла операции сложения смысла? Такими свойствами являются: 1 - переместительность (коммутативность) n + m = m + n, слагаемые можно ставить в любом порядке 2 - сочетательность (ассоциативность) (n + m) + k = m + (n + k), слагаемые можно разбивать на группы любым способом 3 - свойство нуля n + 0 = n при прибавлении к любому числу нуля сумма будет равна тому же числу Можно ли математически доказать коммутативность, ассоциативность сложения и свойство нуля по отношению к сложению? Убедиться в справедливости этих свойств возможно только из смысла натуральных чисел и операции сложения. Доказать эти свойства опираясь на некоторые, более простые утверждения нельзя. Как определяется операция умножения натуральных чисел? Можно ли сказать, что операция умножения является логической конструкцией изготовленной Можно ли сказать, что числа участвующие в операции умножения имеют одинаковый смысл, как это имеет место при операции сложения? ВОПРОСЫ ДЕЛИМОСТИ
Что такое простое число? Число называется простым если оно не имеет делителей, отличных от единицы и самого себя. ЦЕЛЫЕ ЧИСЛА РАЦИОНАЛЬНЫЕ ЧИСЛА При переходе от натуральных чисел к целым основные свойства неравенств получили определенные изменения (дополнения). Изменились ли основные свойства неравенств при переходе от целых чисел к рациональным? При переходе от натуральных чисел к целым добавились отрицательные числа, для которых, в отличии от натуральных, чем больше модуль числа, тем меньше само число. Именно это обстоятельство и привело к дополнениям в основных свойствах неравенств. При переходе от целых к рациональным, новых объектов с подобными свойствами введено не было. Поэтому основные свойства неравенств на рациональных числах точно такие же как они сформулированы для целых чисел.
ПРОЦЕНТЫ ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
Рассматривая эволюцию числовых систем от N до Z, и затем до Q видно, что с формальной точки зрения, каждая последующая система устраняла неполноту какой-нибудь из обратных операций: при переходе от N к Z- устранялась неполнота операции вычитания, при переходе от Z к Q – устранялась неполнота операции деления. Можно ли сказать, что переход от Q к R устранил неполноту некоторой обратной операции? Да, таки и было. Была устранена неполнота операции извлечения корней любых натуральных степеней из положительных рациональных чисел.
КОМПЛЕКСНЫЕ ЧИСЛА.
Каков смысл символа i? Никакого, кроме того, что это формальный объект, обладающий определенными свойствами относительно арифметических операций.
В чем отличие дробного рационального выражения от рациональной дроби? Пример? Дробное рациональное выражение- это любое выражение с переменными содержащее хотя бы одну переменную хотя бы в одном делителе. Рациональная дробь – это такое дробное рациональное выражение, в котором существует только один делитель содержащий переменную(ые) и этот делитель является многочленом.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ.
Что называется тождеством? Тождеством называется равенство по обе стороны которого стоят тождественные выражения.
148. Что называется тождественным преобразованием данного алгебраического выражения? Переход от одного алгебраического выражения к другому, но тождественно ему равному называется тождественным преобразованием.
149. С какой целью выполняются тождественные преобразования алгебраических выражений? Алгебраические выражения возникающие в ходе решения каких-либо задач или построения математических моделей каких-нибудь явлений (в любой области деятельности) часто имеют громоздкий, неуклюжий, трудночитаемый вид. В этих случаях, возникает понятное желание сделать выражение проще, но так, чтобы оно осталось тождественно равным исходному. Более простое выражение, например, быстрее, удобнее и точнее можно вычислить. С другой стороны, если выражение является моделью некоторого явления, другая, но тождественная форма этого выражения может помочь увидеть такие свойства явления, которые невозможно увидеть в другом представлении.
150. Трудно ли производить тождественные преобразования? Умение производить тождественные преобразования алгебраических, а в дальнейшем и не только алгебраических выражений является очень важным моментом в применении математики как для прикладных целей, так и для решения внутренних, чисто математических задач. Техника преобразований математических выражений может быть весьма изощренной и представлять собой определенное искусство. Важным арсеналом технических инструментов для таких преобразований являются уже известные формы представлений или формулы. Чем больше формул и представлений известно, тем более вероятно, что будет найдено требуемое преобразование. Вот почему необходимо помнить некоторые базовые формулы в математике. Школьная программа предусматривает довольно большой набор простых, но важных соотношений и приемов, при помощи которых производятся различные преобразования математических выражений. Для успешного применения математики нужно не только хорошее владение математическими понятиями и определениями, но и хорошая техническая вооруженность, которая проявляется в знании и владениями определенными приемами и методами, техникой алгебраических преобразований в том числе. Вообще же, часто, увидеть, возможность того или иного преобразования дело не только знаний и технической оснащенности математика, но и его способностей или таланта, как например, в шахматах – оба шахматиста хорошо знают правила игры в шахматы и могут обладать одинаковым набором технических приемов игры, тем не менее, выигрывает один из них. ------------------------------------------------------------------------------------------------------- Числовые системы Что такое натуральное число? Как обозначается множество натуральных чисел? Натуральные числа – это абстрактные объекты, при помощи которых описываются конечные множества отдельных предметов. Натуральное число является общей характеристикой всех мыслимых конечных множеств, между элементами которых можно установить взаимно-однозначное соответствие. Если между элементами двух конечных множеств невозможно установить взаимно-однозначное соответствие, то этим множествам соответствуют отличные натуральные числа. Обозначаются натуральные числа буквой N.:
Что такое число НОЛЬ Число ноль - это такое число, которое характеризует ситуацию? когда в рассматриваемом множестве нет элементов.
|
||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.119 (0.008 с.) |

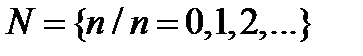 или
или 
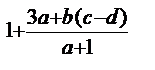 - дробное рациональное выражение, но не рациональная дробь.
- дробное рациональное выражение, но не рациональная дробь.  - тоже дробное рациональное выражение, но не рациональная дробь (потому, что в числителе не многочлен).
- тоже дробное рациональное выражение, но не рациональная дробь (потому, что в числителе не многочлен).  -- рациональная дробь, так как и в числителе и в знаменателе многочлены.
-- рациональная дробь, так как и в числителе и в знаменателе многочлены.


