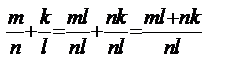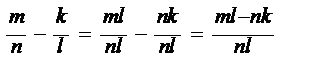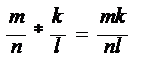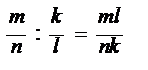В каких случаях возникает необходимость приведения дробей к общему знаменателю?

Пользуясь основным свойством дроби любые две обыкновенные дроби можно привести к виду, когда они имеют общий знаменатель. Дроби имеющие общий знаменатель можно складывать, вычитать и сравнивать между собой. Таким образом всякий раз, когда надо совершить одну из этих операций необходимо привести дроби к общему знаменателю.

 

Каковы правила арифметических операция для рациональных чисел в форме дробей?

Правила арифметических операций для рациональных чисел, представленных в форме обыкновенных дробей следующие:

1 – чтобы сложить две дроби надо привести их к общему знаменателю и после этого составить дробь у которой числитель сумма числителей, а

знаменатель -общий:

2 – чтобы вычесть одну дробь из другой надо привести их к общему знаменателю и после этого составить дробь у которой числитель разность

числителей, а знаменатель –общий:

3 – чтобы умножить одну дробь на другую надо составить дробь у которой числитель произведение числителей, а знаменатель – произведение

Знаменателей:

4 – чтобы разделить одну дробь на другую надо составить дробь у которой числитель произведение числителя делимой дроби на знаменатель

дроби делителя, а знаменатель – произведение знаменателя делимой дроби на числитель дроби-делителя:

Как умножить дробь на целое число? Как разделить дробь целое на число?

Чтобы умножить дробь на число надо умножить на это число числитель, а знаменатель оставить без изменения.

Чтобы разделить дробь на целое число надо умножить на это число знаменатель, а числитель оставить без изменения.

 

Как сравнить два рациональных числа в виде дробей?

Надо привести дроби к общему знаменателю и сравнить числители.

 

Какой порядок на рациональных числах считается естественным?

Порядок на рациональных числах полученный путем продолжения естественного порядка целых чисел и при котором сравнение рациональных чисел происходит по правилу 55 считается естественным порядком на рациональных числах.

 

При переходе от натуральных чисел к целым основные свойства неравенств получили определенные изменения (дополнения). Изменились ли основные свойства неравенств при переходе от целых чисел к рациональным?

При переходе от натуральных чисел к целым добавились отрицательные числа, для которых, в отличии от натуральных, чем больше модуль числа, тем меньше само число. Именно это обстоятельство и привело к дополнениям в основных свойствах неравенств. При переходе от целых к рациональным, новых объектов с подобными свойствами введено не было. Поэтому основные свойства неравенств на рациональных числах точно такие же как они сформулированы для целых чисел.