Как определяется умножение одночленов и возведение одночлена в степень.

Умножение и возведение в степень одночленов определяется исходя из смысла этих операций. Чтобы найти произведение одночлена на одночлен находят коэффициент, как произведение коэффициентов исходных одночленов, затем используя коммутативность и ассоциативность умножения последовательно собирают вместе одинаковые переменные в различных степенях и представляют их одной переменной в суммарной степени. Таким образом получается стандартный вид одночлена - произведения.

 

Какое (рациональное) выражение называется многочленом?

Произвольная сумма одночленов называется многочленом.

Какие элементы многочлена называются подобными? Что означает выражение «привести подобные»?

Одночлены, входящие в состав многочлена в качестве слагаемых, называются подобными, если они отличаются только коэффициентом. Приведение подобных в многочлене- это операция нахождения всех подобных одночленов и замена их одним из них, но с коэффициентом, равным сумме коэффициентов всех подобных одночленов.

 

Какие операции можно совершать с многочленами?

Многочлены можно складывать и вычитать, умножать друг на друга (используется распределительный закон умножения относительно сложения). Кроме того, многочлены можно делить один на другой с остатком. Теорема о делении многочленов с остатком звучит точно так же как основная теорема арифметики, делении любого натурального числа на любое с остатком. В случае деления многочленов единственность частного и остатка сохраняется. Процедура деления одного многочлена на другой не более сложная, чем деление с остатком одного натурального числа на другое.

 

142. Какое выражение называется рациональной дробью? Привести примеры.

Рациональной дробью называется дробное выражение, у которого числитель и знаменатель – многочлены.

 

В чем отличие дробного рационального выражения от рациональной дроби? Пример?

Дробное рациональное выражение- это любое выражение с переменными содержащее хотя бы одну переменную хотя бы в одном делителе.

Рациональная дробь – это такое дробное рациональное выражение, в котором существует только один делитель содержащий переменную(ые) и этот делитель является многочленом.

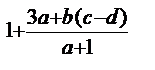- дробное рациональное выражение, но не рациональная дробь. - тоже дробное рациональное выражение, но не рациональная дробь (потому, что в числителе не многочлен). -- рациональная дробь, так как и в числителе и в знаменателе многочлены.