
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В чем состоит основное свойство рациональной дроби?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основное свойство рациональной дроби состоит в том, что если числитель и знаменатель умножить или разделить на один и тот же, не равный нулю, многочлен, то полученная рациональная дробь будет равна исходной. Или по-другому – Если числитель и знаменатель рациональной дроби умножить или разделить на один и тот же ненулевой многочлен, то дробь не изменится.
Каким образом производятся арифметические операции или действия с рациональными дробями? Основное свойство рациональной дроби звучит точно так же, как и основное свойство обыкновенной числовой дроби. Поэтому арифметические операции с рациональными дробями или над рациональными дробями производятся точно так же, как и над обыкновенными числовыми дробями. ТОЖДЕСТВЕННЫЕ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ И ИХ КЛАССИФИКАЦИЯ. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ.
Какие два выражения с переменными или алгебраических выражения называются тождественно равными? Два алгебраических выражения называются тождественно равными, если они имеют одинаковые области допустимых значений и равны между собой при всех допустимых значениях переменных. Например: выражения
Что называется тождеством? Тождеством называется равенство по обе стороны которого стоят тождественные выражения.
148. Что называется тождественным преобразованием данного алгебраического выражения? Переход от одного алгебраического выражения к другому, но тождественно ему равному называется тождественным преобразованием.
149. С какой целью выполняются тождественные преобразования алгебраических выражений? Алгебраические выражения возникающие в ходе решения каких-либо задач или построения математических моделей каких-нибудь явлений (в любой области деятельности) часто имеют громоздкий, неуклюжий, трудночитаемый вид. В этих случаях, возникает понятное желание сделать выражение проще, но так, чтобы оно осталось тождественно равным исходному. Более простое выражение, например, быстрее, удобнее и точнее можно вычислить. С другой стороны, если выражение является моделью некоторого явления, другая, но тождественная форма этого выражения может помочь увидеть такие свойства явления, которые невозможно увидеть в другом представлении.
150. Трудно ли производить тождественные преобразования? Умение производить тождественные преобразования алгебраических, а в дальнейшем и не только алгебраических выражений является очень важным моментом в применении математики как для прикладных целей, так и для решения внутренних, чисто математических задач. Техника преобразований математических выражений может быть весьма изощренной и представлять собой определенное искусство. Важным арсеналом технических инструментов для таких преобразований являются уже известные формы представлений или формулы. Чем больше формул и представлений известно, тем более вероятно, что будет найдено требуемое преобразование. Вот почему необходимо помнить некоторые базовые формулы в математике. Школьная программа предусматривает довольно большой набор простых, но важных соотношений и приемов, при помощи которых производятся различные преобразования математических выражений. Для успешного применения математики нужно не только хорошее владение математическими понятиями и определениями, но и хорошая техническая вооруженность, которая проявляется в знании и владениями определенными приемами и методами, техникой алгебраических преобразований в том числе. Вообще же, часто, увидеть, возможность того или иного преобразования дело не только знаний и технической оснащенности математика, но и его способностей или таланта, как например, в шахматах – оба шахматиста хорошо знают правила игры в шахматы и могут обладать одинаковым набором технических приемов игры, тем не менее, выигрывает один из них. -------------------------------------------------------------------------------------------------------
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.158.84 (0.006 с.) |

 и
и  - тождественно равные. Они aимеют одинаковые ОДЗ (любые числа a и b) и их значения равны при любых значениях переменных. Выражения:
- тождественно равные. Они aимеют одинаковые ОДЗ (любые числа a и b) и их значения равны при любых значениях переменных. Выражения:  и
и 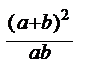 тоже тождественно равны. Их ОДЗ совпадают (хотя, на этот раз это уже не все числа) и при всех значениях из ОДЗ значения выражений совпадают. Однако, выражения
тоже тождественно равны. Их ОДЗ совпадают (хотя, на этот раз это уже не все числа) и при всех значениях из ОДЗ значения выражений совпадают. Однако, выражения  - имеют различные ОДЗ, но на общей части своих ОДЗ принимают одинаковые значения при всех значениях переменных. В этом случае говорится, что исходные выражения тождественны на определенном множестве. В данном случае рассматриваемые выражения тождественны при всех значениях а и b, кроме а=0 и b=0.
- имеют различные ОДЗ, но на общей части своих ОДЗ принимают одинаковые значения при всех значениях переменных. В этом случае говорится, что исходные выражения тождественны на определенном множестве. В данном случае рассматриваемые выражения тождественны при всех значениях а и b, кроме а=0 и b=0.


