
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какое важное изменение в свойствах неравенств произошло при переходе от натуральных чисел к целым числам.Содержание книги
Поиск на нашем сайте
Главные свойства отношения неравенства на натуральных числах показаны в вопросе 25. При переходе к целым числам свойства не касающиеся операций и касающиеся операций сложения и вычитания остаются без изменения, однако свойства 25.5 и 25.6 говорящие о сохранении неравенства при умножении и делении обеих частей на одно и то же число приобретают дополнительную особенность. И формулируются для целых чисел следующим образом: 5. Если n < m, а k – положительное число, то n * k < m * k если обе части неравенства умножить на одно и то же положительное число, то неравенство сохраниться. Исходные числа в неравенстве могут быть любыми (пол,отр). Сохранение неравенства при умножении на положительное число. Например: Здесь показаны все возможные случаи умножения неравенства на положительное число 8. Если n < m, а k – отрицательное число, то n * k > m * k если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства сменится на противоположный. Исходные числа в неравенстве, тем не менее, могут быть любыми. Смена знака неравенства на противоположный при умножении на отрицательное число. Например:
Здесь показаны все возможные случаи умножения неравенства на отрицательное число (-8). Точно так же с делением: 6. Если n < m, а k – положительное число, то n: k < m: k если обе части неравенства разделить на одно и то же положительное число, то неравенство сохраниться. Исходные числа в неравенстве любыми. Сохранение неравенства при делении на положительное число.(Если деление возможно) Например: Здесь показаны все возможные случаи деления неравенства на положительное число 6. Если n < m, а k – отрицательное число, то n: k > m: k если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства сменится на противоположный. Исходные числа в неравенстве, тем не менее, могут быть любыми. Смена знака неравенства на противоположный при делении на отрицательное число. (Если деление возможно) Например:
Здесь показаны все возможные случаи деления неравенства на отрицательное (- 6). (Неравенства для степеней (свойства 7 и 8) перестают работать на целых числах в том виде как они работают на натуральных числах. Полный перечень свойств неравенств на целых и рациональных числах целесообразно привести после строго определения степени с отрицательным и дробным показателем.)
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.50 (0.007 с.) |

 или 32 < 56,
или 32 < 56,  или -56 < -32,
или -56 < -32, 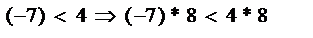 или (-56) < 32)
или (-56) < 32) или (-32) > (-56) - произошла смена знака неравенства.
или (-32) > (-56) - произошла смена знака неравенства. или 56 > 32 - произошла смена знака неравенства.
или 56 > 32 - произошла смена знака неравенства. или 56 > (-32) - произошла смена знака неравенства.
или 56 > (-32) - произошла смена знака неравенства.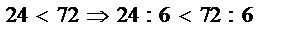 или 4 < 12,
или 4 < 12,  или -12 < -6,
или -12 < -6, 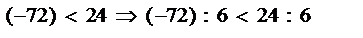 или (-12) < 4
или (-12) < 4 или (- 4) >(- 12) - произошла смена знака неравенства.
или (- 4) >(- 12) - произошла смена знака неравенства.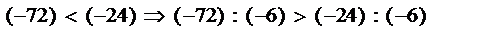 или 12 > 4 - произошла смена знака неравенства.
или 12 > 4 - произошла смена знака неравенства. или 24 > (-4) - произошла смена знака неравенства.
или 24 > (-4) - произошла смена знака неравенства.


