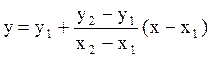Молярна електрична провідність водних розчинів

калію хлориду при 25 °С

 

Число молів	Питома електрична провідність æ, См·м^-1	Молярна електрична провідність m, См·м^2·моль^-1
в 1 л	в 1 м^3
0,1 0,01 0,001 0,0001	10^3 10^2 10^-1	11,1900 1,2890 0,1413 0,014690 0,001489	0,01119 0,01289 0,01413 0,01469 0,01489

 

Таблиця 2.

Дані для визначення константи швидкості k реакції омилення

оцтоетилового етеру в кислому середовищі при 25°С

t, c	Vt, см^3 лугу	V¥ - Vt, см^3	t – t0, c	k·10^-4,c^-1
339 = t0	26,34	13,47 = V0		-
	27,80	12,01		1,27
	29,70	10,11		1,19
	31,81	8,00		1,24
¥	39,81= V¥		¥	-

 

Іноді результати експерименту оформлюють у вигляді так званного висновку, тобто двопараметричної таблиці. Наприклад:

Таблиця 3.

Густина розчинів фосфорної кислоти у воді при 20 °С.

Концентрація Н3Р04, %
Густина, кг/м^3	998,2	1053,2	1113,4	1180,5	1254,0

 

 

При округленні чисел слід дотримуватися наступних правил:

- якщо перша цифра, що відкидається, менше п'яти, то останню цифру залишають незмінною (12,345 округляють до 12,3);

- якщо перша цифра, що відкидається, більше чи дорівнює п'яти, а наступні цифри більше нуля, то останню цифру збільшують на одиницю (12,367 округляють до 12,4; 12,352—до 12,4);

- якщо цифра, що відкидається, дорівнює п'яти, і за нею випливають тільки нулі, то число округляють до найближчого парного значення (12,350 округляють до 12,4; 12,450 - до 12,4).

У всіх цих прикладах передбачалося, що сумнівною є перша цифра за комою.

В цілих числах цифри, що випливають за першою сумнівною, замінюють нулями (наприклад, швидкість світла у вакуумі n = 299 792 500 м/с).

Інтерполяцією називають визначення значення функції, що знаходиться між виміряними її значеннями; вона може бути аналітичною чи графічною.

Тоді, коли без великої похибки можна вважати, що функція у лінійно змінюється між двома сусідніми значеннями х, для інтерполяції використовують метод пропорційних частин. Функцію у, що відповідає даному значенню аргументу х, що лежить між двома табличними значеннями x₁, у₁ і х₂, у₂ обчислюють за формулою:

У загальному випадку слід скласти емпіричне рівняння у = f(x) за виміряним значенням у і по цьому рівнянню обчислити шукане значення у.

Досить часто використовують надійний графічний спосіб. За табличними даними креслять на міліметровому папері криву у= f (х) у масштабі, що дозволяє врахувати останню значущу цифру вимірюваної величини. По кривій знаходять значення у, що відповідає будь-якому значенню х.

Екстраполяцією називають значення у, яке відповідає деякому х, щолежить поза межами досліджених даних; екстраполяція може бути аналітичною і графічною. Точність екстраполяції (особливо при значному її інтервалі) невелика, однак, у деяких випадках постулюють чи теоретично обґрунтовують застосування цього способу.

Побудова графіків

Графічне зображення експериментальних і розрахункових даних полегшує порівняння величин, дозволяє легко знайти характер зміни величин — наяв­ність екстремальних точок чи точок перегину, періодичність, поява граничних зна­чень та інші важливі властивості. У таблицях ці особливості виявляються менш чітко. Нарешті, за допомогою графіків можна робити диференціювання й інтег­рування, навіть не знаючи математичної форми представленої графічної залеж­ності.

При побудові графіків необхідно дотримуватись наступних правил.

Значення незалежної змінної (аргументу) відкладають по осі абсцис, функ­ції - по осі ординат. Яку з двох змінних вважати незалежною, випливає звичай­но з експерименту. Якщо, в ході досліду значення однієї змінної встановлюють довільно, а відповідні значення інших змінних виявляються при цьому цілком визначеними, то перша змінна і вважається незалежною. Загального правила для вибору аргументу не існує.

В и б і р м а с ш т а б у.

І. Масштаб потрібно обирати так, щоб координати будь-якої точки графіка могли бути визначені швидко і легко. Якщо на розграфленому в клітинку папері (міліметровому) відстань між двома головними сусідніми лініями розділено на десять рівних частин, то найбільш зручно вибирати такий масштаб, при якому ця відстань прийнята за 1, 2 чи 5 одиниць, або за ці значенняпомножені на 10^{± n}, де n — ціле число. Масштаб, при якому читання графіка утруднене, не може вважатися прийнятним (порівняйте рис.1 а і 1 б, що є прикладами зручного і незручного вибору масштабів).

Не всі лінії координатної сітки повинні бути надписані; часто для читання графіка виявляється зручним надписувати лінії через одну.

Рис. 1. Залежність логарифма тиску насиченої пари дифенілу від зворотної температури, побудована у (а) правильно і (б) неправильно вибраних масштабах.

 

Але яка б система надпису позначень не була прийнята, вона повинна бути дотримана на всьому графіку. Доцільно, щоб числа, проставлені на осі, містили стільки значущих цифр, скільки допускає точність даних чи скільки можна прочитати по кривій (рис.1а). Для зручності користування графіком необхідно проставити на кожній координатній осі назву величини, що представляється нею, і одиниць, у яких вона вимірюється.

 

 

 

Рис. 2 Залежність питомої провідності соляної кислоти від

концентрації, побудована в (а) правильно і (б) неправильно вибраних масштабах

 

II. Масштаб слід обирати так, щоб похибка вимірювань відповідала похибці на графіку не більш, ніж в одну-дві найменших поділок масштабу. При виборі шкали по осі координат немає необхідності обов'язково починати з нульового значення, якщо це не викликано спеціальними міркуваннями (необхідність екстраполяції і т.п.). Відповідно до цього правила, шкала для кожної змінної може починатися з найменшого округленого значення із сукупності даних чи трохи нижче і закінчуватися найбільшим округленим значенням чи трохи вище (рис.2).

III. Якщо графік використовують для визначення коефіцієнтів рівняння, що виражає залежність у = f(x),або для екстраполяції отриманої залежності, варто вибирати таку функціональну залежність, при якій зменшується кривизна ліній (звичайну логарифмічну, показову з дробовим показником ступеня та ін.).

IV. Масштаб повинен бути обраний так, щоб крива, наскільки це можливо, була нахилена до осі абсцис під кутом, близьким до 45°.

При необхідності підкреслити характерні риси в зміні функції (наявність екстремальних точок, точок перегину і т.п.) варто відносно збільшити масштаб функції і зменшити масштаб аргументу (рис. 2 а і 2 б; максимум питомої електропровідності в першому випадку виражений більш чітко).