
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ДС.2 Використання теореми про зміну кінетичного моменту для дослідження руху матеріальної системиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Матеріальна система (рис. 2.1-2.5) приводиться до руху моментом М, що прикладений до однорідного тіла 3. Знайти закон руху тіла 1, якщо на тіло 2 діє постійний момент опору М оп. В початковий момент часу кутова швидкість тіла 3 - w30. Масами пасів та їх ковзанням по шківах знехтувати. Тіла 2 та 3, обертаються навколо горизонтальних осей. Дані для розрахунку приведені в таблиці 2.1. Де R2, r2, R3 – розміри тіла 2 та 3, і2 – момент інерції тіла 2 відносно осі обертання, m1, m2, m3 – маси тіл 1, 2 та 3.
Таблиця 2.1
Рисунок 2.1
Рисунок 2.4
Рисунок 2.5
Приклад виконання завдання
До вантажу 1 (рис. 2.6) масою m1=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом r2 (m2=2кг). Механічна система приводиться до руху моментом Знайти закон руху вантажу 1, якщо на тіло 2 діє момент опору МОП = 15 Н×м і при t=0 кутова швидкість тіла 3 -
Рисунок 2.6
Розв’язання. Розглянемо окремо рух тіл 2 і 3 та рух тіл 1 і 4. До тіла 3 (рис. 2.7) прикладені зовнішні сили: пара сил з моментом М, сила тяжіння P3=m3g, реакції циліндричного шарніра X3 і Y3, реакції тіла 2 – колове зусилля S3 і сила нормального тиску N3. Запишемо диференціальне рівняння обертання тіла 3 навколо нерухомої осі враховуючи, що якщо момент зовнішніх сил діє у напрямку руху тіла, тоді записуємо його з додатним знаком.
де
Рисунок 2.7
Початкові умови: при t=0, На тіло 2 діють такі зовнішні сили: сила тяжіння P2=m2g, реакції циліндричного шарніра X2 та Y2, натяг троса S2 (трос працює тільки на розтяг), реакції тіла 3 – Диференціальне рівняння обертання тіла 2 (рис. 2.8) навколо горизонтальної осі Z.
де Оскільки
До тіл 1 та 4 (рис. 2.9) прикладені зовнішні сили: сили тяжіння P1=m1g та P4=m4g, реакція троса
Рисунок 2.8
Теорема про зміну кінетичного моменту для тіл 1 та 4 (рис. 2.9) в проекціях на вісь Z запишеться:
Рисунок 2.9
де lZ – кінетичний момент системи тіл 1 та 4 відносно осі Z, Кінетичний момент LZ складається із моменту кількості руху LZ1 тіла 1 та кінетичного моменту LZ4 тіла 4 відносно осі Z
Враховуючи, що
Тепер диференціальне рівняння (2.7) набуває вигляду
Якщо до диференціальних рівнянь (2.1), (2.4), (2.8) додати кінематичні співвідношення
тоді отримаємо систему шести рівнянь в які входять невідомі: Розв’язуючи систему рівнянь (2.1), (2.4), (2.8), (2.9) маємо:
З урахуванням того, що m1=20кг, m2=2кг, m3=m4=3кг, r2=0,2м, R2=0,4м, і2=0,3м, R3=R4=0,3м, М=(16+11t2)
Для визначення закону руху тіла 1, інтегруємо двічи диференціальне рівняння (2.20), беручи до уваги початкові умови (2.2)
Перший інтеграл диференціального рівняння (2.20)
Закон руху тіла 1: ДС.3 Визначення реакцій в’язей тіла, що обертається навколо нерухомої осі Тонкий стержень вагою Р (рис. 3.1-3.5) жорстко скріплений з круговим диском (парні варіанти) або тонким кільцем (непарні варіанти) вагою Q та радіусом r. Система обертається навколо горизонтальної осі в вертикальній площині із стану спокою під дією моменту М. Знайти кутове прискорення, кутову швидкість та зусилля в опорах осі при повороті системи на кут Стержень, диск, кільце вважати однорідними тілами; тертям в підшипниках знехтувати. Дані для розрахунку приведені в таблиці 3.1.
Таблиця 3.1.
Приклад виконання завдання
Система тіл, що складається з стержня 1 вагою Р, однорідного диска 2 та кільця 3, що мають відповідно вагу Q2 та Q3 та радіус R, обертається навколо горизонтальної осі О (рис. 3.6.) під дією пари сил з моментом М. Знайти кутове прискорення, кутову швидкість та зусилля в опорах осі при повороті матеріальної системи на кут Прийняти: P=10H; Q2=20H; M=30Hм; Q3=10H; R=0,2м; AO=0,8м;
Рисунок 3.2
Рисунок 3.3
Рисунок 3.4
Рисунок 3.5
Рисунок 3.6 Розв’язання. На систему тіл діють активні сили Переміщенню тіл перешкоджає в’язь: циліндричний шарнір О, дію якого на тіло, на підставі аксіоми звільнення від в’язів, замінюємо реакціями в’язей
Для визначення сил М М де М=m1+m2+m3- маса системи тіл (m1= Fxе =Х0, Fyе=Y0-P-Q2-Q3. (3.2) Тепер із диференціальних рівнянь (3.1) отримаємо Х0=М Y0=M Щоб знайти реакції в’язей необхідно визначити прискорення центра мас
де
3.1.1 Визначення кутового прискорення Кутове прискорення тіл знайдемо на підставі диференціального рівняння обертального руху тіла навколо осі
де Iz – момент інерції системи тіл відносно осі Z, Момент інерції тіл IZ відносно осі дорівнює сумі моментів інерції тіл 1, 2, 3 відносно осі Z.
Момент інерції диска 2 відносно осі Z:
Момент інерції кільця 3 відносно осі Z:
Момент інерції стержня 1 відносно осі Z:
Тоді:
Момент зовнішніх сил матеріальної системи (рис.3.7) відносно осі Z
де OC Момент сили або момент пари сил беремо з додатним знаком, якщо він діє у напрямку обертання системи тіл. Диференціальне рівняння (3.5), враховуючи (3.6), запишеться:
Звідки:
При
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.228.171 (0.01 с.) |


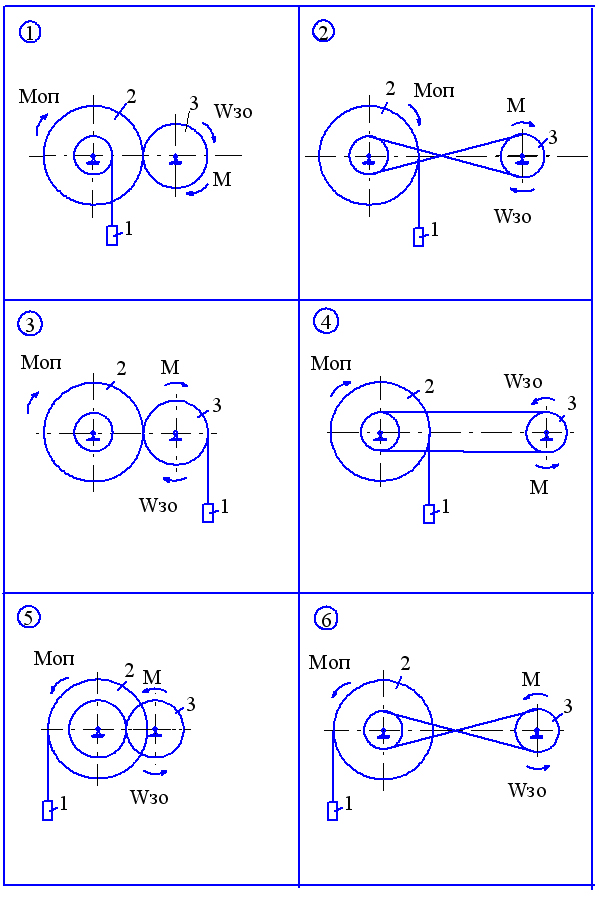
 Рисунок 2.2
Рисунок 2.2 Рисунок 2.3
Рисунок 2.3

 прикладеним до ступінчатого шківа 3 масою m3=3кг.
прикладеним до ступінчатого шківа 3 масою m3=3кг. =
=  . Більший радіус у шківа 2, R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2=0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3=R4=0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
. Більший радіус у шківа 2, R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2=0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3=R4=0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
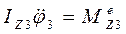
 - момент інерції тіла відносно осі z,
- момент інерції тіла відносно осі z,  - кутове прискорення тіла 3,
- кутове прискорення тіла 3,  - момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
- момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
 . (2.1)
. (2.1) ,
,  . (2.2)
. (2.2) та
та  , які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 2.7).
, які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 2.7). (2.3)
(2.3)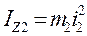 - момент інерції тіла 2 відносно осі Z.
- момент інерції тіла 2 відносно осі Z. , то рівняння (2.3) запишеться у вигляді
, то рівняння (2.3) запишеться у вигляді (2.4)
(2.4) , реакції циліндричного шарніра X4 та Y4.
, реакції циліндричного шарніра X4 та Y4.

 (2.7)
(2.7) - головний момент зовнішніх сил.
- головний момент зовнішніх сил.
 , а
, а  ,кінетичний момент системи LZ визначимо за формулою
,кінетичний момент системи LZ визначимо за формулою
 (2.8)
(2.8)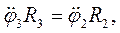

 (2.9)
(2.9)

 , M0=15
, M0=15  , отримаємо
, отримаємо . (2.20)
. (2.20)
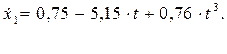

 .
. Рисунок 3.1
Рисунок 3.1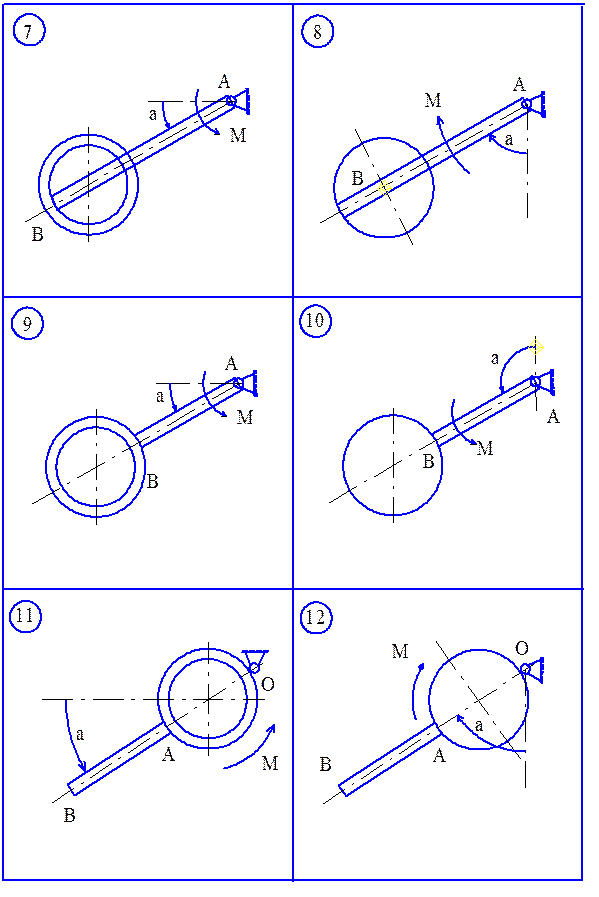




 ,
,  ,
,  та пара сил з моментом М (рис.3.7)
та пара сил з моментом М (рис.3.7) 0,
0,  0.
0.
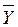 0 запишемо теорему про рух центра мас системи в проекціях на осі Х та Y.
0 запишемо теорему про рух центра мас системи в проекціях на осі Х та Y. с=Fxе, (3.1)
с=Fxе, (3.1) с=Fyе,
с=Fyе, , m2=
, m2=  , m3=
, m3=  ),
),  с,
с, +P (3.3)
+P (3.3) системи тіл
системи тіл (3.4)
(3.4) ,
,  ,
,  -кутова швидкість тіла,
-кутова швидкість тіла,  - кутове прискорення тіла (системи тіл.)
- кутове прискорення тіла (системи тіл.) .
. . (3.5)
. (3.5) - головний момент зовнішніх сил системи відносно осі Z.
- головний момент зовнішніх сил системи відносно осі Z. =
=  +
+  +
+ 


 .
. .
. .
. . (3.6)
. (3.6) , OC
, OC 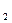 і OC
і OC  відстань осі обертання до центра мас відповідного тіла.
відстань осі обертання до центра мас відповідного тіла. .
. =
= 
 (3.7)
(3.7)



