
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В. О. Приятельчук, В. І. Риндюк, В. О. ФедотовСодержание книги
Поиск на нашем сайте
В. О. Приятельчук, В. І. Риндюк, В. О. Федотов
Теоретична механіка Динаміка матеріальної системи
Розрахунково-графічні та контрольні завдання
Міністерство освіти і науки України Вінницький національний технічний університет
В. О. Приятельчук, В. І. Риндюк, В. О. Федотов
Теоретична механіка Динаміка матеріальної системи
Розрахунково-графічні та контрольні завдання
Затверджено Вченою радою Вінницького національного технічного університету як навчальний посібник для студентів напрямів підготовки: 0921 - “Будівництво”; 0902 – “Інженерна механіка”; 0923 – “Зварювання”; 0922 – “Електромеханіка”; 0905 – “Енергетика”; 0906 – “Електротехніка”; 0907 – “Радіотехніка”. Протокол №2 від 30 вересня 2004р.
Вінниця ВНТУ 2005 УДК 531 (075) П 77
Рецензенти: В.Ф. Анісімов, доктор технічних наук, професор І.О. Сивак, доктор технічних наук, професор В.І. Савуляк, кандидат технічних наук, професор
Рекомендовано до видання Ученою радою Вінницького національного технічного університету Міністерства освіти і науки України
Приятельчук В.О., Риндюк В.І., Федотов В.О. П77 Теоретична механіка. Динаміка матеріальної системи. Розрахунково – графічні та контрольні завдання. Навчальний посібник. – Вінниця: ВНТУ, 2005. – 78с. В посібнику приведені сім завдань із розділу “Основні (загальні) теореми динаміки”. Кожне завдання має триста варіантів з прикладом виконання. Для студентів денної та заочної форми навчання. УДК 531(075)
©, В. Приятельчук, В. Риндюк, В. Федотов, 2005 Зміст 1. Порядок та основні вимоги до виконання роботи...........................4 2. Розрахунково-графічні та контрольні завдання...............................5 ДС.1 Використання теореми про рух центра мас для визначення переміщення тіл.........................................................................5 1.1 Приклад виконання завдання.....................................................11 ДС.2 Використання теореми про зміну кінетичного моменту для дослідження руху матеріальної системи...............................13 1.2 Приклад виконання завдання.....................................................19 ДС.3 Визначення реакцій в’язей тіла, що обертається навколо нерухомої осі............................................................................23 3.1 Приклад виконання завдання.....................................................23 3.1.1 Визначення кутового прискорення 3.1.2 Визначення кутової швидкості......................................31 3.1.3 Визначення реакції опор.................................................32 ДС.4 Використання теорем про рух центра мас та кінетичного моменту для дослідження руху матеріальної системи........33 4.1 Приклад виконання завдання.....................................................39 4.1.1 Визначення прискорення тіла 3.....................................39 4.1.2 Визначення реакції в’язей циліндричних шарнірів та зусиль між тілами.......................................................43 ДС.5 Визначення прискорення точок та кутових прискорень тіл за допомогою теореми про зміну кінетичної енергії системи.....................................................................................45 5.1 Приклад виконання завдання.....................................................45 ДС.6 Дослідження планетарного механізму з паралельними осями........................................................................................48 6.1 Приклад виконання завдання.....................................................48 ДС.7 Використання теореми про зміну кінетичної енергії для вивчення руху матеріальної системи...................................58 7.1 Приклад виконання завдання.....................................................64 ДС.8 Додаткові динамічні реакції в’язей твердого тіла, що обертається навколо нерухомої осі.......................................69 8.1 Приклад виконання завдання.....................................................69 Література...............................................................................................84
Розрахунково-графічні та контрольні завдання ДС.1 Використання теореми про рух центра мас для визначення переміщення тіл
Визначити переміщення призми 1 по горизонтальній гладенькій поверхні, якщо центр мас тіла 2 опустився на відстань S відносно призми 1 (вар. 1.1-1.19) або тіло 2 повернулося на заданий кут навколо горизонтальної осі (вар. 1.20-1.30). В початковий момент часу матеріальна система знаходиться у спокої. Дані для розрахунків приведені в табл. 1.1. (
Таблиця 1.1
Приклад виконання завдання По похилій площині (рис. 1.6) призми 1 маси m1=10кг спускається вантаж 2 (m2=6кг), який тягне за допомогою невагомої вантаж 3 масою m3=4кг. Знайти переміщення призми 1 по гладенькій горизонтальній площині, якщо тіло М2 опустилось по похилій площині на S=0,5м. Розв’язання. Покажемо зовнішні сили, які прикладені до матеріальної системи, що складається з призми 1 та тіл 2, 3. Такими самими є: P1=m1g – сила ваги призми, P2=m2g i P3=m3g – вага відповідно другого та третього вантажів, N – реакція гладенької горизонтальної поверхні.
Рисунок 1.6
Запишемо теорему про рух центра мас матеріальної системи в проекціях на вісь Х:
де Оскільки В початковий момент часу система знаходилась у спокої і тому
Таким чином, координата ХС центра мас матеріальної системи залишається сталою незалежно від переміщень тіл, що входять у систему. Визначимо положення центра мас системи в початковий момент часу:
Якщо вантаж 2 переміститься на величину
Враховуючи (1.2), із формули (1.3) отримаємо:
Переміщення
Тепер із формули (1.4) знаходимо переміщення призми.
Знак “мінус” вказує на те, що призма 1 перемістилася в сторону протилежну додатному напрямку осі Х.
Приклад виконання завдання
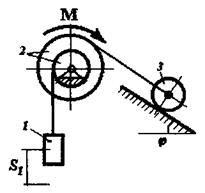
До вантажу 1 (рис. 2.6) масою m1=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом r2 (m2=2кг). Механічна система приводиться до руху моментом Знайти закон руху вантажу 1, якщо на тіло 2 діє момент опору МОП = 15 Н×м і при t=0 кутова швидкість тіла 3 -
Рисунок 2.6
Розв’язання. Розглянемо окремо рух тіл 2 і 3 та рух тіл 1 і 4. До тіла 3 (рис. 2.7) прикладені зовнішні сили: пара сил з моментом М, сила тяжіння P3=m3g, реакції циліндричного шарніра X3 і Y3, реакції тіла 2 – колове зусилля S3 і сила нормального тиску N3. Запишемо диференціальне рівняння обертання тіла 3 навколо нерухомої осі враховуючи, що якщо момент зовнішніх сил діє у напрямку руху тіла, тоді записуємо його з додатним знаком.
де
Рисунок 2.7
Початкові умови: при t=0, На тіло 2 діють такі зовнішні сили: сила тяжіння P2=m2g, реакції циліндричного шарніра X2 та Y2, натяг троса S2 (трос працює тільки на розтяг), реакції тіла 3 – Диференціальне рівняння обертання тіла 2 (рис. 2.8) навколо горизонтальної осі Z.
де Оскільки
До тіл 1 та 4 (рис. 2.9) прикладені зовнішні сили: сили тяжіння P1=m1g та P4=m4g, реакція троса
Рисунок 2.8
Теорема про зміну кінетичного моменту для тіл 1 та 4 (рис. 2.9) в проекціях на вісь Z запишеться:
Рисунок 2.9
де lZ – кінетичний момент системи тіл 1 та 4 відносно осі Z, Кінетичний момент LZ складається із моменту кількості руху LZ1 тіла 1 та кінетичного моменту LZ4 тіла 4 відносно осі Z
Враховуючи, що
Тепер диференціальне рівняння (2.7) набуває вигляду
Якщо до диференціальних рівнянь (2.1), (2.4), (2.8) додати кінематичні співвідношення
тоді отримаємо систему шести рівнянь в які входять невідомі: Розв’язуючи систему рівнянь (2.1), (2.4), (2.8), (2.9) маємо:
З урахуванням того, що m1=20кг, m2=2кг, m3=m4=3кг, r2=0,2м, R2=0,4м, і2=0,3м, R3=R4=0,3м, М=(16+11t2)
Для визначення закону руху тіла 1, інтегруємо двічи диференціальне рівняння (2.20), беручи до уваги початкові умови (2.2)
Перший інтеграл диференціального рівняння (2.20)
Закон руху тіла 1: Приклад виконання завдання
Система тіл, що складається з стержня 1 вагою Р, однорідного диска 2 та кільця 3, що мають відповідно вагу Q2 та Q3 та радіус R, обертається навколо горизонтальної осі О (рис. 3.6.) під дією пари сил з моментом М. Знайти кутове прискорення, кутову швидкість та зусилля в опорах осі при повороті матеріальної системи на кут Прийняти: P=10H; Q2=20H; M=30Hм; Q3=10H; R=0,2м; AO=0,8м;
Рисунок 3.2
Рисунок 3.3
Рисунок 3.4
Рисунок 3.5
Рисунок 3.6 Розв’язання. На систему тіл діють активні сили Переміщенню тіл перешкоджає в’язь: циліндричний шарнір О, дію якого на тіло, на підставі аксіоми звільнення від в’язів, замінюємо реакціями в’язей
Для визначення сил М М де М=m1+m2+m3- маса системи тіл (m1= Fxе =Х0, Fyе=Y0-P-Q2-Q3. (3.2) Тепер із диференціальних рівнянь (3.1) отримаємо Х0=М Y0=M Щоб знайти реакції в’язей необхідно визначити прискорення центра мас
де
3.1.1 Визначення кутового прискорення Кутове прискорення тіл знайдемо на підставі диференціального рівняння обертального руху тіла навколо осі
де Iz – момент інерції системи тіл відносно осі Z, Момент інерції тіл IZ відносно осі дорівнює сумі моментів інерції тіл 1, 2, 3 відносно осі Z.
Момент інерції диска 2 відносно осі Z:
Момент інерції кільця 3 відносно осі Z:
Момент інерції стержня 1 відносно осі Z:
Тоді:
Момент зовнішніх сил матеріальної системи (рис.3.7) відносно осі Z
де OC Момент сили або момент пари сил беремо з додатним знаком, якщо він діє у напрямку обертання системи тіл. Диференціальне рівняння (3.5), враховуючи (3.6), запишеться:
Звідки:
При
Визначення реакцій опори
Знайдемо координати центра мас системи тіл (рис.3.7)
Проекції прискорення центра мас (при Осі
Осі х та у:
Визначаємо проекції реакції в’язей циліндричного шарніра 0 (рис.3.6) на осі х та у (3.3). Х Y Реакція в’язі R шарніра 0. R=
Приклад виконання завдання Матеріальна система (рис. 4.6) починає рухатись із стану спокою під дією моменту М, що прикладається до тіла 1. Осі тіл 1 та 2 горизонтальні. Коефіцієнт тертя ковзання f. В точках контакту тіл ковзання відсутнє. Масою паса знехтувати. Тіло 1 – однорідний циліндр. Визначити прискорення тіла 3, натяг S5 у веденій 5 та ведучій 4 (S4) частині паса (прийняти S4=2S5), зусилля в точці контакту тіл 1 та 2, реакції в’язей циліндричних (нерухомих) шарнірів тіл 1, 2 та 3.
Прийняти: R1=0,25м; R2=0,45м; r2=0,15м; i2=0,4м; L=0,7м; m1=0,5кг; m2=5кг; m3=4кг; M=3t3 H M; t1=2c; f=0,4. Розв’язання. Розглянемо окремо рух кожного тіла матеріальної системи (рис. 4.6).
Рисунок 4.6
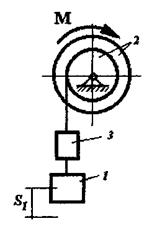
Приклад виконання завдання Матеріальна система (рис. 5.1) рухається під дією моменту М, що діє на тіло 1. Осі тіла 1 та 2 горизонтальні. В точках контакту тіл та паса ковзання відсутнє. Масою тіла знехтувати. Тіло 1 – однорідний циліндр. Визначити прискорення тіла 3 та кутові прискорення тіл 1 та 2 якщо: R1=0,25м; R2=0,45м; r2=0,15м; i2=0,4м; l=0,7м; m1=0,5кг; m2=5кг; m3=4кг; М=3t3Hм; t2=2c.
Розв’язання. Для дослідження руху матеріальної системи (рис. 5.1) використаємо теорему про зміну кінетичної енергії в диференціальній формі
де Т- кінетична енергія системи, Ne – потужність зовнішніх сил системи, Ni – потужність внутрішніх сил системи, Ni = 0 – тіла тверді, а пас абсолютно гнучкий та нерозтяжний. Кінетична енергія системи складається із кінетичної енергії тіл, що входять в систему Т=Т1+Т2+Т3. Тіла 1 та 2 обертаються навколо нерухомих горизонтальних осей і їх кінетична енергія знаходиться за формулами:
де Тіло 3 переміщується поступально із швидкістю V3, тоді
Взаємозв’язок між кінематичними характеристиками руху тіл (рис. 5.2)
Запишемо кінетичну енергію системи, враховуючи (5.2), (5.3) та (5.4), як функцію швидкості V3 тіла 3
Рисунок 5.2
Знайдемо потужність зовнішніх сил (рис. 5.2) матеріальної системи: сили тяжіння P1=m1g, P2=m2g, P3=m3g моменту М; реакції в’язей нерухомих (циліндричних) шарнірів X1 , Y1 , X2 , Y2 , NA , NB. Потужність сил X1 ,Y1 , P1 , X2 , Y2 , P2 , NA i NB дорівнює нулю тому, що точки прикладення сил не переміщуються. Тоді потужність Nе зовнішніх сил буде складатися із потужності моменту М та сили тяжіння тіла 3 - Р3.
де
Або
Теорема про зміну кінетичної енергії матеріальної системи (5.1) з врахуванням (5.5) та (5.6) запишеться:
Оскільки
Кутові прискорення тіл
Підставляючи дані умови задачі, отримаємо:
При t1=2c,
ДС.6 Дослідження планетарного механізму з паралельними осями
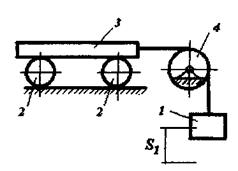
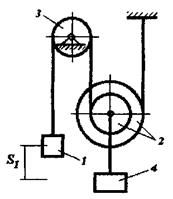
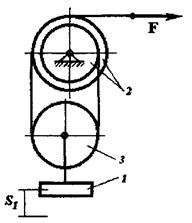
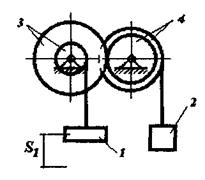
До вала I планетарного механізму (рис. 6.1 – 6.5), розташованого в горизонтальній площині (вал I вертикальний), прикладений обертальний момент М. Знайти кутову швидкість w вала I при t=t1. В початковий момент система знаходиться у спокої. Силами тертя знехтувати. Дані для розрахунків приведено в табл. 6.1. Вагою рухомих, нерухомих осей та водила знехтувати. Колеса з рухомими та нерухомими осями вважати однорідними круглими дисками. Радіус rз зубчастого колеса визначається із схеми механізму (рис. 6.1 – 6.5).
Таблиця 6.1
Приклад виконання завдання Вертикальний вал I (рис 6.6) із стану спокою приводиться до руху моментом М=(12-5w) Н·м. Знайти кутову швидкість вала I (водило) при t1=2c, якщо r1=0,4m; r2=0,2m; r4=1,0m. Зубчасті колеса з нерухомою віссю 1 та рухомою 2 і 3 – однорідні суцільні диски масами: m1=1кг, m2=2кг, m3=3кг. Силами тертя, масами рухомих осей та водила (вала I) знехтувати. Розв’язання. Планетарний механізм (рис 6.6) покажемо в площині його руху – горизонтальній (рис 6.7) Механізм рухається під дією зовнішніх сил: обертального моменту М; реакції циліндричного шарніра х1 та у1; реакції нерухомого колеса 4 – SA, NA, SB, NB; сили тяжіння P1, P2, P3 (направлені перпендикулярно до площини рис. 6.7). Для визначення кутової швидкості водила I застосуємо теорему про зміну кінетичної енергії матеріальної системи в диференціальному вигляді
Рисунок 6.1
Рисунок 6.2
Рисунок 6.3
Рисунок 6.4
Рисунок 6.6
де Т – кінетична енергія планетарного механізму, Ne та Ni потужність зовнішніх та внутрішніх сил системи. Оскільки в планетарному механізмі тіла тверді, то потужність внутрішніх сил дорівнює нулю (Ni=0). Кінетична енергія системи в даний момент часу складається з кінетичної енергії зубчастого колеса 1, кінетичних енергій рухомих зубчастих коліс (сателітів) 2 та 3.
Оскільки зубчасте колесо 1 обертається навколо нерухомої осі, то його кінетична енергія визначається за формулою
де Сателіти (рухомий блок зубчастих коліс 2 та 3) переміщується плоскопаралельно і їх кінетична енергія визначається таким чином:
Рисунок 6.7 де Vc – швидкість центра мас тіл 2 та 3, Знайдемо співвідношення між кутовими швидкостями тіл та швидкістю Vc, записавши їх через кутову швидкість водила I. Оскільки точка А (рис. 6.7) є миттєвим центром швидкостей сателітів 2 та 3, тоді очевидно що,
точка С також належить водилу I.
Тоді з (6.5), враховуючи (6.6).
Таким чином, кінетична енергія механічної системи (6.2), після підстановки в неї (6.3) і (6.4), та маючи на увазі (6.6) і (6.7), запишеться
Або
Потужність зовнішніх сил
На підставі теореми (6.1) і формул (6.8) та (6.9) отримаємо:
де Оскільки Початкові умови: При t=0, w=0. (6.12) В диференціальному рівнянні (6.11) розділимо змінні w та t.
Інтегруємо диференціальне рівняння (6.13) при початкових умовах (6.12).
Або
Виконуємо подальші перетворення:
Кутова швидкість водила I при t1=2c
де
Рисунок 7.1
Рисунок 7.2
Рисунок 7.3
Рисунок 7.4
Рисунок 7.5
Приклад виконання завдання
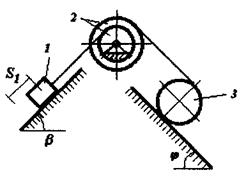
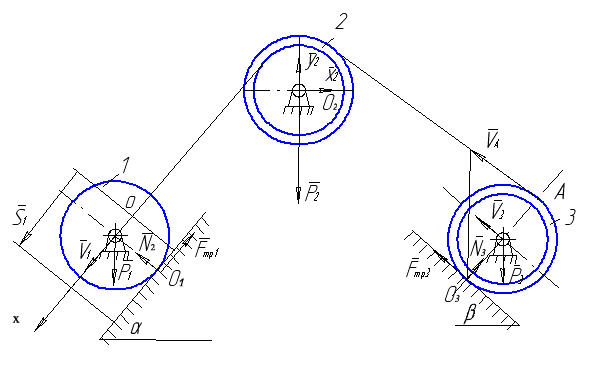
Визначити прискорення та швидкість центра мас тіла 1 у момент часу, коли він пройде шлях S1, якщо матеріальна система (рис.7.6) починає рухатися із стану спокою. Масами шнурів знехтувати. Тіла 1 та 3 рухаються без ковзання. Дано: m1=10кг; m2=2кг; m3=1кг; R2=0.4M; r2=0.3M; R3=0.3M; r3=0.2M; ρ2=0.35M; ρ3=0.25M; α=30˚; β=45˚; S1=0.4M
Рисунок 7.6
Розв’язання. Для дослідження руху матеріальної систем (рис.7.6) застосуємо теорему про зміну кінетичної енергії механічної системи в диференціальній формі.
де Т — кінетична енергія системи при 0<х≤S1; ∑Nі та ∑Nе− сума потужностей внутрішніх та зовнішніх сил системи. Матеріальна система (рис.7.6) складається із твердих тіл та нерозтяжних шнурів, тоді W
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.013 с.) |



 системи тіл.......30
системи тіл.......30 )
) ,
кг
,
кг
 ,
кг
,
кг
 град.
град.
 l,
м
l,
м
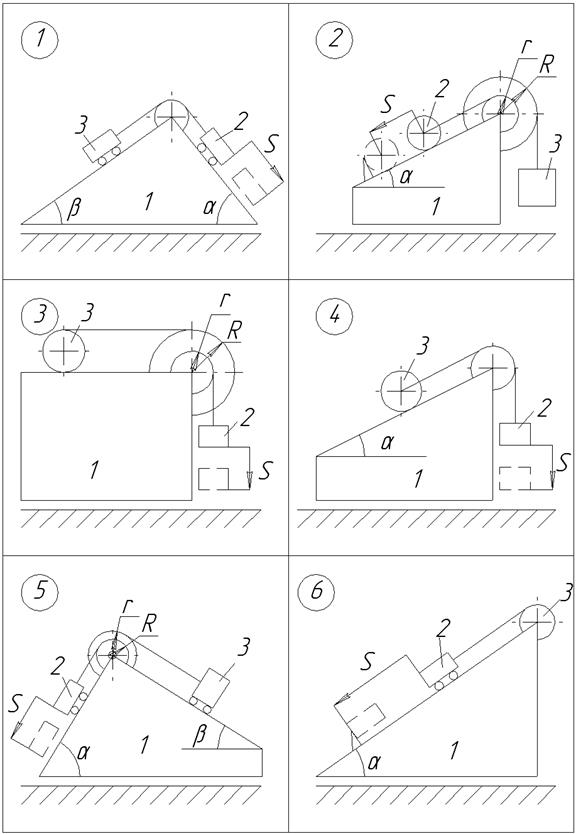 Рисунок 1.1
Рисунок 1.1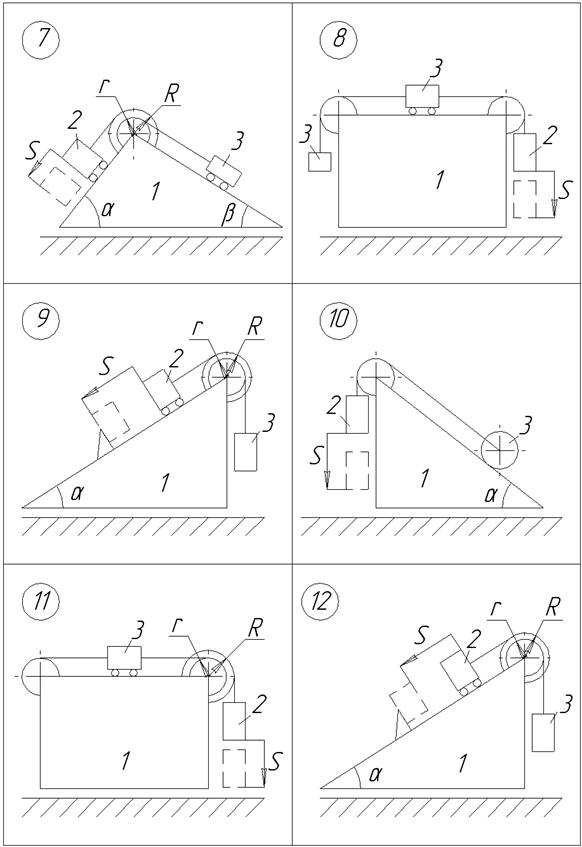 Рисунок 1.2
Рисунок 1.2 Рисунок 1.3
Рисунок 1.3 Рисунок 1.4
Рисунок 1.4 Рисунок 1.5
Рисунок 1.5
 (1.1)
(1.1) ,
, 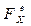 - проекція головного вектора зовнішніх сил на вісь Х.
- проекція головного вектора зовнішніх сил на вісь Х. = 0. Тоді
= 0. Тоді 
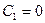 . Із формули (1.1) маємо:
. Із формули (1.1) маємо: .
.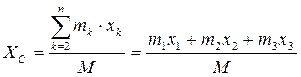 (1.2)
(1.2) , тоді тіло 3 – на
, тоді тіло 3 – на  , а призма 1 -
, а призма 1 -  і положення ХС центра мас знайдемо за формулою:
і положення ХС центра мас знайдемо за формулою: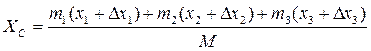 . (1.3)
. (1.3)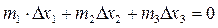 . (1.4)
. (1.4) та
та 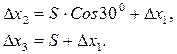

 прикладеним до ступінчатого шківа 3 масою m3=3кг.
прикладеним до ступінчатого шківа 3 масою m3=3кг. =
=  . Більший радіус у шківа 2, R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2=0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3=R4=0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
. Більший радіус у шківа 2, R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2=0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3=R4=0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
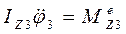
 - момент інерції тіла відносно осі z,
- момент інерції тіла відносно осі z,  - кутове прискорення тіла 3,
- кутове прискорення тіла 3,  - момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
- момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
 . (2.1)
. (2.1) ,
,  . (2.2)
. (2.2) та
та  , які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 2.7).
, які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 2.7). (2.3)
(2.3)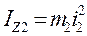 - момент інерції тіла 2 відносно осі Z.
- момент інерції тіла 2 відносно осі Z. , то рівняння (2.3) запишеться у вигляді
, то рівняння (2.3) запишеться у вигляді (2.4)
(2.4) , реакції циліндричного шарніра X4 та Y4.
, реакції циліндричного шарніра X4 та Y4.

 (2.7)
(2.7) - головний момент зовнішніх сил.
- головний момент зовнішніх сил.
 , а
, а  ,кінетичний момент системи LZ визначимо за формулою
,кінетичний момент системи LZ визначимо за формулою
 (2.8)
(2.8)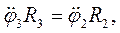

 (2.9)
(2.9)

 , M0=15
, M0=15  , отримаємо
, отримаємо . (2.20)
. (2.20)
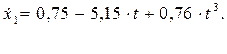

 Рисунок 3.1
Рисунок 3.1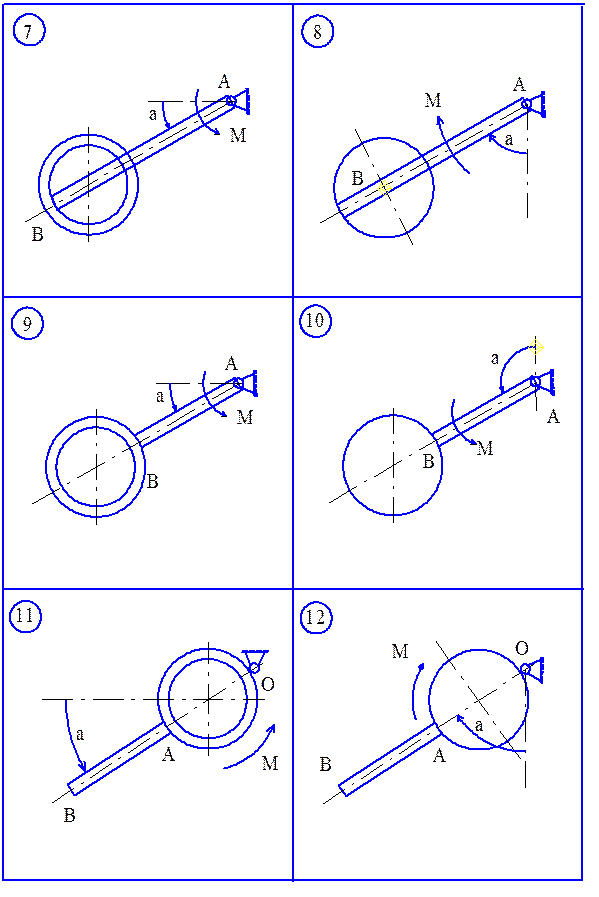




 ,
,  ,
,  та пара сил з моментом М (рис.3.7)
та пара сил з моментом М (рис.3.7) 0,
0,  0.
0.
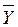 0 запишемо теорему про рух центра мас системи в проекціях на осі Х та Y.
0 запишемо теорему про рух центра мас системи в проекціях на осі Х та Y. с=Fxе, (3.1)
с=Fxе, (3.1) с=Fyе,
с=Fyе, , m2=
, m2=  , m3=
, m3=  ),
),  с,
с, +P (3.3)
+P (3.3) системи тіл
системи тіл (3.4)
(3.4) ,
,  ,
,  -кутова швидкість тіла,
-кутова швидкість тіла,  - кутове прискорення тіла (системи тіл.)
- кутове прискорення тіла (системи тіл.) .
. . (3.5)
. (3.5) - головний момент зовнішніх сил системи відносно осі Z.
- головний момент зовнішніх сил системи відносно осі Z. =
=  +
+  +
+ 


 .
. .
. .
. . (3.6)
. (3.6)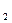 і OC
і OC  відстань осі обертання до центра мас відповідного тіла.
відстань осі обертання до центра мас відповідного тіла. .
. =
= 
 (3.7)
(3.7)

 ) на натуральні та декартові осі координат.
) на натуральні та декартові осі координат. та
та 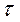 :
: 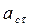 =
=  ,
,

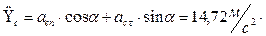
 н,
н, Н.
Н. Н.
Н.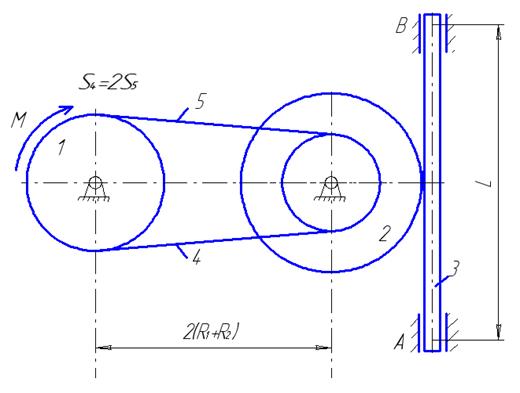
 Рисунок 5.1
Рисунок 5.1 , (5.1)
, (5.1) ,
,  , (5.2)
, (5.2) ,
,  - моменти інерції відповідно тіл 1 та 2, w1, w2 – кутові швидкості тіл.
- моменти інерції відповідно тіл 1 та 2, w1, w2 – кутові швидкості тіл. . (5.3)
. (5.3) ,
,  . (5.4)
. (5.4) . (5.5)
. (5.5)

 ,
, .
. . (5.6)
. (5.6)
 , тоді
, тоді . (5.7)
. (5.7) ,
,  .
.
 ,
, 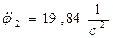 ,
,  .
.








 Рисунок 6.5
Рисунок 6.5
 (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3) - момент інерції колеса відносно головної центральної осі, що є віссю обертання тіла 1, w1 – кутова швидкість тіла 1.
- момент інерції колеса відносно головної центральної осі, що є віссю обертання тіла 1, w1 – кутова швидкість тіла 1. (6.4)
(6.4)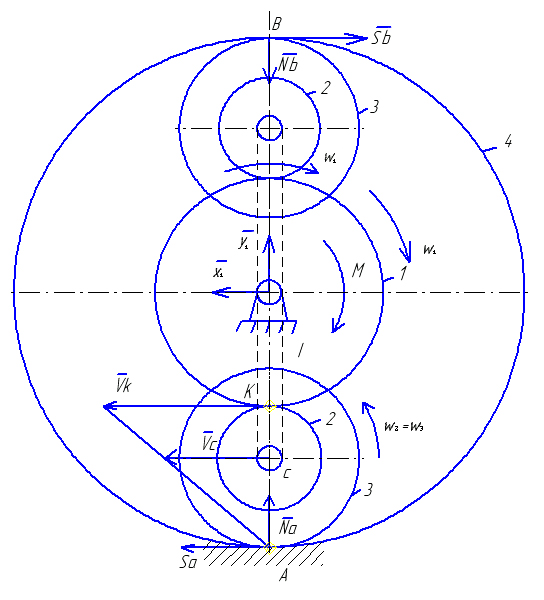
 та
та  - моменти інерції тіл 2 та 3 відносно головної центральної осі, w2=w3 – кутова швидкість сателітів (блока коліс 2 та 3).
- моменти інерції тіл 2 та 3 відносно головної центральної осі, w2=w3 – кутова швидкість сателітів (блока коліс 2 та 3). ,
,  ,
,  (6.5)
(6.5) (6.6)
(6.6) ,
,  (6.7)
(6.7)
 (6.8)
(6.8) (6.9)
(6.9)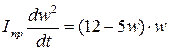 (6.10)
(6.10) M=(12-5 w) – обертальний момент, що діє на водило I.
M=(12-5 w) – обертальний момент, що діє на водило I. , тоді
, тоді  (6.11)
(6.11) (6.13)
(6.13)

 (6.14)
(6.14)
 ,
,  - радіус зубчастого колеса 3.
- радіус зубчастого колеса 3.







































 =∑Nе+∑Nі (7.1)
=∑Nе+∑Nі (7.1)


