
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дс. 5 визначення прискорення точок та кутових прискорень тіл за допомогою теореми про зміну кінетичної енергії системиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Матеріальна система (рис. 4.1-4.5) приводиться до руху моментом М. Знайти прискорення тіла 3 та кутові прискорення тіл в момент часу t=t1. Масами пасів та їх ковзанням по шківах знехтувати. В точках контакту тіл ковзання відсутнє. Однорідний диск 1 та ступінчатий шків 2 обертаються навколо горизонтальних осей. Дані для розрахунку приведені в таблиці 4.1 де m1, m2, m3 – маси тіл 1, 2 та 3; R1, R2, r2 – розміри тіл 1 та 2; і2 – радіус і перції тіла 2 відносно горизонтальної осі.
Приклад виконання завдання Матеріальна система (рис. 5.1) рухається під дією моменту М, що діє на тіло 1. Осі тіла 1 та 2 горизонтальні. В точках контакту тіл та паса ковзання відсутнє. Масою тіла знехтувати. Тіло 1 – однорідний циліндр. Визначити прискорення тіла 3 та кутові прискорення тіл 1 та 2 якщо: R1=0,25м; R2=0,45м; r2=0,15м; i2=0,4м; l=0,7м; m1=0,5кг; m2=5кг; m3=4кг; М=3t3Hм; t2=2c.
Розв’язання. Для дослідження руху матеріальної системи (рис. 5.1) використаємо теорему про зміну кінетичної енергії в диференціальній формі
де Т- кінетична енергія системи, Ne – потужність зовнішніх сил системи, Ni – потужність внутрішніх сил системи, Ni = 0 – тіла тверді, а пас абсолютно гнучкий та нерозтяжний. Кінетична енергія системи складається із кінетичної енергії тіл, що входять в систему Т=Т1+Т2+Т3. Тіла 1 та 2 обертаються навколо нерухомих горизонтальних осей і їх кінетична енергія знаходиться за формулами:
де Тіло 3 переміщується поступально із швидкістю V3, тоді
Взаємозв’язок між кінематичними характеристиками руху тіл (рис. 5.2)
Запишемо кінетичну енергію системи, враховуючи (5.2), (5.3) та (5.4), як функцію швидкості V3 тіла 3
Рисунок 5.2
Знайдемо потужність зовнішніх сил (рис. 5.2) матеріальної системи: сили тяжіння P1=m1g, P2=m2g, P3=m3g моменту М; реакції в’язей нерухомих (циліндричних) шарнірів X1 , Y1 , X2 , Y2 , NA , NB. Потужність сил X1 ,Y1 , P1 , X2 , Y2 , P2 , NA i NB дорівнює нулю тому, що точки прикладення сил не переміщуються. Тоді потужність Nе зовнішніх сил буде складатися із потужності моменту М та сили тяжіння тіла 3 - Р3.
де
Або
Теорема про зміну кінетичної енергії матеріальної системи (5.1) з врахуванням (5.5) та (5.6) запишеться:
Оскільки
Кутові прискорення тіл
Підставляючи дані умови задачі, отримаємо:
При t1=2c,
ДС.6 Дослідження планетарного механізму з паралельними осями
До вала I планетарного механізму (рис. 6.1 – 6.5), розташованого в горизонтальній площині (вал I вертикальний), прикладений обертальний момент М. Знайти кутову швидкість w вала I при t=t1. В початковий момент система знаходиться у спокої. Силами тертя знехтувати. Дані для розрахунків приведено в табл. 6.1. Вагою рухомих, нерухомих осей та водила знехтувати. Колеса з рухомими та нерухомими осями вважати однорідними круглими дисками. Радіус rз зубчастого колеса визначається із схеми механізму (рис. 6.1 – 6.5).
Таблиця 6.1
Приклад виконання завдання Вертикальний вал I (рис 6.6) із стану спокою приводиться до руху моментом М=(12-5w) Н·м. Знайти кутову швидкість вала I (водило) при t1=2c, якщо r1=0,4m; r2=0,2m; r4=1,0m. Зубчасті колеса з нерухомою віссю 1 та рухомою 2 і 3 – однорідні суцільні диски масами: m1=1кг, m2=2кг, m3=3кг. Силами тертя, масами рухомих осей та водила (вала I) знехтувати. Розв’язання. Планетарний механізм (рис 6.6) покажемо в площині його руху – горизонтальній (рис 6.7) Механізм рухається під дією зовнішніх сил: обертального моменту М; реакції циліндричного шарніра х1 та у1; реакції нерухомого колеса 4 – SA, NA, SB, NB; сили тяжіння P1, P2, P3 (направлені перпендикулярно до площини рис. 6.7). Для визначення кутової швидкості водила I застосуємо теорему про зміну кінетичної енергії матеріальної системи в диференціальному вигляді
Рисунок 6.1
Рисунок 6.2
Рисунок 6.3
Рисунок 6.4
Рисунок 6.6
де Т – кінетична енергія планетарного механізму, Ne та Ni потужність зовнішніх та внутрішніх сил системи. Оскільки в планетарному механізмі тіла тверді, то потужність внутрішніх сил дорівнює нулю (Ni=0). Кінетична енергія системи в даний момент часу складається з кінетичної енергії зубчастого колеса 1, кінетичних енергій рухомих зубчастих коліс (сателітів) 2 та 3.
Оскільки зубчасте колесо 1 обертається навколо нерухомої осі, то його кінетична енергія визначається за формулою
де Сателіти (рухомий блок зубчастих коліс 2 та 3) переміщується плоскопаралельно і їх кінетична енергія визначається таким чином:
Рисунок 6.7 де Vc – швидкість центра мас тіл 2 та 3, Знайдемо співвідношення між кутовими швидкостями тіл та швидкістю Vc, записавши їх через кутову швидкість водила I. Оскільки точка А (рис. 6.7) є миттєвим центром швидкостей сателітів 2 та 3, тоді очевидно що,
точка С також належить водилу I.
Тоді з (6.5), враховуючи (6.6).
Таким чином, кінетична енергія механічної системи (6.2), після підстановки в неї (6.3) і (6.4), та маючи на увазі (6.6) і (6.7), запишеться
Або
Потужність зовнішніх сил
На підставі теореми (6.1) і формул (6.8) та (6.9) отримаємо:
де Оскільки Початкові умови: При t=0, w=0. (6.12) В диференціальному рівнянні (6.11) розділимо змінні w та t.
Інтегруємо диференціальне рівняння (6.13) при початкових умовах (6.12).
Або
Виконуємо подальші перетворення:
Кутова швидкість водила I при t1=2c
де
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.01 с.) |

 Рисунок 5.1
Рисунок 5.1 , (5.1)
, (5.1) ,
,  , (5.2)
, (5.2) ,
,  - моменти інерції відповідно тіл 1 та 2, w1, w2 – кутові швидкості тіл.
- моменти інерції відповідно тіл 1 та 2, w1, w2 – кутові швидкості тіл. . (5.3)
. (5.3) ,
,  . (5.4)
. (5.4) . (5.5)
. (5.5)

 ,
, .
.
 . (5.6)
. (5.6)
 , тоді
, тоді . (5.7)
. (5.7) ,
,  .
.
 ,
, 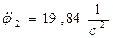 ,
,  .
.








 Рисунок 6.5
Рисунок 6.5
 (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3) - момент інерції колеса відносно головної центральної осі, що є віссю обертання тіла 1, w1 – кутова швидкість тіла 1.
- момент інерції колеса відносно головної центральної осі, що є віссю обертання тіла 1, w1 – кутова швидкість тіла 1. (6.4)
(6.4)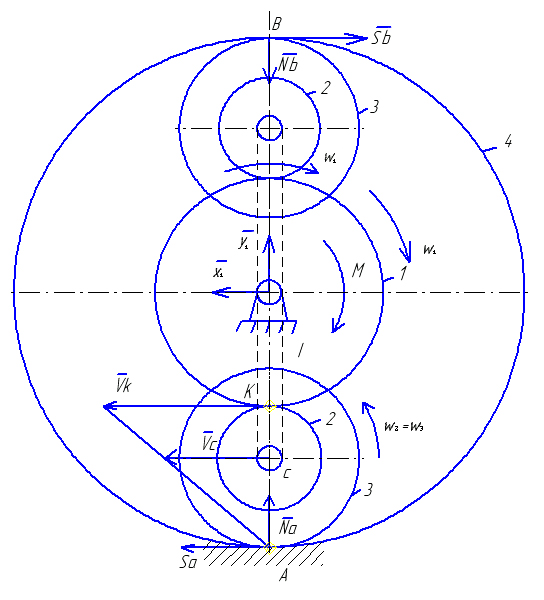
 та
та  - моменти інерції тіл 2 та 3 відносно головної центральної осі, w2=w3 – кутова швидкість сателітів (блока коліс 2 та 3).
- моменти інерції тіл 2 та 3 відносно головної центральної осі, w2=w3 – кутова швидкість сателітів (блока коліс 2 та 3). ,
,  ,
,  (6.5)
(6.5) (6.6)
(6.6) ,
,  (6.7)
(6.7)
 (6.8)
(6.8) (6.9)
(6.9)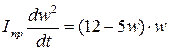 (6.10)
(6.10) M=(12-5 w) – обертальний момент, що діє на водило I.
M=(12-5 w) – обертальний момент, що діє на водило I. , тоді
, тоді  (6.11)
(6.11) (6.13)
(6.13)

 (6.14)
(6.14)
 ,
,  - радіус зубчастого колеса 3.
- радіус зубчастого колеса 3.


