
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення кутової швидкостіСодержание книги
Поиск на нашем сайте
Оскільки
При t=0; При t=t Інтегруємо рівняння (3.8)
Визначення реакцій опори
Знайдемо координати центра мас системи тіл (рис.3.7)
Проекції прискорення центра мас (при Осі
Осі х та у:
Визначаємо проекції реакції в’язей циліндричного шарніра 0 (рис.3.6) на осі х та у (3.3). Х Y Реакція в’язі R шарніра 0. R=
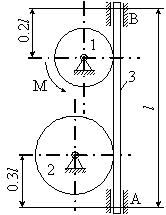
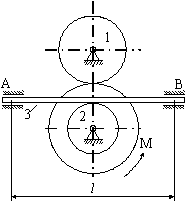
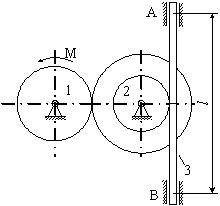
ДС. 4 Використання теорем про рух центра мас та кінетичного моменту для дослідження руху матеріальної системи Матеріальна система (рис 4.1-4.5) приводиться до руху моментом М. Знайти прискорення тіла 3, натяг пасів, зусилля між тілами, реакції в’язей в момент часу t=t1. Масами пасів та їх ковзанням по шківах знехтувати. Натяг у ведучій частині нескінченного паса (варіанти 2, 5, 6, 11, 14, 17, 23, 24, 28) вдвічі більший від натягу у веденій частині. Однорідний диск 1 та ступінчатий шків 2 обертаються навколо горизонтальних осей. В точках контакту тіл ковзання відсутнє. Коефіцієнт тертя ковзання f. Дані для розрахунків взяти з таблиці 4.1 де прийняті такі позначення: m1, m2, m3 – маси тіл 2 та 3; і2 – радіус інерції тіла 2 відносно горизонтальної осі, що проходить через центр мас тіла; R1, R2, r 2 – розміри тіл 1 та 2; l – відстань між опорами тіла 3. Таблиця 4.1
Рисунок 4.1
Рисунок 4.2
Рисунок 4.3
Рисунок 4.4
Рисунок 4.5
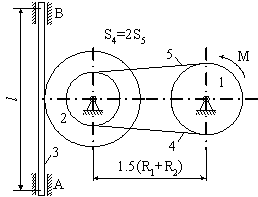
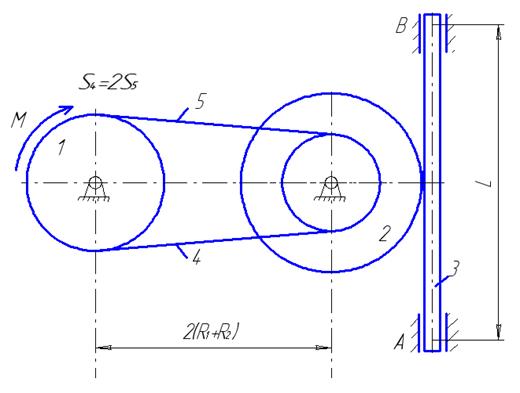
Приклад виконання завдання Матеріальна система (рис. 4.6) починає рухатись із стану спокою під дією моменту М, що прикладається до тіла 1. Осі тіл 1 та 2 горизонтальні. Коефіцієнт тертя ковзання f. В точках контакту тіл ковзання відсутнє. Масою паса знехтувати. Тіло 1 – однорідний циліндр. Визначити прискорення тіла 3, натяг S5 у веденій 5 та ведучій 4 (S4) частині паса (прийняти S4=2S5), зусилля в точці контакту тіл 1 та 2, реакції в’язей циліндричних (нерухомих) шарнірів тіл 1, 2 та 3.
Прийняти: R1=0,25м; R2=0,45м; r2=0,15м; i2=0,4м; L=0,7м; m1=0,5кг; m2=5кг; m3=4кг; M=3t3 H M; t1=2c; f=0,4. Розв’язання. Розглянемо окремо рух кожного тіла матеріальної системи (рис. 4.6).
Рисунок 4.6
Визначення прискорення тіла 3
Однорідне тіло 1 обертається навколо горизонтальної осі під дією моменту М (рис. 4.7) і до нього прикладені зовнішні сили: сила тяжіння P1=m1g; реакції циліндричного шарніра Х1 та Y1, зусилля у ланках паса S5 та S4.
Рисунок 4.7
Запишемо диференціальне рівняння обертання тіла 1 навколо нерухомої осі Z.
Необхідно врахувати, що момент сили або пари сил буде додатним, якщо він діє у напрямку руху тіла. Так, у рівнянні (4.1) момент сили S5 та пари сил з моментом М беремо із додатним знаком, а момент сили S4 – з від’ємним. Момент інерції тіла 1 відносно осі Z
На тіло 2 (рис 4.8) під час руху діють зовнішні сили: сила тяжіння P2=m2g, реакції нерухомого шарніра Х2 та Y2, зусилля у ланках паса У диференціальному рівнянні руху тіла 2 (рис. 4.8) навколо горизонтальної осі Z
сили
Для тіла 3 (рис. 4.9), що переміщується під дією сили тяжіння Р3=m3g, реакції нерухомих шарнірів NA та NB, реакції
Звичайно Якщо диференціальні рівняння (4.1), (4.3) і (4.5) розглянути з кінематичними співвідношеннями
Тоді отримаємо п’ять рівнянь з невідомими
Рисунок 4.9
Розв’язуючи систему рівнянь (4.1), (4.3), (4,5), (4,6), і, враховуючи (4.2) та (4.4), маємо
Або, підставляючи дані умови задачі, отримаємо
При t1=2c,
Визначення реакцій в’язей циліндричних шарнірів та зусиль між тілами
Для тіл 1 та 2 запишемо теорему про рух центра мас в проекціях на осі х та у. Тіло 1 (рис. 4.7)
Тіло 2 (рис 4.8)
Для тіла 3 (рис. 4.9) в проекціях на вісь Х:
В рівняннях (4.7) – (4.9) Отримали систему п’яти рівнянь
в якій сім невідомих величин: x1, y1, x2, y2, N2, NB, NA. Додаткові два рівняння отримаємо, використовуючи закон Амонтока-Кулона
та диференціальне рівняння обертального руху тіла 3 навколо осі Z що проходить через центр мас С (рис. 4.9) тіла 3
Тіло 3 рухається поступально і тому
Розв’язуючи систему рівнянь (4.6), (4.9) і (4.11), отримаємо
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.82 (0.009 с.) |

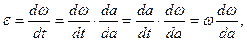 то вираз (3.7.) запишеться
то вираз (3.7.) запишеться =
=  (3.8)
(3.8)
 =0
=0 ;
;  =
= 




 ) на натуральні та декартові осі координат.
) на натуральні та декартові осі координат. та
та 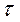 :
: 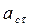 =
=  ,
,

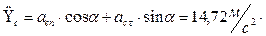
 н,
н, Н.
Н. Н.
Н.




 3
3

 4
4
 5
5

 6
6












































 . (4.1)
. (4.1) (4.2)
(4.2)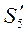
 та S4`, реакції тіла 1 – S2 та N2.
та S4`, реакції тіла 1 – S2 та N2.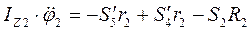 (4.3)
(4.3) та
та  , а момент інерції тіла 2 відносно осі Z знайдемо через радіус інерції і2
, а момент інерції тіла 2 відносно осі Z знайдемо через радіус інерції і2 (4.4)
(4.4) Рисунок 4.8
Рисунок 4.8 та
та  тіла 2, запишемо теорему про рух центра мас в проекціях на вісь Y (вісь Y направляється в сторону руху тіла 3)
тіла 2, запишемо теорему про рух центра мас в проекціях на вісь Y (вісь Y направляється в сторону руху тіла 3) (4.5)
(4.5)
 ,
,  . (4.6)
. (4.6)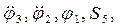





 (4.7)
(4.7) (4.8)
(4.8)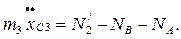 (4.9)
(4.9) оскільки центри мас тіл 1, 2 знаходяться на нерухомих осях обертання тіл, а координати XC3 тіла 3 є сталою величиною.
оскільки центри мас тіл 1, 2 знаходяться на нерухомих осях обертання тіл, а координати XC3 тіла 3 є сталою величиною. (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)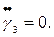 Таким чином, із (4.10) маємо
Таким чином, із (4.10) маємо (4.11)
(4.11)



