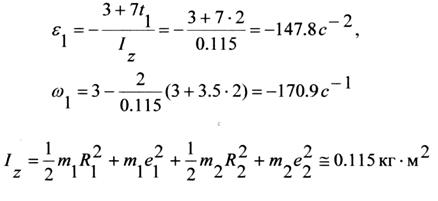Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ДC.7 Використання теореми про зміну кінетичної енергії для вивчення руху матеріальної системиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
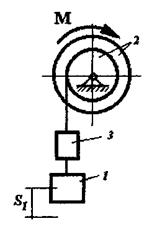
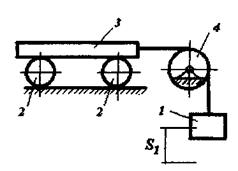
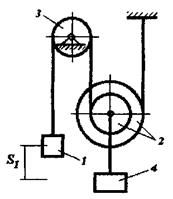
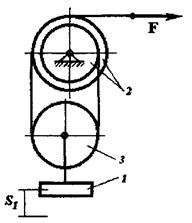
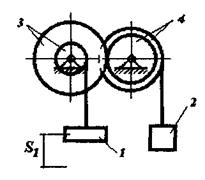
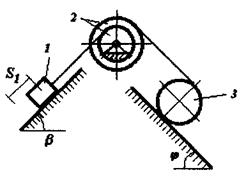
Матеріальна система(рис.7.1-7.5) рухається із стану спокою під дією сили тяжіння. Знайти прискорення та швидкість тіла 1 у момент часу, коли воно пройде шлях S. Масами шнурів, силами опору в шарнірах знехтувати. Тіла котяться по поверхнях без ковзання. Величини для розрахунків наведені в табл. 7.1 де прийнято такі позначення: m1,m2,m3 – маси тіл 1, 2, 3; R2, r2, R3, r3 — найбільші та найменші розміри ступінчастих шківів тіл 2 та 3; ρ2x, ρ3x — радіуси інерції ступінчастих шківів 2 та 3 відносно осі обертання; α,β кути нахилу площин до горизонту. Якщо тіла (шківи) 2 або 3 однорідні, тоді при розрахунках брати R2, R3. Шнури над похилими площинами паралельні цим площинам.
Таблиця 7.1
Рисунок 7.1
Рисунок 7.2
Рисунок 7.3
Рисунок 7.4
Рисунок 7.5
Приклад виконання завдання
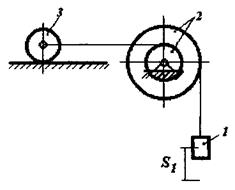
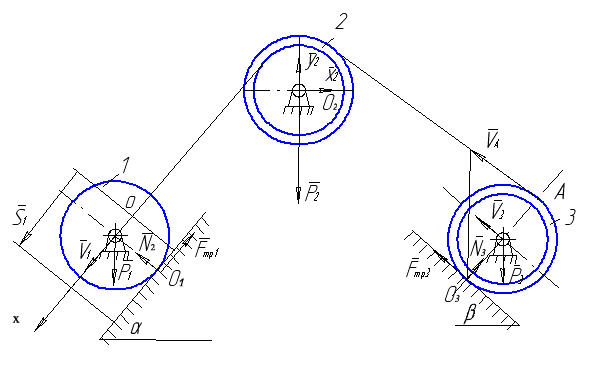
Визначити прискорення та швидкість центра мас тіла 1 у момент часу, коли він пройде шлях S1, якщо матеріальна система (рис.7.6) починає рухатися із стану спокою. Масами шнурів знехтувати. Тіла 1 та 3 рухаються без ковзання. Дано: m1=10кг; m2=2кг; m3=1кг; R2=0.4M; r2=0.3M; R3=0.3M; r3=0.2M; ρ2=0.35M; ρ3=0.25M; α=30˚; β=45˚; S1=0.4M
Рисунок 7.6
Розв’язання. Для дослідження руху матеріальної систем (рис.7.6) застосуємо теорему про зміну кінетичної енергії механічної системи в диференціальній формі.
де Т — кінетична енергія системи при 0<х≤S1; ∑Nі та ∑Nе− сума потужностей внутрішніх та зовнішніх сил системи. Матеріальна система (рис.7.6) складається із твердих тіл та нерозтяжних шнурів, тоді ∑ Nі=0. (7.2)
І диференціальне рівняння (6.1) набуває вигляду
Знайдемо кінематичні співвідношення між швидкостями точок, кутовими швидкостями тіл записавши їх через швидкість V1 центра мас тіла1. Кутова швидкість тіла 1, враховуючи, що миттєвий центр швидкості тіла 1 знаходиться в точці О1 (рис.7.6) w 1 = де R1 – радіус однорідного суцільного диска (тіла) 1. Кутова швидкість тіла 2
Швидкість точки А, враховуючи, що тіла 2 та 3 з’єднані нерозтяжним шнуром.
Оскільки точка О3 – миттєвий центр швидкості тіла 3, тоді
Із (7.6) та (7.7) визначаємо кутову швидкість тіла 3
Швидкість V3 центра мас тіла 3
Знайдемо переміщення центра мас тіла 3. Оскільки
i, враховуючи (7.9), отримаємо
або
При t = 0, S1 = 0, та S3 = 0 і після інтегрування (7.11) маємо
Знайдемо кінетичну енергію матеріальної системи як суму кінетичних енергій тіл 1,2 та 3. Т=Т1+Т2+Т3 (7.13) Кінетична енергія тіла 1, що рухається плоскопаралельно,
де
Тіло 2 обертається навколо горизонтальної осі і кінетична енергія знаходиться за формулою
де І2 =
Кінетична енергія тіла 3
де І3 =
Тепер кінетичну енергію (7.13) системи, враховуючи (7.14) – (7.16), визначимо за формулою
Потужність зовнішніх сил під дією яких рухається матеріальна система (рис. 7.6)
де Тоді, враховуючи що (7.9)
отримаємо
Підставляючи (7.17) і (7.18) в (7.3), маємо
Оскільки
Або, підставляючи дані умови задачі,
Знайдемо швидкість центра мас тіла 1. Рівняння (7.19) запишемо у вигляді:
При t=0, V10=0, S10=0. При t=t, V1t=V1, S1t=S1 (7.21) де t - час, за який центр мас тіла 1 пройде шлях S1. Інтегруючи рівняння (7.20) за умовами (7.21), визначаємо швидкість центра мас тіла 1 за час t.
або підставляючи числові дані, отримаємо:
ДС.8 Додаткові динамічні реакції в'язей твердого тіла, що обертається навколо нерухомої осі
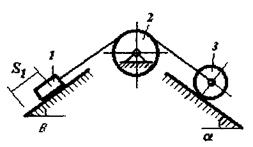
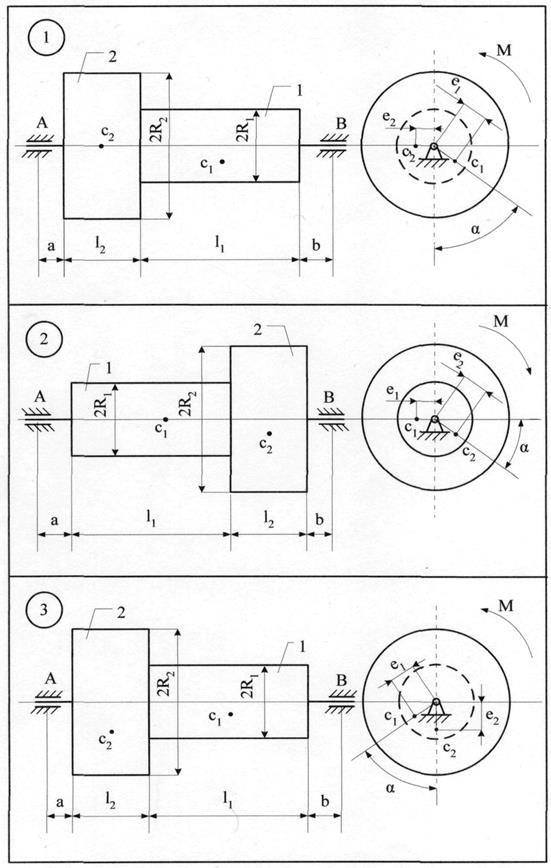
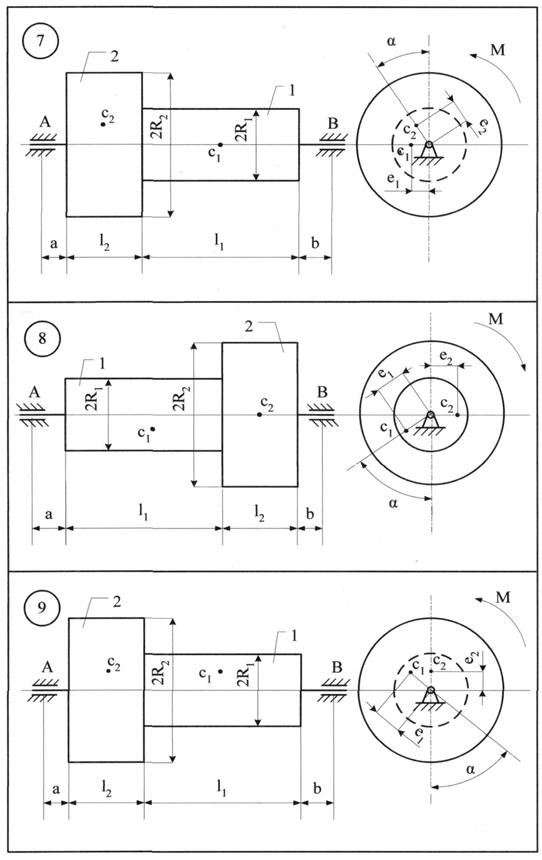
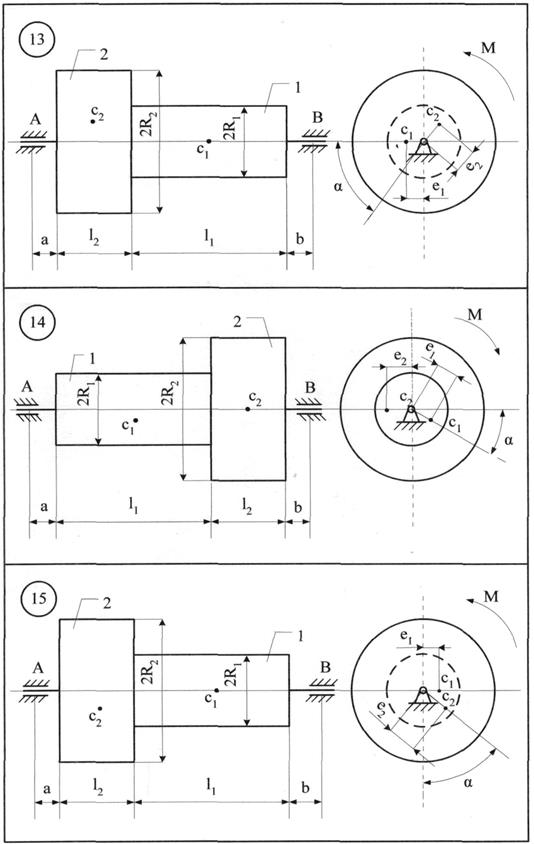
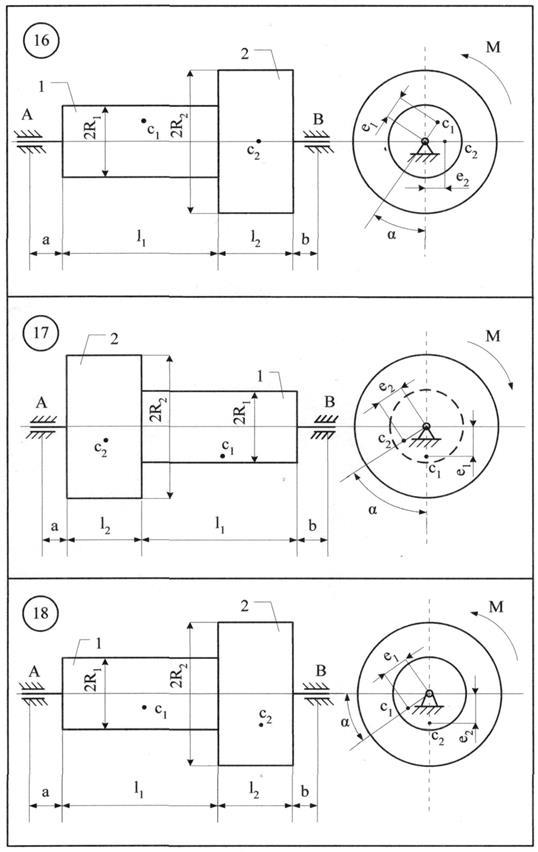
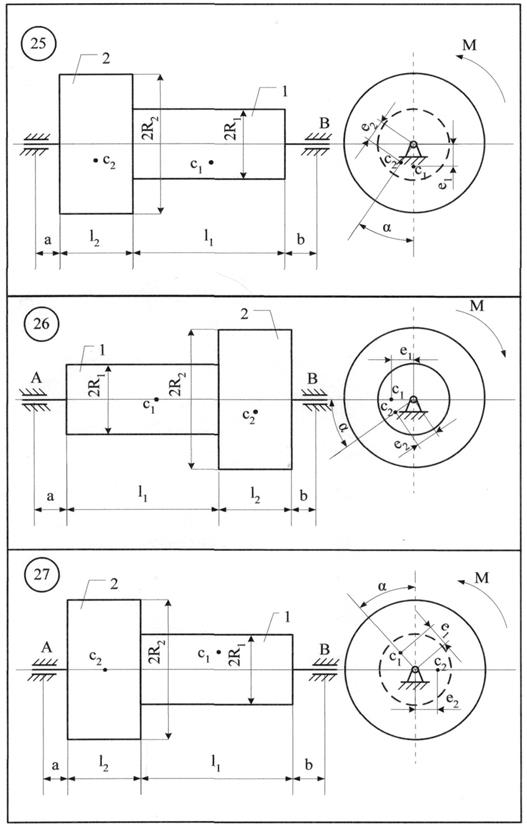
Однорідні тіла 1 та 2 (рис. 8.1 - 8.10) обертаються навколо нерухомої осі z під дією моменту М. Центри мас тіл зміщені від осі обертання (статична неврівноваженість тіл) на величини е1 та е2, відповідно. Знайти додаткові динамічні реакції циліндричних шарнірів А і В при t = t1, і порівняти їх зі статичними, якщо при t = 0 кутова швидкість тіл Дані для розрахунку приведені в табл. 8.1. Якщо Таблиця 8.1
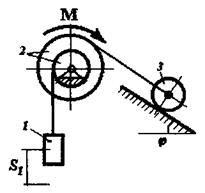
Приклад виконання завдання До системи однорідних тіл 1 та 2 (рис. 8.11), що обертаються з кутовою швидкістю
m1=3 кг; m2=5 кг; е1=0,1 мм;е2= 0,3 мм; l1= 0,25 м; l2 = 0,25 м; а = 0,05 м; b = 0,15 м; R1=0,1 м; R2=0,2 м.
Розв'язання. Переміщенню тіл 1 та 2 (рис 8.11) перешкоджають в'язі: нерухомі (циліндричні) шарніри А і В. На підставі аксіоми звільнення від
Рисунок 8.1
Рисунок 8.2
Рисунок 8.3
Рисунок 8.4
Рисунок 8.5
Рисунок 8.6
Рисунок 8.7
Рисунок 8.8
Рисунок 8.9
Рисунок 8.10 в'язей, дію шарнірів А і В та тіла замінюємо реакціями в'язей – YA, XA, YB, Рисунок 8.11 Реакції YA, XA, YB, XB запишемо як суму статичних YAC, XAC, YBC, XBC та додаткових динамічних реакцій YAД, XAД, YBД, XBД. YA = YAC + YAД, XA = XAC + XAД, (8.1) YB = YBC + YBД, XB = XBC + XBД.
Статичні реакції в'язей визначаються при
Розв'язуючи систему рівнянь, маємо:
таким чином маємо: RAC = 54,85 Н, RBC = 23,63 Н.
де Ixzi і Iуzi - доцентрові моменти інерції тіл (i = 1,2). Кутову швидкість
де IZ - момент інерції тіл відносно осі z. Оскільки
Інтегруємо диференціальне рівняння (8.4) при початкових умовах: при t1= 0,
Звідки: Визначимо кутове прискорення t1 = 2 c.
де
Оскільки значення Координати центра мас та доцентрові моменти Ixzi і Iуzi тіл 1 і 2 (рис. 8.11):
Або, підставляючи числові дані, отримаємо:
Тепер із рівнянь (8.2) знаходимо додаткові динамічні реакції шарнірів А і В через їх проекції на осі X та У.
Додаткові динамічні реакції циліндричних шарнірів А і В
При t1= 2 с додаткові динамічні реакції шарнірів складають 62,2% для шарніра А та 29,2% для шарніра В від статичних реакцій в'язей.
Література 1. Айзенберг Т.Б., Воронов Н.М., Осецкий В.М. Руководство к решению задач по теоретической механике.-М.:Высш.шк., 1968. – 436 с. 2. Бать М.Н., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: В 3 т.-Т.2.: Наука, 1985. – 560 с. 3. Березова О.В., Друшляк Г.Е., Солодовников Р.В. Теоретическая механика: Сб. задач. – К.: Висш. шк. Головное изд-во, 1980. –324 с. 4. Бражниченко Н.А. и др. Сборник задач по теоретической механике / Н.А. Бражниченко, Н.Л. Кац, Б.Л. Минцберг, В.Н. Морозов. –М.: Судпромгиз, 1963. – 562 с. 5. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: В 2 т. – Т.2. – М.: Наука, 1979. –461 с. 6. Бухгольц Н.Н. Основной курс теоретической механики: В 2 ч. – М.: Наука, 1967. – ч.1. – 468 с.; ч.2. – 332 с. 7. Гернет М.М. Курс теоретической механики. – М.: Высш. шк., 1981. – 303 с. 8. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.: Высш. шк., 1974. – 528 с. 9. Кильчевский Н.А. Курс теоретической механики: В 2т. –М.: Наука, 1972 – 1977. – Т.1. – 456 с.; Т.2. – 462 с. 10. Лойценский Л.Г., Лурье А.И. Курс теоретической механики: В 2 т. –М.: Наука, 1984. – Т.1. – 352 с.; Т.2. – 640 с. 11. Павловский М.А. Теоретична механіка: Підручник. – К.: Техніка, 2002. –512 с. 12. Савин Г.Н., Путята Т.В., Фрадлин Б.Н. Курс теоретической механики. –К.: Высш. шк., 1973. – 359 с. 13. Сборник заданий для курсових работ по теоретической механике: Учеб. пособ. для техн. вузов/ Яблонский А.А., Норейко С.С., Вольфсон С.А. и др.; Под ред. А.А. Яблонского. – 4-е изд., пере раб. и доп. – М.: Высш. шк., 1985. – 367 с. 14. Тарг С.М. Кратний курс теоретической механіки. – М.: Наука, 1974. – 400 с. 15. Технічна механіка. Кн..1. Теоретична механіка: Підручник/ Д.В. Чернілевський, Я.Т. Кіницький, В.М. Колосов та ін. За ред. Д.В. Чернілевського. –К.: НМК ВО, 1992. – 384 с. 16. Яблонський А.А., Никифорова В.М. Курс теоретической механики: В 2т. – М.: Высш. шк., 1977. – Т.1. – 431 с.; Т.2. – 532 с. 17. Яскілка М.Б. Збірник завдань для розрахунково-графічних робіт з теоретичної механіки: Посібник. – К.: Вища. шк.: Веселка, 1999. – 351с.
Навчальне видання
Володимир Олексійович Приятельчук Володимир Іванович Риндюк Валерій Олександрович Федотов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.01 с.) |




 3
3

 4
4
 5
5

 6
6









































 =∑Nе+∑Nі (7.1)
=∑Nе+∑Nі (7.1) (7.4)
(7.4)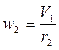 (7.5)
(7.5)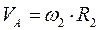 . (7.6)
. (7.6) (7.7)
(7.7) . (7.8)
. (7.8) . (7.9)
. (7.9)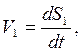
 (7.10)
(7.10)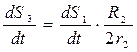
 . (7.11)
. (7.11) . (7.12)
. (7.12)
 − момент інерції тіла 1 відносно центральної осі. Тоді, враховуючи (7.4),
− момент інерції тіла 1 відносно центральної осі. Тоді, враховуючи (7.4),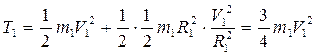 . (7.14)
. (7.14)
 − момент інерції тіла 3 відносно головної центральної осі, w 2 − кутова швидкість тіла 2 (7.5). Тоді
− момент інерції тіла 3 відносно головної центральної осі, w 2 − кутова швидкість тіла 2 (7.5). Тоді . (7.15)
. (7.15)
 − момент інерції тіла 3 відносно головної центральної осі,
− момент інерції тіла 3 відносно головної центральної осі, 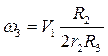 - (7.8),
- (7.8),  − швидкість центра мас тіла 3.
− швидкість центра мас тіла 3. . (7.16)
. (7.16) . (7.17)
. (7.17) ,
,



 (7.18)
(7.18)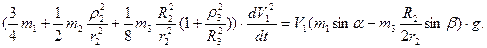 (7.19)
(7.19) (а1 – прискорення центра мас тіла 1), тоді
(а1 – прискорення центра мас тіла 1), тоді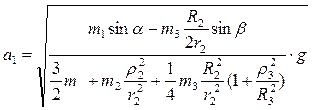

 (7.20)
(7.20)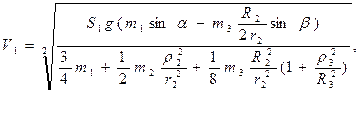

 .
. , град
, град
 , c-1
, c-1





 XB (рис. 8.12).
XB (рис. 8.12). Рисунок 8.12
Рисунок 8.12 = 0,
= 0,  = 0 з рівнянь (рис.8.12):
= 0 з рівнянь (рис.8.12):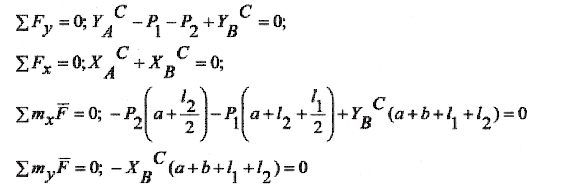


 Запишемо рівняння для визначення додаткових динамічних реакцій в'язей:
Запишемо рівняння для визначення додаткових динамічних реакцій в'язей: - кутове прискорення і
- кутове прискорення і  - кутова швидкість тіл при t1 = 2 с,
- кутова швидкість тіл при t1 = 2 с,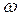 та кутове прискорення
та кутове прискорення  тіл знайдемо із диференціального рівняння руху тіл навколо осі z
тіл знайдемо із диференціального рівняння руху тіл навколо осі z (8.3)
(8.3)
 , тоді
, тоді (8.4)
(8.4)
 (8.5)
(8.5)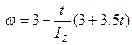
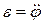 (8.3) та кутову швидкість (8.5) при
(8.3) та кутову швидкість (8.5) при