Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И диаграмма распределения ее мдсСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Примем, что вся указанная МДС расходуется на преодоление магнитного сопротивления воздушных зазоров, т. е. что магнитное сопротивление ферромагнитных участков магнитной цепи машины равно нулю. При этом распределение МДС вдоль окружности статора имеет прямоугольную форму. Во всех точках воздушного зазора действует неизменная МДС: F = 0,5F к; при переходе через середину пазов знак ее изменяется в соответствии с изменением полярности статора на данном участке. Прямоугольное распределение МДС можно разложить в ряд Фурье и представить в виде суммы синусоид. При этом для момента времени, соответствующего максимальному току в катушке, имеем Fx = ( + (1/5)cos5πx/τ +... + (1/n)cosnπx/τ], (1.3) где х — расстояние от оси симметрии обмотки, называемой осью фазы. Следовательно, при максимальном значении тока амплитуда первой гармонической МДС для сосредоточенной обмотки Fx = (2 Разложение в ряд Фурье позволяет количественно оценить отклонение кривой МДС от синусоидальной формы. При сосредоточенной обмотке это отклонение очень велико, поэтому такая обмотка получила ограниченное применение. МДС распределенной обмотки. Для улучшения формы кривой распределения поля обмотку каждой фазы размещают в нескольких пазах. Это улучшает и условия охлаждения обмотки. На рис. 1.9, а показана двухполюсная машина с обмоткой фазы, расположенной в шести пазах (при q = 3). МДС распределенной обмотки можно определить как сумму МДС трех сосредоточенных катушек с числом витков в каждой w′ = w /3, сдвинутых в пространстве на угол α = πb / τ, где b — расстояние между осями соседних пазов. Форма распределения результирующей МДС получается в этом случае ступенчатой (рис. 1.9, б). При максимальном значении тока в фазе катушки, расположенные в пазах 2 — 2', 3 — 3' и 1—1', создают в воздушном зазоре следующие значения МДС: Fn2x = (0,9Iw/3)[cos(πx/τ) + (1/3)cos(3πx/τ) + (1/5)cos(5πx/τ) +...]; Fn3x = (0,9Iw/3){cos[π(x-b)/τ] + (1/3)cos[3π(x-b)/τ] + + (1/5)cos[5π(x-b)/τ] +...}; Fn1x = (0,9Iw/3){cos[π(x+b)/τ] + (1/3)cos[3π(x+b)/τ] + + (1/5)cos[5π(x+b)/τ] +...}. Аналитическое выражение для результирующего распределения МДС обмотки можно получить, суммируя МДС каждой из катушек. Наиболее удобно это сделать, изобразив векторами пространственные гармонические МДС. Амплитудные значения первой, третьей и других гармонических результирующей МДС можно определить путем векторного сложения амплитуд соответствующих гармонических МДС
Рис. 1.9 - Схема двухполюсной машины с распределенной обмоткой И диаграмма распределения ее МДС
Рис. 1.10 - Диаграмма сложения векторов МДС катушек статора При распределенной обмотке Амплитудное значение первой гармонической результирующей МДС F 1= 2R sin (q α / 2 ), где R — радиус окружности, описанной вокруг векторов Таким образом (см. рис. 1.10, а) F1 = (0,9Iw/3)sin(qα/2)sin(α/2), (1.5) или в более общем виде (заменяя число «три» в знаменателе значением q) F1 = 0,9Iw sin(qα/2)[qsin(α/2)]. (1.5,a) Сравнивая (1.5а) и (1.4), можно установить, что амплитуда первой гармонической результирующей МДС при распределенной обмотке отличается от соответствующего значения при сосредоточенной обмотке только множителем kp1 =sin(qα/2)[qsin(α/2)], (1.6) называемым коэффициентом распределения обмотки для первой гармонической. Этот коэффициент равен отношению векторной суммы МДС, создаваемых катушками, расположенными во всех пазах данной фазы, к их алгебраической сумме. При векторном сложении амплитудных значений третьих гармонических МДС катушек ν-й гармонической коэффициент распределения обмотки kpν =sin(qνα/2)[qsin(να/2)], (1.7) где να — угол сдвига между ν-ми гармоническими МДС отдельных катушек. МДС при укорочении шага обмотки. Из приведенных данных следует, что при распределении обмотки происходит сильное ослабление ряда высших гармонических (пятой, седьмой). Но некоторые гармонические ослабляются незначительно. Поэтому часто наряду с распределением применяют укорочение шага обмотки, т. е. расстояние у между сторонами каждой катушки берут меньшим полюсного деления τ. В этом случае обмотку выполняют двухслойной, причем одна сторона каждой катушки находится в нижнем слое, а другая — в верхнем. В качестве примера на рис. 1.11, а показано расположение двухслойной обмотки в пазах двухполюсной машины при q = 3. Обмотка каждой фазы состоит из шести катушек. Стороны первой, второй и третьей катушек лежат в нижних слоях пазов 1, 2 и 3 и в верхних слоях пазов 2', 3' и 4'. Стороны четвертой, пятой и шестой катушек — в верхних слоях 2, 3 и 4 и в нижних слоях пазов 1′, 2' и 3'. Распределение МДС вдоль окружности статора для этой обмотки приведено на рис. 1.11, б.
Рис. 1.11 - Схема двухполюсной машины с двухслойной обмоткой с укороченным шагом и диаграмма распределения ее МДС МДС F xраспределенной обмотки с укороченным шагом можно определить как сумму МДС F' xи F' xдвух распределенных обмоток с диаметральным шагом и числом витков w ' = w /2, сдвинутых относительно друг друга на угол β = π (τ y)/τ. Одна из этих обмоток состоит из трех катушек, расположенных в нижних слоях пазов: 1 — 1′, 2 — 2', 3 — 3'; вторая обмотка — из трех катушек, расположенных в верхних слоях пазов: 2—2', 3 — 3' и 4 — 4'. Амплитуда первой гармонической результирующей МДС F1 находится путем векторного сложения амплитуд первых гармонических МДС F1 = 2F′1 cos(β/2)=0,9Iwkp1ky1,(1.8) где ky1 = cos(β/2) (1.9) — коэффициент укорочения. Для высших гармонических сдвиг по фазе между МДС указанных двух обмоток равен νβ. При этом коэффициент укорочения kyν = cos(νβ/2). (1.9,а) Поскольку для высших гармонических ν> 1, для некоторых из них k у<< 1. Следовательно, укорочение шага обмоток улучшает форму распределения кривой МДС. Выбирая соответствующее укорочение шага обмотки, можно полностью уничтожить одну из высших гармонических, для которой νβ = π. МДС при скосе пазов. В некоторых машинах применяют скос пазов на роторе или статоре на некоторый угол γ. В связи с этим МДС по образующей цилиндра статора постепенно изменяется: если у одного края статора образующая совпадает с осью паза, то затем она постепенно все больше отклоняется от оси этого паза. Скос пазов эквивалентен равномерному распределению обмотки по дуге, соответствующей углу γ. Поэтому, полагая в q α. = γи q sin (α/2) = γ/2, получаем коэффициент скоса пазов для первой и высших гармонических МДС kc1 =(sinγ/2)/(γ/2) и kcν = (sinνγ/2)/(νγ/2). (1.10) Коэффициенты скоса пазов для высших гармонических меньше, чем для первой гармонической, поэтому скос пазов также способствует приближению формы кривой МДС к синусоидальной. Обмоточный коэффициент. Произведение коэффициентов распределения, укорочения шага и скоса пазов называют обмоточным коэффициентом. Следовательно, обмоточный коэффициент для ν-й гармонической kоб ν =kpν kcν kyν. (1.11) Этот коэффициент показывает, насколько уменьшается МДС обмотки переменного тока вследствие ее распределения по нескольким пазам, укорочения шага и скоса пазов по сравнению с сосредоточенной обмоткой. Ниже приведены значения коэффициентов распределения k р, укорочения шага k уи обмоточного коэффициента k об, вычисленных для обмотки, имеющей q = 3; α = 20°; у/τ = 7/9. Распределение обмотки по нескольким пазам, укорочение ее шага и скос пазов позволяют получить приблизительно синусоидальное распределение МДС обмотки вдоль окружности статора (или ротора). Так, например, из данных, приведенных выше, следует, что при q = 3, α = 20° и уτ = 7/9 амплитудные значения высших гармонических МДС весьма малы по сравнению с первой гармонической МДС. Их отношения для пятой, седьмой и девятой гармонических составляют: F5/F1 = (1/5)kоб5/kоб1 = 0,0084; F7/F1 = (1/7)kоб7/kоб1 = 0,025; F9/F1 = (1/9)kоб9/kоб1 = 0,041.
Третья гармоническая МДС имеет наибольшее значение: F3/F1 = (1/3)kоб3/kоб1 = 0,123. Однако, как будет показано создаваемые ею третьи гармонические ЭДС при соединении фазных обмоток электрической машины по схеме «звезда» не оказывают существенного влияния на работу машины и не выходят во внешнюю сеть. Поэтому практически стремятся уменьшить главным образом пятую и седьмую гармонические МДС, применяя шаг обмотки у ≈ 0,8τ.
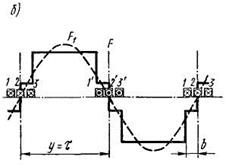
ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ Пульсирующее поле. При питаний однофазной обмотки переменным током возникает магнитное поле, пульсирующее во времени с частотой изменения тока. В этом случае при синусоидальном распределении МДС (рис. 1.12) в каждой точке воздушного зазора, расположенной на расстоянии х от оси обмотки, действует МДС Fx = F0 cos(πx/τ) = Fm sinωt cos(πx/τ), (1.12) где F 0 = F msin ωt — МДС в точке, расположенной на оси обмотки. Выражение (1.12) можно преобразовать к виду Fx = 0,5Fm sin(ωt-πx/τ) + 0,5Fm sin(ωt+πx/τ). (1.13) Каждый из членов правой части (1.13) представляет собой уравнение бегущей (или вращающейся) волны МДС. Следовательно, пульсирующее магнитное поле, синусоидально распределенное в пространстве, можно представить в виде суммы двух магнитных полей, вращающихся в противоположных направлениях (рис. 1.13). При этом бегущие волны МДС, создающие эти магнитные поля. F΄x = 0,5Fm sin(ωt-πx/τ); F˝x = 0,5Fm sin(ωt+πx/τ).(1.14)
Рис. 1.12 - Диаграмма распределения МДС в воздушном зазоре (а) и годографы пространственного вектора МДС (б, в)
Рис. 1.13 - Вращающиеся магнитные поля однофазной обмотки
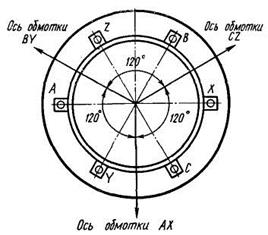
В каждом из этих полей максимальные значения МДС в различные моменты времени остаются неизменными. Следовательно, если каждое из этих полей представить в виде пространственного вектора МДС В качестве положительного направления условно примем направление вращения бегущей волны МДС по часовой стрелке. Координату точки х, в которой МДС F' xмаксимальна и равна 0,5F m, можно получить, положив sin (ωt π х/τ) = 1. При этом ωt — π х/τ = π/2, откуда x=τ(ωT-π/2)/π.(1.15) Следовательно, при увеличении угла ωt координата точки х перемещается в положительном направлении, т. е. МДС F' xвращается по часовой стрелке, a F′' x — против часовой стрелки. Линейная скорость перемещения бегущей волны МДС ν = dx/dt = ωT/π = 2fτ, (1.16) т. е. за один период магнитное поле проходит пару полюсов. Частота вращения бегущей волны МДС (частота вращения магнитного поля) n1 = 60υ/(πD) = 60·2fτ/(πD) = 60f/p. (1.17) Следовательно, изменяя число полюсов электрической машины 2р, можно получать различные частоты вращения магнитного поля. Из (1.17) следует, что в многополюсной машине за один период изменения переменного тока магнитное поле поворачивается на пространственный угол 360°/ p, соответствующий одной паре полюсов. Поэтому при рассмотрении электромагнитных процессов в электрических машинах вводят понятие «электрические градусы», с которыми оперируют при построении векторных диаграмм, проектировании обмоток и пр. При этом 360 временным градусам соответствует 360р электрических градуса, а электрические градусы имеют связь с геометрическими градусами в виде соотношения α˚эл= p α˚геом. Если на статоре электрической машины расположить симметричную трехфазную обмотку (рис. 1.14), у которой оси фаз АХ, BY и CZ сдвинуты в пространстве на угол 120˚, то при питании ее симметричным трехфазным током получим круговое вращающееся магнитное поле. На рис. 1.14 для простоты фазы обмотки показаны сосредоточенными, но распределение МДС, образуемое каждой фазой, следует считать синусоидальным. Ввиду того, что в рассматриваемой обмотке фазы АХ, BY и CZ смещены в пространстве на (2/3) τ, а токи вних сдвинуты во времени на угол (2/3) π, получим следующие выражения для составляющих МДС в точке х от каждой из фаз:
Рис. 1.14 - Расположение обмоток фаз на статоре двухполюсной трехфазной машины
Результирующую МДС в точке х можно получить путем сложения отдельных ее составляющих F xА, F xB, F xC. При этом обратновращающиеся волны МДС исчезают, а результирующая МДС Fx рез = 1,5Fm sin(ωt-πx/τ). (1.18)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.143.150 (0.01 с.) |

 )Iw(4/π)[cosπx/τ + (1/3)cos3πx/τ +
)Iw(4/π)[cosπx/τ + (1/3)cos3πx/τ + π)Iw ≈ 0,9Iw. (1.4)
π)Iw ≈ 0,9Iw. (1.4)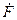 п1x,
п1x, 



 и
и  указанных обмоток (рис. 1.11, в), значение которых при максимальном значении тока в фазе равно F′ 1 = F′' 1 = 0, 45Iwk р1. При этом
указанных обмоток (рис. 1.11, в), значение которых при максимальном значении тока в фазе равно F′ 1 = F′' 1 = 0, 45Iwk р1. При этом

 (рис. 1.12, б), то конец его будет описывать окружность. Такое поле называют круговым.
(рис. 1.12, б), то конец его будет описывать окружность. Такое поле называют круговым. ;
; ;
; .
.