
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гаусса с выбором главного элементаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Решим следующую СЛАУ методом Гаусса.
где a= Конечная разрядность компьютера предполагает неизбежные округления. Будем считать, что наш компьютер при округлении получает a»1. Поэтому обратный ход дает X2=1, X1=104 - 104 = 0, т.е. вектор решения получается X= Переставим уравнения в исходной системе местами, тогда имеем:
Точное решение задачи
Принципиальное отличие между этими двумя случаями заключается в том, что при перестановке уравнений ведущие элементы оказываются одного порядка, в то время как без перестановки они несопоставимы по порядкам. Именно это обстоятельство приводит к потере значащих цифр при округлении. Поэтому прямой ход в методе исключения непременно должен включать в себя стратегию выбора ведущего элемента, фиксируемого на главной диагонали. Например, в стратегии частичного упорядочивания ведущий элемент выбирается как максимальный по модулю в k -ом столбце на k -ом шаге исключения: akk=max½aik½ для k £ i £ n. Такая модификация носит название метода Гаусса с выбором максимального элемента по столбцу. Возможны также варианты выбора максимального элемента по строке и по всей матрице, но они связаны с дополнительными сложностями в реализации алгоритмов.
Решение систем линейных алгебраических уравнений методом прогонки.
Метод прогонки для решения систем с трёхдиагональной матрицей Часто возникает необходимость в решении систем, матрицы которых, являясь слабозаполненными, т.е. содержащими много ненулевых элементов. Матрицы таких систем обычно имеют определенную структуру, среди которых выделяют системы с матрицами ленточной структуры, т.е. в них ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами метод Гаусса можно трансформировать в более эффективные методы. Рассмотрим наиболее простой случай ленточных систем, к которым, как мы увидим впоследствии, сводится решение задач дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др. Трёхдиагональной матрицей называется такая матрица, у которой ненулевые элементы стоят только на главной диагонали и соседних с ней:
У трёхдиагональной матрицы ненулевых элементов всего (3n-2). Переобозначим коэффициенты матрицы:
Тогда в покомпонентной записи систему можно представить в виде: ai * xi-1 + bi * xi + ci * xi+1 = di, i=1, 2,…, n; (7) a1=0, cn=0. (8) Структура системы предполагает взаимосвязь только между соседними неизвестными: xi=xi *xi+1+hi (9) Уменьшим в представлении (9) индекс на единицу: xi-1=xi-1*xi + hi-1 и подставим в (7): ai(xi-1*xi + hi-1)+ bi * xi + ci * xi+1 = di (ai *xi-1 + bi )xi = –ci * xi+1 +di –ai * hi-1 Сравнивая полученное выражение с представлением (7), получаем: Формулы (10) представляют реккурентные соотношения для вычисления коэффициентов прогонки. Они требуют задания начальных значений. В соответствии с первым условием (8) для i =1 имеем a1=0, а значит
Далее вычисляются и сохраняются остальные прогоночные коэффициенты по формулам (10) для i=2,3,…, n, причем при i=n, с учетом второго условия (8), получаем xn=0. Следовательно, в соответствии с формулой (9) xn = hn. После чего по формуле (9) последовательно находятся неизвестные xn-1, xn-2, …, x1. Этот этап расчета называется обратным ходом, в то время как вычисление прогоночных коэффициентов называется прямым ходом прогонки. Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при большой размерности систем не должно быть быстрого роста погрешностей округления. Будем называть прогонку корректной, если знаменатель прогоночных коэффициентов (10) не обращается в ноль, и устойчивой, если ½xi½<1 при всех i=1,2,…, n. Достаточные условия корректности и устойчивости прогонки, которые во многих приложениях выполняются, определяются теоремой. Теорема. Пусть коэффициенты ai и ci уравнения (7) при i=2,3,..., n-1 отличны от нуля и пусть ½bi½>½ai½+½ci½ при i=1, 2,..., n. (11) Тогда прогонка, определяемая формулами (10), (9) корректна и устойчива.
Алгоритм метода прогонки.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.01 с.) |


 ,
,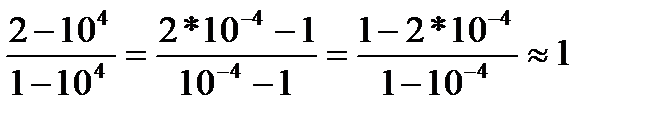 .
. - неверный результат.
- неверный результат. .
.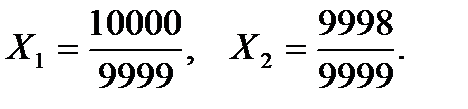
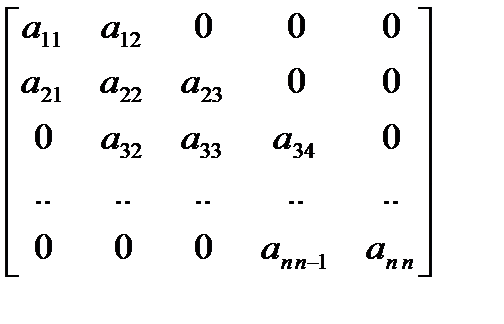
 .
.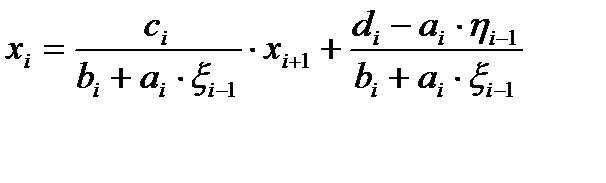

 (10)
(10)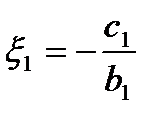 ,
, 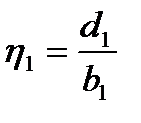 .
.


