
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм и его свойства (рассмотреть алгоритм умножения).Содержание книги
Поиск на нашем сайте
Алгоритм и его свойства (рассмотреть алгоритм умножения). Алгоритмом называется точная инструкция исполнителю в понятной для него форме, определяющая процесс достижения поставленной цели на основе имеющихся исходных данных за конечное число шагов. Основными свойствами алгоритмов являются: 1. Универсальность (массовость) - применимость алгоритма к различным наборам исходных данных. 2. Дискретность - процесс решения задачи по алгоритму разбит на отдельные действия. 3. Однозначность - правила и порядок выполнения действий алгоритма имеют единственное толкование. 4. Конечность - каждое из действий и весь алгоритм в целом обязательно завершаются. 5. Результативность - по завершении выполнения алгоритма обязательно получается конечный результат. 6. Выполнимость - результата алгоритма достигается за конечное число шагов. Алгоритм считается правильным, если его выполнение дает правильный результат. Соответственно алгоритм содержит ошибки, если можно указать такие допустимые исходные данные или условия, при которых выполнение алгоритма либо не завершится вообще, либо не будет получено никаких результатов, либо полученные результаты окажутся неправильными. Выделяют три крупных класса алгоритмов: · вычислительные алгоритмы, работающие со сравнительно простыми видами данных, такими как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным; · информационные алгоритмы, представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных); · управляющие алгоритмы, генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют. Алгоритм умножения Есть А и N- целые числа(параметры задачи) А*N=>М 1.Присвоить I значение 0 2.Присвоить Р значение 0 3.Проверка. Если А или N=0, то перейти к шагу 7 4.Присвоить Р значение Р+А 5.Присвоить значение I+1 6.Если I меньше N, то перейти к шагу 4 7.Присвоить М значение Р 8.Конец
Языки программирования. Язык программирования – система обозначений для описания программ. Обычный разговорный язык состоит из четырех основных элементов: символов, слов, словосочетаний и предложений. Алгоритмический язык содержит подобные элементы, только слова называют элементарными конструкциями, словосочетания - выражениями, предложения - операторами. Алгоритмический язык (как и любой другой язык), образуют три его составляющие: алфавит, синтаксис и семантика.
Алфавит – фиксированный для данного языка набор символов (букв, цифр, специальных знаков и т.д.), которые могут быть использованы при написании программы. Синтаксис - правила построения из символов алфавита специальных конструкций, с помощью которых составляется алгоритм. Семантика - система правил толкования конструкций языка. Таким образом, программа составляется с помощью соединения символов алфавита в соответствии с синтаксическими правилами и с учетом правил семантики.
Существуют различные классификации языков программирования. Все языки программирования делят на языки низкого, высокого и сверхвысокого уровня. В группу языков низкого уровня входят машинные языки и языки символического кодирования: (Автокод, Ассемблер). Операторы этого языка – это те же машинные команды, но записанные мнемоническими кодами, а в качестве операндов используются не конкретные адреса, а символические имена. Все языки низкого уровня ориентированы на определенный тип компьютера, т. е. являются машинно-зависимыми. Машинно-ориентированные языки – это языки, наборы операторов и изобразительные средства которых существенно зависят от особенностей ЭВМ (внутреннего языка, структуры памяти и т.д.). Следующую, существенно более многочисленную группу составляют языки программирования высокого уровня. Это Фортран, Алгол, Кобол, Паскаль, Бейсик, Си, Пролог и т.д. Эти языки машинно-независимы, т.к. они ориентированы не на систему команд той или иной ЭВМ, а на систему операндов, характерных для записи определенного класса алгоритмов. Однако программы, написанные на языках высокого уровня, занимают больше памяти и медленнее выполняются, чем программы на машинных языках. К языкам сверхвысокого уровня можно отнести лишь Алгол-68 и APL. Повышение уровня этих языков произошло за счет введения сверхмощных операций и операторов.
Разветвляющиеся алгоритмы. Алгоритм вычисления арксинуса - агсsin х.
В таких алгоритмах делается выбор: выполнять или не выполнять какую-нибудь группу команд в зависимости от условия, т.е. выбирается один из нескольких возможных путей (вариантов) вычислительного процесса. Каждый подобный путь называется ветвью алгоритма. Признаком разветвляющегося алгоритма является наличие операций условного перехода, когда происходит проверка истинности некоторого логического выражения (проверяемое условие) и в зависимости от истинности или ложности проверяемого условия для выполнения выбирается та или иная ветвь алгоритма. В логических выражениях используется операция сравнения: < (меньше), > (больше), <= (меньше или равно), >= (больше или равно), = (равно), <> (не равно). Часто встречаются задачи, в которых используются не отдельные условия, а совокупность связанных между собой условий (отношений). Для связи используются AND и (или) OR. Арксинус(х). Алгоритм А)Если |x|<1, то арксин(х) Б)Если |x|=1, то арксин(х)=sign(x) В)Если |x|>1, то вывести сообщение об ошибке.
Программа вычисления арксинуса - Агcsin. Program ArcSin; Uses сrt; Const one=’------------------------‘; two=’------------------------‘; nl=#13#10; Var x,t,ypribl,ycontr:real; Begin Clrscr; Write(‘Введите x==>’); Readln(x); Clrscr; Writeln(nl,nl,two,nl,’Вычисление arcsin’, Nl,’ x=’,x:7:3); If abs(x)<1 Then begin t:=x*x; ypribl:=(((5*t/112+3/40)*t+1/6)*t+1)*x; end; else if abs(x)>1 then begin writeln(‘Ошибка!’); halt end; else if x=1 then ypribl:=pi*0.5; else ypribl:=-pi*0.5; if abs(x)=1 then y contr:=ypribl else ycontr:=arctan(x/sqrt(1-x*x)); writeln(nl,one,nl,’ Ответы:’, nl,’ ypribl=’,ypribl:>:4, nl,’ ycontr=’,ycontr:z:4, nl,two,nl,’Press Enter!’:40); readln; end.
5. Программа расчета машинного "эпсилона" - Ерsilon. Program Epsilon; {Программа вычисляет и выводит на экран значение "машинного эпсилон"} Var; epsilon: Real; begin epsilon:= 1; while epsilon/2 + 1 > 1 do epsilon:= epsilon/2; WriteLn('Машинное эпсилон = ',epsilon); Readln; end.
6. Циклические алгоритмы. Программа вычисления конечного произведения (степени числа а). Алгоритмы, содержащие команды повторения, называют циклическими. Команды повторения составляют цикл. Цикл - это такая форма организации действий, при которой одна последовательность действий повторяется несколько раз (или не разу), до тех пор, пока выполняются некоторые условия. Цикл с параметром, предусловием и постусловием. Программа вычисления конечного произведения (степени числа а). Program Production; Uses сrt; Const nl=#13#10; one=’------------------------‘; Var a,p:real; i,n:integer; Begin Clrscr; Write(‘Введите основание и показатель степени ==>’); Readln(a,n); Clrscr; Writeln(nl,nl,one,nl,’Введите число а ’, a:6:2,’ в степени’, n:3,’ даёт: ‘); If n=0 Then p:=1 else begin p:=a; for i:=2 to abs(n) do p:=p*a; if n<0 then p:=1/p; end; writeln(p:9:2,nl,one,nl,‘Нажмите клавишу «Enter»!’); readln; end.
Программа вычисления гипотенуз с использованием функции Роwer. Program Using Function; Uses сrt; Const nl=#13#10; one=’------------------------‘; Var a,b,hyp:real; i:integer; Function Power(a:real; n:integer):real; Var i:integer; res:real; begin if n=0 then power:=1 else begin res:=a for i:=2 to abs(n) do res:=res*a; if n>0 then power:=res else power:=1/res; end; {power} Begin Clrscr; Write(‘Введите катет а ==>’); Readln(a); Clrscr; b:=a*0.25; for i:=1 to 5 do begin hyp:=sqrt(power(a,2)+power(b,2)); writeln(i:2, a:7:2, b:7:2, hyp:9:2); end; writeln(‘Press Enter!’:20); readln; end.
Процедура РrintLine и ее использование в программах.
Метод хорд Допустим, что на [a,b] функция f(x) меняется почти линейно. Тогда ее можно заменить стягивающей хордой y(x):
Точку пересечения хорды с осью абсцисс, где y(x1)=0 примем за первое приближение к корню исходного уравнения x1=a- Аналогично x2=x1- Обобщая, получим расчетную формулу xn+1=xn- где X―неподвижный конец интервала. Для сходимости метода должны быть выполнены все условия теоремы о сходимости метода Ньютона, только условие f(X)•f"(X)>0 определяет выбор неподвижного конца; противоположный конец берется за начальное приближение: f(x0)•f "(x0)<0. Геометрическая интерпретация метода хорд показана на рис.4.
ƒ(b) y
ƒ(х)
0 a x1 x2 ξ b x ƒ(a)
Пусть b+δb= Для оценок возьмем норму-максимум. ||δb||/||b||=0.000106/1.989903≈0.000053 x+δx= Таким образом (||δx||/||x||)/(||δb||/||b||)=2/0.000053≈40000≤cond(A). В данном примере полученное значение совпадает с коэффициентом обусловленности.
Алгоритм метода Гаусса.
Алгоритм метода прогонки.
Алгоритм метода Зейделя. Исходные данные: А – квадратная матрица коэффициентов порядка n, b – столбец свободных членов, х(0)- столбец начальных значений, n – порядок системы, kmax- предельное число итераций (страховка от зацикливания), e - требуемая точность. Результаты: х – вектор решений,
begin
i=1,n
xi←xi(0) pi←1/aii
k=1,kmax
kend←k
i=1,n
t←bi
j=1,n
i¹j
t=t-aijx
xnew←t*pi
½xnew-xi½>g
kend=0
xi← xnew
kend¹0
exit
end
kend – фактическое количество итераций (если достигнута точность e), если точность не достигнута за. kmax итераций, то kend= 0. Вспомогательные переменные: t – переменная суммирования для накопления очередной компоненты, xnew – переменная для временного хранения очередной компоненты решения в новом приближении. Тело алгоритма состоит из двух последовательных циклов: первый играет вспомогательную роль (назначает начальные значения элементам столбца из неизвестных, вычисляет обратные величины диагональных элементов), второй – он троекратный, реализует процесс Зейделя. Во внешнем цикле (цикл «по ε») меняется значение счётчика k от единицы с шагом, равным единице, до заданного предельного числа итераций kmax. В конце его при истинном неравенстве |xi(k+1)-x(k)i|≤ε (тогда kend=0) выполняется возврат к точке вызова данного алгоритма. В цикле «по строкам» (цикл «по i») вычисляются компоненты очередного приближения xi(k+1) (которые предварительно записываются в переменной xnew) и анализируется условие |xi(k+1)-xi(k)|≤. Если хотя бы для одной компоненты оно не выполняется, то переменной kend присваивается нуль. Самый внутренний цикл (цикл «по j») служит для для реализации вычислений по формуле (15); в нем из правых частей уравнений системы (16) вычитаются левые части, содержащие все неизвестные кроме i- го.
Алгоритм и его свойства (рассмотреть алгоритм умножения). Алгоритмом называется точная инструкция исполнителю в понятной для него форме, определяющая процесс достижения поставленной цели на основе имеющихся исходных данных за конечное число шагов. Основными свойствами алгоритмов являются: 1. Универсальность (массовость) - применимость алгоритма к различным наборам исходных данных. 2. Дискретность - процесс решения задачи по алгоритму разбит на отдельные действия. 3. Однозначность - правила и порядок выполнения действий алгоритма имеют единственное толкование. 4. Конечность - каждое из действий и весь алгоритм в целом обязательно завершаются. 5. Результативность - по завершении выполнения алгоритма обязательно получается конечный результат. 6. Выполнимость - результата алгоритма достигается за конечное число шагов. Алгоритм считается правильным, если его выполнение дает правильный результат. Соответственно алгоритм содержит ошибки, если можно указать такие допустимые исходные данные или условия, при которых выполнение алгоритма либо не завершится вообще, либо не будет получено никаких результатов, либо полученные результаты окажутся неправильными. Выделяют три крупных класса алгоритмов: · вычислительные алгоритмы, работающие со сравнительно простыми видами данных, такими как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным; · информационные алгоритмы, представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных); · управляющие алгоритмы, генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют. Алгоритм умножения Есть А и N- целые числа(параметры задачи) А*N=>М 1.Присвоить I значение 0 2.Присвоить Р значение 0 3.Проверка. Если А или N=0, то перейти к шагу 7 4.Присвоить Р значение Р+А 5.Присвоить значение I+1 6.Если I меньше N, то перейти к шагу 4 7.Присвоить М значение Р 8.Конец
Языки программирования. Язык программирования – система обозначений для описания программ. Обычный разговорный язык состоит из четырех основных элементов: символов, слов, словосочетаний и предложений. Алгоритмический язык содержит подобные элементы, только слова называют элементарными конструкциями, словосочетания - выражениями, предложения - операторами. Алгоритмический язык (как и любой другой язык), образуют три его составляющие: алфавит, синтаксис и семантика. Алфавит – фиксированный для данного языка набор символов (букв, цифр, специальных знаков и т.д.), которые могут быть использованы при написании программы.
Синтаксис - правила построения из символов алфавита специальных конструкций, с помощью которых составляется алгоритм. Семантика - система правил толкования конструкций языка. Таким образом, программа составляется с помощью соединения символов алфавита в соответствии с синтаксическими правилами и с учетом правил семантики.
Существуют различные классификации языков программирования. Все языки программирования делят на языки низкого, высокого и сверхвысокого уровня. В группу языков низкого уровня входят машинные языки и языки символического кодирования: (Автокод, Ассемблер). Операторы этого языка – это те же машинные команды, но записанные мнемоническими кодами, а в качестве операндов используются не конкретные адреса, а символические имена. Все языки низкого уровня ориентированы на определенный тип компьютера, т. е. являются машинно-зависимыми. Машинно-ориентированные языки – это языки, наборы операторов и изобразительные средства которых существенно зависят от особенностей ЭВМ (внутреннего языка, структуры памяти и т.д.). Следующую, существенно более многочисленную группу составляют языки программирования высокого уровня. Это Фортран, Алгол, Кобол, Паскаль, Бейсик, Си, Пролог и т.д. Эти языки машинно-независимы, т.к. они ориентированы не на систему команд той или иной ЭВМ, а на систему операндов, характерных для записи определенного класса алгоритмов. Однако программы, написанные на языках высокого уровня, занимают больше памяти и медленнее выполняются, чем программы на машинных языках. К языкам сверхвысокого уровня можно отнести лишь Алгол-68 и APL. Повышение уровня этих языков произошло за счет введения сверхмощных операций и операторов.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.79 (0.012 с.) |

 =
=  .
. .
. .
. ,
, , т.е. δb=
, т.е. δb= 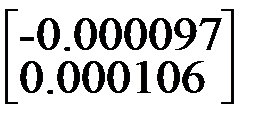
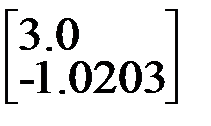 Þ ||δx||/||x||=2/1=2
Þ ||δx||/||x||=2/1=2


