
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод простой итерации для решения систем линейных алгебраических уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как уже было сказано, в итерационных методах определяется не само решение задачи Ax=b, а некоторая последовательность векторов x(k) (k - номер итерации), такая, что она стремится к ветору решения при k®¥. Чтобы построить такую последовательность, надо прежде всего исходную систему Ax=b преобразовать к виду x=Bx+f. (12) Сделать это можно различными способами. Самый простой и распространенный – это выражение каждого диагонального неизвестного из соответствующего по номеру уравнения системы:
т.е. преобразованные матрица B и вектор f имеют вид
Задаваясь начальным приближением – вектором x(0)=(x1(0), x1(0),…., x1(0),), получаем
Такая формула вычисления приближений определяет метод простой итерации – МПИ. Основной вопрос – будет ли последовательность векторов x(k) сходится к решению системы линейных уравнений.
Сходимость последовательности векторов и матричной прогрессии.
Сходимость метода простой итерации для решения систем линейных уравнений
Сходимость последовательности векторов x(0), x(1),…., x(k),…, определяют двумя способами: по компонентам и по норме. Определение 1. Вектор x*=(x1*, x2*,…., xn*,) называется пределом этой последовательности векторов, если существует каждый из n числовых пределов Определенная таким образом сходимость называется сходимостью по компонентам. Определение 2. Последовательность векторов сходится к вектору x* по норме, если Сходимость по норме более общая, так как не зависит от того, будет ли векторное пространство конечной или бесконечной размерности. Если размерность имеет конечное значение n, то сходимость по норме и сходимость по компонентам равносильны (т.е. из одной следует другая). Сходимость по норме во многих случаях более удобна, чем сходимость по компонентам. Все эти рассуждения распространяются и на последовательность матриц B(0), B(1), …, B(k), …, однако здесь нас будет интересовать последовательность степеней матриц E, B, B2, …, Bk, …, называемая матричной геометрической прогрессией. Лемма 1(лемма Неймана). Условие, что все собственные числа матрицы B по модулю меньше единицы, является необходимым и достаточным для того, чтобы 1) Bk®¥ при k®¥; 2) матрица E-B имела обратную и E + B + B2 + … +Bk + …= (E-B)-1. Лемма 2. Если норма ççBçç£q<1 то матрица E–B имеет обратную (E–B)-1 = E + B + B2 + … +Bk + …, причем Доказательство: Обозначим матрицу, которая представляет сумму ряда степеней матрицы B за V:
Пронормируем это выражение и воспользуемся свойствами нормы:
Так как (E-B)V=(E + B + B2 + … + Bk + …) - (B + B2 + … + Bk+1 + …) = E, то V=(E-B)-1, и следовательно
Лемма 2 доказана. Теорема 1 (о сходимости МПИ). Необходимым и достаточным условием сходимости МПИ при любом начальном векторе x(0) к решению x* СЛАУ x=Bx+f является требование, чтобы все собственные значения матрицы B по модулю были меньше единицы. Докажем только достаточность. Пусть собственные значения матрицы B по модулю были меньше единицы max½li(B)½<1, i=1,2,…, n. По лемме 1 имеем Bk®¥ при k®¥, а также E + B + B2 + … + Bk + …= (E+B)-1. Применяя последовательно формулу МПИ для вычисления приближений: x(1)=Bx(0)+f, x(2)=Bx(1)+f=B(Bx(0)+f)+f=B2x(0)+(E+B)f, .......... x(k+1)=Bk+1x(0) + (E + B + B2 + … + Bk)f. 0 ( Правая часть последнего выражения при любом x(0) и Представим исходную систему x=Bx+f в виде (E-B)x=f и подставим x*: (E-B)(E-B)-1f=f. Получается, что x* действительно является решением системы уравнений. Достаточность доказана. Вспоминая соотношение между собственными значениями и нормами матриц, можно сформулировать достаточный признак устойчивости: Для сходимости МПИ достаточно, чтобы какая-либо норма матрицы B была меньше единицы. Некоторые квадратные матрицы обладают свойством, называемым диагональным преобладанием. Это означает, что диагональные элементы по модулю больше суммы модулей всех остальных элемнтов в данной строке:
Для изложенного способа преобразования системы к итерационному виду справедливо утверждение: в случае диагонального преобладания в исходной матрице A метод простой итерации сходится.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.191 (0.007 с.) |

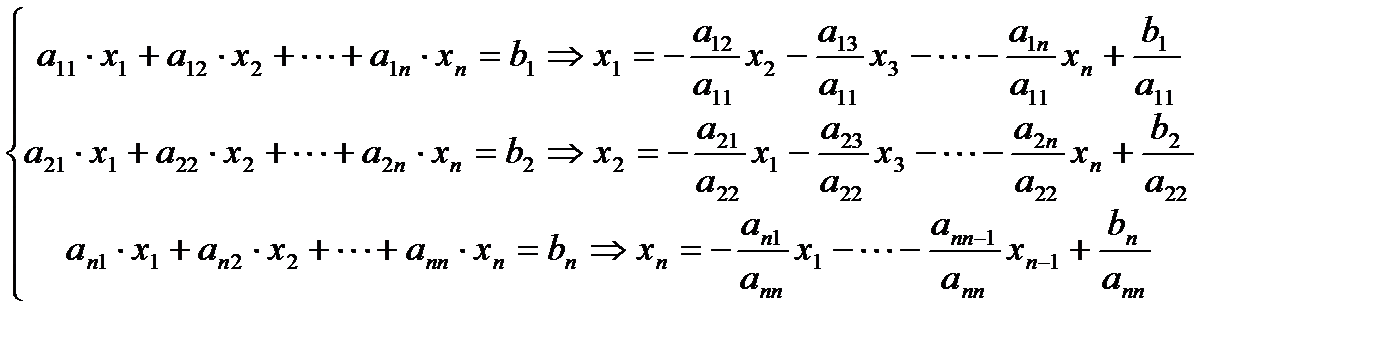
 , f=
, f=  .
. (13)
(13)
 .
. .
. .
.
 .
. )
) .
. . (14)
. (14)


