
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценки погрешности метода простой итерации для решения систем уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема 2. (о погрешностях приближения в МПИ) Пусть ççBçç£q<1. Тогда справедливы оценки погрешности:
x(k+1)=Bx(k)+f, x(k)=Bx(k-1)+f. Возьмем разность между этими приближениями: x(k+1)- x(k)=Bx(k)- Bx(k-1)= B(x(k)- x(k-1)) и про
Из последнего неравенства (*) видно в силу условия q<1, что элементы итерационной последовательности сближаются с ростом номера k. Оценим разность между (k+m) -ым и k -м членами последовательности при m>0:
Устремляя при фиксированном k
Используя вновь соотношение (*), получим
откуда и получается априорная оценка погрешности:
Теорема 2 доказана.
Метод Зейделя для решения систем линейных алгебраических уравнений.
При вычислении очередного (k+1)- го приближения в МПИ в правую часть расчетной формулы (13) подставляется предыдущее, k- ое приближение, т.е. вектор x(k), все компоненты которого имеют одинаковый итерационный индекс: (x1(k), x2(k),…, xn(k)). Однако элементы вектора вычисляются последовательно, поэтому, например, при вычислении x2(k+1) уже вычислен x1(k+1) в новом приближении. Метод, в котором для подсчета i-ой компоненты (k+1)- ого приближения используются уже найденные на этом, т.е. (k+1) -м шаге, новые значения первых i-1 компонент, называется методом Зейделя. Если приведение системы к итерационному виду сделано как это описано в предыдущем параграфе, то расчетная формула для элементов решения
В развернутом виде метод Зейделя определяется системой равенств: x1(k+1) = (b1-a12x2(k)-a13x3(k)-…-a1nxn(k))/a11, x2(k+1)= (b2-a21x1(k+1)-a23x3(k)-…-a2nxn(k))/a22, …………………………………………… (16) xn(k+1) = (bn-an1x1(k+1)-an2x2(k+1)-…-an,n-1xn-1(k+21))/ann. В сравнении с МПИ метод Зейделя сходится быстрее. Кроме того, при его реализации на компьютере не нужен отдельный массив для хранения нового приближения. Вычисленные компоненты нового вектора x(k+1) заносятся на место соответствующих компонент старого вектора x(k), в этой связи метод Зейделя называют методом последовательных смещений. В МПИ нужно целиком сохранять массив значений x(k), подставляемый в правую часть расчетной формулы (13), до тех пор, пока не сформирован полностью новый массив x(k+1) – результат текущего итерационного шага. Поэтому МПИ называют методом одновременных смещений.
Достаточные условия метода Зейделя такие же как и для МПИ. Процесс итераций продолжаем до тех пор, пока значения xi(k+1) (i=1,2,…,n) не станут близким к значениям xi(k) с заданной погрешностью g.
Алгоритм метода Зейделя. Исходные данные: А – квадратная матрица коэффициентов порядка n, b – столбец свободных членов, х(0)- столбец начальных значений, n – порядок системы, kmax- предельное число итераций (страховка от зацикливания), e - требуемая точность. Результаты: х – вектор решений,
begin
i=1,n
xi←xi(0) pi←1/aii
k=1,kmax
kend←k
i=1,n
t←bi
j=1,n
i¹j
t=t-aijx
xnew←t*pi
½xnew-xi½>g
kend=0
xi← xnew
kend¹0
exit
end
kend – фактическое количество итераций (если достигнута точность e), если точность не достигнута за. kmax итераций, то kend= 0. Вспомогательные переменные: t – переменная суммирования для накопления очередной компоненты, xnew – переменная для временного хранения очередной компоненты решения в новом приближении. Тело алгоритма состоит из двух последовательных циклов: первый играет вспомогательную роль (назначает начальные значения элементам столбца из неизвестных, вычисляет обратные величины диагональных элементов), второй – он троекратный, реализует процесс Зейделя. Во внешнем цикле (цикл «по ε») меняется значение счётчика k от единицы с шагом, равным единице, до заданного предельного числа итераций kmax. В конце его при истинном неравенстве |xi(k+1)-x(k)i|≤ε (тогда kend=0) выполняется возврат к точке вызова данного алгоритма. В цикле «по строкам» (цикл «по i») вычисляются компоненты очередного приближения xi(k+1) (которые предварительно записываются в переменной xnew) и анализируется условие |xi(k+1)-xi(k)|≤. Если хотя бы для одной компоненты оно не выполняется, то переменной kend присваивается нуль. Самый внутренний цикл (цикл «по j») служит для для реализации вычислений по формуле (15); в нем из правых частей уравнений системы (16) вычитаются левые части, содержащие все неизвестные кроме i- го.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1735; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.20.13 (0.01 с.) |

 , (апостериорная оценка)
, (апостериорная оценка) . (априорная оценка)
. (априорная оценка)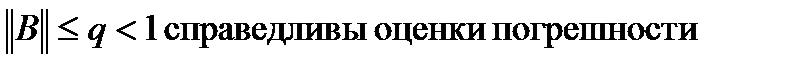 Доказательство: Рассмотрим два соседних приближения:
Доказательство: Рассмотрим два соседних приближения: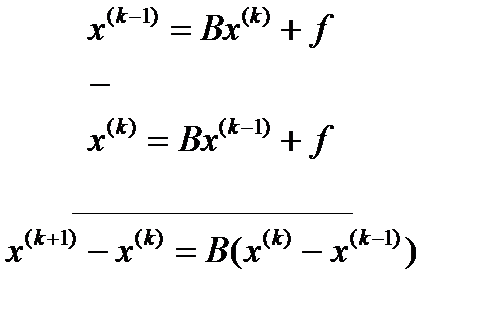 нормируем это выражение:
нормируем это выражение: ,
, . (*)
. (*)
 , т.е.
, т.е.
 , i=1,2,…, n. (15)
, i=1,2,…, n. (15)


