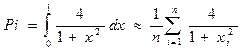Многопроцессорные системы с индивидуальной памятью или

Массивно-параллельные системы (MPP)

Проблема масштабируемости решается в системах с распределенной (индивидуальной) памятью (рисунок), в которых число процессоров практически не ограничено.

 

Сетевой закон Амдала. Главным фактором, снижающим эффективность

таких машин, является потери времени на передачу сообщений.

Одной из главных характеристик параллельных систем является ускорение R параллельной системы, которое определяется выражением:

R = T 1 / Tn,

где T1 − время решения задачи на однопроцессорной системе, а Tn − время ре-

шения той же задачи на n − процессорной системе.

Пусть W = Wск + Wпр, где W − общее число операций в задаче, Wпр −

число операций, которые можно выполнять параллельно, а Wcк − число

скалярных (нераспараллеливаемых) операций. Обозначим также через t время

выполнения одной операции. Тогда получаем известный закон Амдала:

 

Здесь a = W ск / W − удельный вес скалярных операций.

Основной вариант закона Амдала не отражает потерь времени на меж-

процессорный обмен сообщениями. Перепишем закон Амдала:

Здесь W c − количество передач данных, t c − время одной передачи данных.

 

Это выражение

 

и является сетевым законом Амдала. Этот закон определяет следующие две

особенности многопроцессорных вычислений:

Коэффициент сетевой деградации вычислений с:

определяет объем вычислений, приходящийся на одну передачу данных (по

затратам времени). При этом сА определяет алгоритмическую составляющую

коэффициента деградации, обусловленную свойствами алгоритма, а сТ − техни-

ческую составляющую, которая зависит от соотношения технического быстро-

действия процессора и аппаратуры сети.

В некоторых случаях используется еще один параметр для измерения эффективности вычислений – коэффициент утилизации z:

 

Программирование для систем с передачей сообщений. Наиболее распространенной библиотекой параллельного программирования в модели передачи сообщений является MPI (Message Passing Interface). MPI является биб-

лиотекой функций межпроцессорного обмена сообщениями и содержит около

300 функций.

Эффективность систем с обменом сообщениями определяется качеством параллельного алгоритма. Если в нем нет параллелизма, то ЭВМ с множеством

процессоров будет работать даже медленнее однопроцессорной ЭВМ.

Пример параллельных ЭВМ с обменом сообщениями.

Архитектура. Система состоит из однородных вычислительных узлов, включающих:

• один или несколько центральных процессоров (обычно RISC),

• локальную память (прямой доступ к памяти других узлов невозможен),

• коммуникационный процессор или сетевой адаптер,

• иногда - жесткие диски (как в SP) и/или другие устройства В/В.

К системе могут быть добавлены специальные узлы ввода-вывода и управляющие узлы. Узлы связаны через некоторую коммуникационную среду (высокоскоростная сеть, коммутатор и т.п.)

Примеры. IBM RS/6000 SP2, Intel PARAGON/ASCI Red, CRAY T3E, Hitachi SR8000, транспьютерные системы Parsytec.

Масштабируемость. Общее число процессоров в реальных системах достигает нескольких тысяч (ASCI Red, Blue Mountain).

Операционная система. Существуют два основных варианта:

1. Полноценная ОС работает только на управляющей машине (front-end), на каждом узле работает сильно урезанный вариант ОС, обеспечивающие

только работу расположенной в нем ветви параллельного приложения.

Пример: Cray T3E.

2. На каждом узле работает полноценная UNIX-подобная ОС (вариант,

близкий к кластерному подходу). Пример: IBM RS/6000 SP + ОС AIX, устанавливаемая отдельно на каждом узле.

 

СРЕДСТВА ПАРАЛЛЕЛЬНОГО ПРОГРАММИРОВАНИЯ

Параллельные алгоритмы

Вычислительные алгоритмы обладают различным уровнем параллелизма.

Для некоторых классов задач имеется качественная оценка величины паралле-

лизма. Некоторые результаты такой оценки представлены в следующей таблице

Характеристики некоторых параллельных алгоритмов

№	Наименование алгоритма	Время вычислений	Число процессов
	Алгебра Решение треугольной системы уравнений, обращение треугольной матрицы Вычисление коэффициентов характеристического уравнения матрицы Решение системы линейных уравнений, обращение матрицы Метод исключения Гаусса Вычисление ранга матрицы Подобие двух матриц Нахождение LU -разложения симметричной матрицы   Комбинаторика ε —оптимальный рюкзак, n — размерность задачи Задача о покрытии с гарантированной оценкой отклонения не более, чем в (1+ε)log d раз Нахождение ε — хорошей раскраски в задаче о балансировке множеств   Теория графов Ранжирование списка Эйлеров путь в дереве Отыскание дерева минимального веса Транзитивное замыкание Раскраска вершины в Δ + 1 и Δ цветов Дерево поиска в глубину для графа   Сортировка и поиск Сортировка Слияние для двух массивов размера n и m, N = m + m	0(log^2 n)     0(log^2 n)     0(log^2 n)   0(log^2 n) 0(log^2 n) 0(log^2 n) 0(log ^3 n)   0(log n log (n/ ε))   0(log^2 n log m)     0(log^3 n)     0(log n) 0(log n) 0 (log^2 n)   0 (log^2 n) 0(log^3 n loglog n)   0(log^3 n)   0 (log n) 0( + log N)	0(n^4 / log^2 n)     0(n^4 / log^2 n)   0(n ^w^+1) полиномиальное   0(n^4 / log^2 n)   0(n^3 / ε^2)   0(n)     полиномиальное     0(n /log n) 0(n /log n)   0(n + m)   0(n)   0(n) P = 0(N / log N)

 

Скрытый параллелизм. Необходимое условие параллельного выполнения i-й и j-й итераций цикла записывается как и в случае арифметических выражение в виде правила Рассела для циклов:

 

(OUT(i) AND IN(j)) OR (IN(i) AND OUT(j)) OR (OUT(i) AND OUT(j))=0

 

Приведем примеры зависимостей между итерациями – прямая (а), обратная

(б) и конкуренционная (в):

а) Итерация i а (i) = a (i –1) итерация 5 а(5) = а(4)

---------------------------------------

Итерация i+1 a (i + 1) = a (i) итерация 6 а(6) = а(5)

б) Итерация i a (i – 1) = a (i) итерация 5 а(4) = а(5)

--------------------------------------

Итерация i + 1 a (i) = a (i = 1) итерация 6 а(5) = а(6)

в) Итерация i s =

--------------------------------------

Итерация i + 1 s =

Знание оценок из таблицы не дает еще возможности построить практический параллельный алгоритм. Во многих случаях он не очевиден и его еще нужно различными приемами проявить в форме, доступной для программирования на некотором параллельном языке. Пример такого проявления приводится ниже.

Рассмотрим метод гиперплоскостей, предложенный L.Lamport в 1974 году на примере решения уравнений в частных производных. Метод носит название “фронта волны”. Пусть дана программа для вычисления в цикле значения Xi,j как среднего двух смежных точек (слева и сверху):

DO 1 I = 1,N

DO 1 J = 1,N

1 X (I, J) = X (I-1, J) + Y (I, J –1) + C

Рассмотрим две любые смежные по значениям индексов итерации, например:

X(2,2) = X(1,2) + X(2,1)

X(2,3) = X(1,3) + X(2,2)

Между итерациями существует прямая зависимость. Использовать для сложения смежные строки нельзя, так как нижняя строка зависит от верхней. Нельзя складывать и смежные столбцы, так как правый столбец зависит от левого. Тем не менее параллелизм в задаче есть, например, все операции в диагонали 41, 42, 43, 44 можно выполнять параллельно.

Если повернуть оси I, J на 45 градусов и переименовать операции внутри каждой диагонали,как на следующем рисунке, то можно использовать этот параллелизм. Соответствующая программа для верхних диагоналей (включая глав

ную) и нижних диагоналей приведена ниже:

DO 1 I = 1,N Пусть I =3, тогда x(3,1)=x(2,1)+x(3,0)

DO PAR J = 1, I x(3,2)=x(2,2)+x(2,1)

X (I, J) = X(I-1, J) + X(I-1, J-1) x(3,3)=x(2,3)+x(2,2)

1 CONTINUE Эти итерации действительно независимы

---------------------------------------

K + 2

DO 2 I = N +1, 2N – 1

DO PAR J + K, N

R = K + 1

X(I, J) = x(I-1, J) + X(I-1, J-1) + C

2 CONTINUE

Здесь К = 1,2 обозначает левый - верхний или правый - нижний треугольник пространства итераций.

Алгоритм метода гиперплоскостей состоит в следующем:

1. Производится анализ индексов и построение зависимостей в пространстве

итераций

2. Определяется угол наклона осей и переименование переменных

3. Строится параллельная программ

Недостаток метода гиперплоскостей состоит в том, что ширина параллелизма в каждой итерации параллельной программы неодинакова. Это исключено в методе параллелепипедов и ряде других методов.

Для параллельного программирования существует ряд языков. Основные из них:

• OpenMP – для многопроцессорных систем с общей памятью

• MPI - для многопроцессорных систем с индивидуальной памятью

Существует часто некоторая путаница между OpenMP и MPI. Эта путаница вполне понятно, поскольку есть еще версия MPI называется "Open MPI". С точки зрения программиста, MPI является библиотекой, которая содержит процедуры передачи сообщений. OpenMP, с другой стороны, представляет собой набор директив компилятора, которые сообщают OpenMP, если включен компилятор, какие части программы может быть запущены как нити. Таким образом, разница «нити» против «сообщений». Рассмотрим оба метода.

 

ЛЕКЦИЯ 14.

 

Стандарт MPI

Наиболее распространенной библиотекой параллельного программирования в модели передачи сообщений является MPI (Message Passing Interface). Рекомендуемой бесплатной реализацией MPI является пакет MPICH, разработанный в Аргоннской национальной лаборатории.

MPI является библиотекой функций межпроцессорного обмена сообще-

ниями и содержит около 300 функций, которые делятся на следующие классы:

операции точка-точка, операции коллективного обмена, топологические опера-

ции, системные и вспомогательные операции. Поскольку MPI является стан-

дартизованной библиотекой функций, то написанная с применением MPI про-

грамма без переделок выполняется на различных параллельных ЭВМ. Принци-

пиально для написания подавляющего большинства программ достаточно не-

скольких функций, которые приведены ниже.

Функция MPI_Send является операцией точка-точка и используется для посылки данных в конкретный процесс.

Функция MPI_Recv также является точечной операцией и используется для приема данных от конкретного процесса.

Для рассылки одинаковых данных всем другим процессам используется коллективная операция MPI_BCAST, которую выполняют все процессы, как посылающий, так и принимающие.

Функция коллективного обмена MPI_REDUCE объединяет элементы входного буфера каждого процесса в группе, используя операцию op, и возвращает объединенное значение в выходной буфер процесса с номером root.

MPI_Send(address, сount, datatype, destination, tag, comm),

аddress – адрес посылаемых данных в буфере отправителя

сount – длина сообщения

datatype – тип посылаемых данных

destination – имя процесса-получателя

tag – для вспомогательной информации

comm – имя коммуникатора

MPI_Recv(address, count, datatype, source, tag, comm, status)

address – адрес получаемых данных в буфере получателя

count– длина сообщения

datatype– тип получаемых данных

source – имя посылающего процесса процесса

tag -для вспомогательной информации

comm– имя коммуникатора

status -для вспомогательной информации

MPI_BCAST (address, сount, datatype, root, comm)

root – номер рассылающего (корневого)процесса

MPI_REDUCE(sendbuf, recvbuf, count, datatype, op, root, comm)

sendbuf -адрес посылающего буфера

recvbuf -адрес принимающего буфера

count -количество элементов в посылающем буфере

datatype – тип данных

op -операция редукции

root -номер главного процесса

Кроме этого, используется несколько организующих функций.

MPI_INIT ()

MPI_COMM_SIZE (MPI_COMM_WORLD, numprocs)

MPI_COMM_RANK (MPI_COMM_WORLD, myid)

MPI_FINALIZE ()

Обращение к MPI_INIT присутствует в каждой MPI программе и должно

быть первым MPI – обращением. При этом в каждом выполнении программы

может выполняться только один вызов После выполнения этого оператора все

процессы параллельной программы выполняются параллельно. MPI_INIT.

MPI_COMM_WORLD является начальным (и в большинстве случаев единственным) коммуникатором и определяет коммуникационный контекст и связанную группу процессов.

Обращение MPI_COMM_SIZE возвращает число процессов numprocs, запущенных в этой программе пользователем.

Вызывая MPI_COMM_RANK, каждый процесс определяет свой номер в группе процессов с некоторым именем.

Строка MPI_FINALIZE () должно быть выполнена каждым процессом программы. Вследствие этого никакие MPI – операторы больше выполняться не будут. Перемсенная COM_WORLD определяет перечень процессов, назначенных для выполнения программы.

 

MPI программа для вычисления числа π на языке С.

Для первой параллельной программы удобна программа вычисления числа π, поскольку в ней нет загрузки данных и легко проверить ответ. Вычисления сводятся к вычислению интеграла по следующей формуле:

где xi = (i- 1/2 ) / n. Программа:

 

#include "mpi.h"

#include <math.h>

int main (int argc, char *argv[])

{

int n, myid, numprocs, i; /* число ординат, имя и число процессов*/

double PI25DT = 3.141592653589793238462643; /* используется для оценки

точности вычислений */

double mypi, pi, h, sum, x; /* mypi – частное значение π отдельного процесса, pi –

полное значение π */

MPI_Init(&argc, &argv); /* задаются системой*/

MPI_Comm_size(MPI_COMM_WORLD, &numprocs);

MPI_Comm_rank(MPI_COMM_WORLD,&myid);

while (1)

{

if (myid == 0) {

printf ("Enter the number of intervals: (0 quits) "); /*ввод числа ординат*/

scanf ("%d", &n);

}

MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);

if (n == 0) /* задание условия выхода из программы */

break;

else {

h = 1.0/ (double) n; /* вычисление частного значения π некоторого процесса */

sum = 0.0;

for (i = myid +1; i <= n; i+= numprocs) {

x = h * ((double)i - 0.5);

sum += (4.0 / (1.0 + x*x));

}

mypi = h * sum; /* вычисление частного значения π некоторого процесса */

MPI_Reduce(&mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0,

MPI_COMM_WORLD); /* сборка полного значения π */

if (myid == 0) /* оценка погрешности вычислений */

printf ("pi is approximately %.16f. Error is

%.16f\n", pi, fabs(pi - PI25DT));

}

}

MPI_Finalize(); /* выход из MPI */

return 0;

}