
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм автоматического распараллеливания арифметическихСодержание книги
Поиск на нашем сайте выражений (по А.В.Вальковскому)
Этот метод, использует отношение старшинства между операциями. Идея метода в том, что в выражении выделяются подвыражения, содержащие самые высокоприоритетные операции. Выделенные подвыражения одинаковой глубины «склеиваются» в более крупное подвыражение, таким образом «вырастает» выражение, все подвыражения которого имеют равномерную глубину. Обычно в качестве знаков арифметических операций используют: +, -, *, /,!,μ. Две последние операции — возведение в степень и унарный минус. При неформальном изложении знак умножения * иногда опускается. Вводится стар- шинство, или приоритет, операций:
Pr(μ) = 4; Pr(!) = 3; Pr(*) = Pr(/) =2; Pr(+) = Pr(-) = 1.
Опишем один вариант алгоритма более подробно, используя для наглядности только лишь выражения с операциями +, *. Для хранения текущей информации нам потребуется следующая память: ячейки х — для сканируемых операндов, у — для сканируемых операций, L — для операции, стоящей слева от текущего операнда, R — для аналогичной опе- рации справа, Out — для выходного выражения, Т i — ячейки для записи про- межуточных результатов. Кроме того, воспользуемся вектор-стеком: St = (St1, St2) — компонента St1 для операндов; St2 — для операций; Sc — процедура сканирования следующего символа входной строки; символ —> обозначает за- сылку. Считается, что входное выражение слева и справа ограничено пробелами, Рг (▬) = 0. Первоначально в R и Out содержится пробел. Шаг 1. Sc —> х, Sc—> у, R —> L, у — > R. Сканируется очередной опе- ранд и знак операции после него. Операция (пробел) слева от операнда х засы- лается в ячейку L, справа от x — в ячейку R. Шаг 2. Если ( St = O OR Рг (L) < Рг (R) OR Рг (St2)<Рг (L) ) AND Рг (R)≠ O, то на шаг 3, иначе на шаг 4. Шаг 3. х —> St1, y —> St2, переход на шаг1. Запоминаем операнд и операцию и переходим к сканированию следующей пары (операнд, операция). Шаг 4. Если Рг (L) = Рг (St2), то на шаг 5, иначе на шаг 6. Шаг 5. Out Tk у —> Out. Если Pr (y) = 0, то конец разбора, иначе па шаг 1. Здесь промежуточная ячейка Тk = (St1 St2 x). Таким образом, когда найдены две операции одного старшинства, первая из них с соседними операндами группируется в промежуточный результат Tk, вслед за ним выписывается вторая операция, и все это приписывается к выходной строке. Далее Tk воспринимается алгоритмом как атомный операнд. Шаг. 6. Out х у —> Out, если у = "_", то конец разбора, иначе на шаг. 1. В случае если не находится двух операций одного старшинства и приоритеты пошли на убывание, операнд и операция просто приписываются к выходной строке. Приведенный алгоритм описывает один из проходов, после которого неко торые из подвыражений «свертываются» в промежуточные результаты Т k. По- сле этого алгоритм повторяется до тех пор, пока все выражение не сведется к единственному Tk. Покажем выражение е = а + b + с * d* I* f + g после серии последо- вательных проходов. 1. Входная строка: ▬ а + b +c*d*l*f+g ▬. 2. Результат 1-го прохода: ▬ T1 + T2 * Т3 + g ▬, где T1 = (а + b), T2 = (с*d), Т3 = (1 *f). 3. Результат 2-го прохода: ▬ T4 + Т5 ▬, где T4 = (T2 * T3), T5 = (T1 + g). 4. Результат 3-го прохода: ▬T6 ▬; T6 = (T4 + T5). 5. Выходная строка: ▬ (((с * d) * (l * f)) + ((а + b ) + g)) ▬ Представим таблицу, подробно описывающую весь процесс преобразования указанного выражения.
Дерево выходного выражения (ЯПФ, полученная на основе сравнения старшинства операций)

Доказано, что описанный алгоритм дает в результате выражение с мини- мальным временем выполнения. Однако он имеет ряд существенных недостат- ков, главный из которых—многопроходность: он требует столько проходов, ка- ково время выполнения сгенерированного выражения. Чтобы избавиться от многопроходности, нужно в процессе разбора «нести» попутно информацию об уровне формируемых конструкций. Имеется однопроходная версия метода.
Алгоритм распараллеливания программы базового блока. Построение ЯПФ для отрезка программы производится путем определения зависимости пар смежных команд при анализе программы сверху вниз согласно алгоритму на рисунке.(l – промежуточная переменная, i – номер команды в программе)
ЛЕКЦИЯ 7. Планирование ЯПФ базовых блоков. Спланировать – означает указать, на каком процессоре и в каком такте будет запущен на исполнение некоторый блок вычислений. Алгоритмы планирования связаны с природой графа управления: состоит ли он из одного или нескольких базовых блоков, является ли граф управления циклическим или ациклическим графом в случае нескольких базовых блоков. Алгоритмы для одиночных базовых блоков называются локальными, остальные – глобальными. Алгоритмы ациклического планирования связаны с графами управления, которые не содержат циклов, или, что более типично, с циклическими графами, для которых существует самостоятельное управление на каждой обратной дуге графа управления.
Метод списочных расписаний. Планирование для единичного ББ заключается в построении как можно более короткого плана. Поскольку эта проблема имеет переборный характер, внимание было сосредоточено на эвристических алгоритмах планирования. Среди таких алгоритмов наиболее подходящими оказались списочные расписания. Алгоритмы планирования по списку при линейном росте времени планирования при увеличении числа планируемых объектов, дают результаты, отличающиеся от оптимальных всего на 10-15%. В таких расписаниях оператором присваиваются приоритеты по тем или иным эвристическим правилам, после чего операторы упорядочиваются по убыванию или возрастанию приоритета в виде линейного списка. В процессе планирования затем осуществляется назначение операторов процессорам в по- рядке их извлечения из списка. На рисунке (а) представлена исходная ЯПФ. Номера вершин даны внутри кружков, а время исполнения — около вершин. На рисунке (б) приведены уровни вершин. Под уровнем вершины понимается длина наибольшего пути из этой вершины в конечную. Построим для примера два расписания из множества возможных. Для каждого из них найдем характеристики всех вершин по соот ветствущим алгоритмам и примем значения этих характеристик в качестве ве- личин приоритетов этих вершин. В первом расписании величина приоритета вершины есть ее уровень. Это расписание УР. Во втором расписании величина приоритета вершины есть ее уровень без учета времени исполнения, то есть здесь веса всех вершин полага- ются одинаковыми (единичными).
б) Приоритеты и списки вершин (П— приоритеты, В — номера вершин) в) Уровни вершин
г) Реализация расписаний (Р1, Р2 — процессоры, X — простой процессора)
УР (по уровню вершин)
УР без учета веса вершин
Об оптимальности расписания можно судить по количеству простоев про- цессоров. Первое расписание дает 2, второе — 5.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |




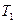 +
+

 *
*
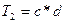
 +
+
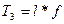
 +
+
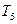
 ▬
▬






